变分推断(VI)、随机梯度变分推断(SGVI/SGVB)、变分自编码器(VAE)串讲

参考资料：

• VI参考：PRML Chapter 10.
• SGVI原文：Auto-Encoding Variational Bayes -- Kingma.
• VAE参考1：Tutorial on Variational Autoencoders -- CARL DOERSCH.
• VAE参考2：Stanford University CS236: Deep Generative Models.

泛函和变分法

本章主要是了解："变分"这个名称是怎么来的。

函数和泛函

• 函数：值到值的映射；
• 泛函：函数到值的映射。

一个典型的泛函 —— 熵的表达式：

\[H[p] = \int p(x) \ln p(x) \text{d}x
\]

• 函数的导数：输入值发生极小变化时，输出值的变化。
• 泛函的导数：输入函数发生极小变化时，输出值的变化。

泛函的极值

• 求泛函的极值：遍历所有可能的函数，来找到最大化或者最小化泛函的那个函数。
• 变分法：研究泛函极值的方法。
• 在VI中，将隐变量模型的推断问题转化成了求泛函极值的问题，所以称它们是"变分"。

变分推断VI

本章讨论一种近似推断方法 -- 变分推断。

问题 -- 推断隐变量模型的Posterior和Evidence

符号表示

• \(Z\)：隐变量，可以包括模型参数。
• \(X\)：观测数据，显变量。
• \(P(Z)\)：隐变量的先验概率，在这个问题中是已知的。
• \(P(X\mid Z)\)：隐变量的似然概率，在这个问题中是已知的。
• \(P(X,Z)\)：联合概率，可以直接\(P(X,Z)=P(X\mid Z)P(Z)\).
• \(P(Z \mid X)\)：隐变量的后验概率，是需要求出来的。
• \(P(X)\)：Marginal Evidence (或者就称作Evidence)，是需要求出来的。

Tractable和Intractable

Tractable

典型例子如隐马尔可夫模型 (HMM)，其主要特点：

• 只有有限个隐状态。
• 模型的结构简单。

所以模型参数已知时，可以直接用基于动态规划的精确推断方法：

• 求\(P(X)\)：前向反向算法。
• 求\(P(Z\mid X)\)：维特比算法。

---

Intractable

但是很多情况下：

• 涉及对连续随机变量积分。
• 模型结构很复杂。

此时想要精确推断通常intractable. 主要的困难就在于积分：\(P(X) = \int P(X,Z)\text{d}Z\).

因此需要使用近似推断方法。接下来介绍的是一种近似推断方法 —— 变分推断。

ELBO的推导

考虑贝叶斯公式，在等式两边加上\(\log\)：

\[\log P(X) = \log \frac{P(X,Z)}{P(Z|X)} =\log P(X,Z) -\log P(Z\mid X)
\]

引入一个由\(\phi\)参数化的概率分布\(q_\phi(Z)\):

\[\begin{aligned}
\log P(X) &= \log P(X,Z) -\log P(Z\mid X) \\
&= \log \frac{P(X,Z)}{q_\phi(Z)} - \log \frac{P(Z\mid X)}{q_\phi(Z)}
\end{aligned}
\]

等式两边同时对分布\(q_\phi(Z)\)求均值，可以得到：

\[\int_Z \log P(X) q_\phi(Z) \text{d} Z = \int_Z q_\phi(Z) \log \frac{P(X,Z)}{q_\phi(Z)}\text{d} Z - \int_Z q_\phi(Z) \log \frac{P(Z\mid X)}{q_\phi(Z)} \text{d}Z
\]

由于左边\(\log P(X)\)和\(Z\)无关，可以直接提出来，又\(\int_Z q_\phi(Z) \text{d}Z =1\)，所以有：

\[\log P(X) = \int_Z q_\phi(Z) \log \frac{P(X,Z)}{q_\phi(Z)}\text{d} Z - \int_Z q_\phi(Z) \log \frac{P(Z\mid X)}{q_\phi(Z)} \text{d}Z
\]

将等式右边的第一项写成期望形式，第二项可以写成KL divergence的形式：

\[\begin{aligned}
\log P(X)&= \mathbb E_{Z\sim q_\phi} [\log P(X,Z) - \log q_\phi(Z)] + KL(q_\phi(Z) \mid\mid P(Z\mid X))
\end{aligned}
\]

观察这个式子，注意到以下性质：

• 由于\(KL\ge 0\)，所以总有\(\log P(X) \ge \text{第一项}\)，即第一项是\(\log\) Evidence的下界，简称为\(ELBO\) (Evidence Lower BOund).
• 当且仅当\(q_\phi(Z) = P(Z\mid X)\)时，\(KL=0\)，此时\(\log P(X) = ELBO\).
• KEY1：因此只需要找出\(\arg \max_{q_\phi}ELBO\)，就可以使得\(ELBO\to \log P(X)\)，同时会有\(KL \to 0\)，此时就有\(q_\phi(Z) \to P(Z\mid X)\).
• KEY2：一句话概括变分推断，就是将隐变量模型的推断问题转化成了最优化\(ELBO\)的问题。

---

REMARK1：把\(ELBO\)看作一个泛函\(\mathcal L(q_\phi)\)，目标就是\(\arg \max_{q_\phi} \mathcal L(q_\phi)\)，即求泛函的极值点 (所以叫变分)。

REMARK2：变分法天生不是近似方法，因为假如真的能够考虑到所有可能的函数，那就一定可以精确推断到后验概率。但是由于我们通常会对函数的范围做出假定，比如函数是二次型、或者函数满足平均场分解的条件，这导致了最后得出来的总是近似解。

REMARK3：还有一种基于平均场理论的对\(q(z)\)的假定，在此基础上可以利用坐标上升法求最优解，详情可以参考PRML Chapter10.

如果考虑单个样本

• \(X=\{x^{(1)},...,x^{(n)}\}\)：观测变量。
  
  假定每个样本独立同分布，则\(P(X)\)可以拆成连乘：

\[\log P(X) = \log \prod P(x^{(i)}) = \sum \log P(x^{(i)})
\]

引入一个由\(\phi^{(i)}\)参数化的分布\(q_{\phi^{(i)}}(Z\mid x^{(i)})\)，\(\log P(x^{(i)})\)同样可以写成\(ELBO+KL\)的形式：

\[\begin{aligned}
\log P(x^{(i)}) &= \int_Z q_{\phi^{(i)}}(Z\mid x^{(i)}) \log \frac{P(x^{(i)},Z)}{q_{\phi^{(i)}}(Z\mid x^{(i)})}\text{d} Z - \int_Z q_{\phi^{(i)}}(Z\mid x^{(i)}) \log \frac{P(Z\mid x^{(i)})}{q_{\phi^{(i)}}(Z\mid x^{(i)})} \text{d}Z \\
&= \mathbb E_{Z\sim q_{\phi^{(i)}}} [\log P(x^{(i)},Z) - \log q_{\phi^{(i)}}(Z\mid x^{(i)})] + KL(q_{\phi^{(i)}}(Z\mid x^{(i)}) \mid\mid P(Z\mid x^{(i)})) \\
&= ELBO +KL
\end{aligned}
\]

NOTE：\(q_\phi\)的参数\(\phi\)写作\(\phi^{(i)}\)，是因为对于每单个观测变量来说，后验\(P(Z\mid x^{(i)})\)是不一样的。之后[[#SGVI]]章节中，为了表示简单，依然省略不写。

SGVI

上一章把隐变量的推断问题转化为了最优化\(ELBO\)问题，本章节讲估计\(ELBO\)梯度的方法。

• SGVI即随机梯度(stochastic gradient)变分推断，使用基于梯度的优化方法来最大化\(ELBO\).
• 求出梯度之后，\(q_\phi(z)\)参数更新：\(\phi = \phi + \alpha \nabla_\phi ELBO\).

Score function gradient estimator

\(ELBO\)对\(\phi\)的梯度形如\(\nabla_\phi \mathbb E_{z\sim q_\phi(z)}[f(z)]\)，下面先分析这个更一般化的形式的梯度：

\[\nabla_\phi \mathbb E_{z\sim q_\phi(z)}[f(z)] = \nabla_\phi \int q_\phi(z) f(z) \text{d}z
\]

把梯度符号移入积分号，然后由于\(\nabla \log q_\phi=\frac{\nabla q_\phi}{q_\phi}\)，可得：

\[\begin{aligned}
\nabla_\phi \mathbb E &= \int \nabla_\phi q_\phi(z) f(z) \text{d}z \\
&= \int q_\phi(z) \nabla_\phi \log q_\phi(z) f(z) \text{d}z \\
&= \mathbb E_{z\sim q_\phi(z)}[f(z) \nabla_\phi \log q_\phi(z)]
\end{aligned}
\]

等式右边的期望可以直接使用MC采样来估计：

\[\mathbb E_{z\sim q_\phi(z)}[f(z) \nabla_\phi \log q_\phi(z)] \approx \frac{1}{L} \sum_{l=1}^L f(z^{(l)}) \nabla_\phi \log q_\phi(z^{(l)})
\]

• \(z^{(l)}\sim q_\phi(z)\).
• 这个估计方法被称作score function gradient estimator，其中\(\nabla_\phi \log q_\phi(z)\)被称作是score，\(f(z)\)被称作是cost.
• 这个estimator存在的问题是：方差太大，很多时候都用不了，也不适合直接拿来估计\(ELBO\).

NOTE：我们实际上假定了\(q_\phi(z)\)是tractable的，既容易采样又容易计算。

BTW：强化学习中的REINFORCE算法中，估计策略梯度用的就是这个estimator，所以我们会说REINFORCE是一种方差很大的算法。

Reparameterized trick

采样过程\(z\sim q_\phi(z\mid x)\)，通常可能分解成以下两个步骤：

1. 先从一个noise分布中采出\(\epsilon \sim p(\epsilon)\).
2. 然后找出一个由\(\phi\)参数化的函数\(g_\phi(,)\)，使得\(z=g_\phi(\epsilon, x)\).

比如说从正态分布采样\(z\sim \mathcal N(\mu, \sigma)\)，就可以拆分成：

1. \(\epsilon \sim \mathcal N(0,1)\).
2. \(z = \mu + \epsilon \sigma\).

以上就是重参数化技巧。

SGVI estimator

在使用重参数化技巧之后，可以把期望的表达式写成以下形式：

\[ \mathbb E_{z\sim q_\phi(z\mid x^{(i)})}[f(z)]=\mathbb E_{\epsilon \sim p(\epsilon)}[f(g_\phi(\epsilon, x^{(i)}))] \approx \frac{1}{L} \sum_{l=1}^L f(g_\phi(\epsilon^{(l)},x^{(i)}))
\]

令\(f=ELBO\)，再求梯度，就得到了SGVI estimator：

\[\nabla_\phi ELBO=\nabla_\phi \mathcal L(\phi,x^{(i)}) = \nabla_\phi \bigl(\frac{1}{L}\sum_{l=1}^L \log P(x^{(i)},g_\phi(\epsilon^{(l)},x^{(i)})) - \log q_\phi(g_\phi(\epsilon^{(l)},x^{(i)})\mid x^{(i)}) \bigr)
\]

其中\(\epsilon^{(l)}\sim p(\epsilon)\).

NOTE：SGVI estimator通常会比score function gradient estimator有更小的方差。

变分自编码器VAE

本章讨论VI方法是如何应用到隐变量生成模型的推断和学习中的。

样本的分布

我们常常希望生成和数据集中的数据相似的样本。比如说给一个人脸数据集，我们希望模型能够通过某种方式学习这批人脸数据的分布，然后能够再通过某种方式生成出人脸来。

• 对样本的假定：通常会假定数据集是从一个未知分布\(P_{gt}(X)\)采样出来的.

• 理解：如果一张图片\(X\)有人脸的样子，那么\(P_{gt}(X)\)就很大；如果一张图片\(X\)都是噪声，那么\(P_{gt}(X)\)就很小。

• 我们的目的：找到一个可以采样的模型\(P(X)\)，同时\(P\)能够尽可能逼近\(P_{gt}\).

• 如何学习模型参数：假设参数化的模型\(P_\theta(X)\)，要学习参数\(\theta\)，就是要让模型在已经观测到的数据\(X\)上，概率最大，即：\(\arg \max_\theta P_\theta(X)\) (Max Likelihood).

隐变量生成模型

考虑使用隐变量生成模型来逼近\(P_{gt}\).

引例：以生成数字为例，一种思考方法

1. 模型先确定\({0,1,...,9}\)范围的一个数字\(z\).
2. 然后再基于\(P(X\mid z;\theta)\)从\(z\)生成对应数字的图片。

这里的\(z\)就是隐变量。

---

困难：确定隐变量，再确定隐变量和观测变量的关系，这个过程实际上可能很复杂：

• 比如模型可能要先确定要生成的数字里有没有圆圈 (0, 8, 9)，再确定圆圈的数量。
• 除此之外，还可能需要确定数字的倾斜度、字体等更复杂的关系。

---

考虑用如下方法来克服：

1. 直接假定隐变量服从高斯先验分布\(z \sim \mathcal N(0,I)\).
2. 假定模型也是一个高斯分布\(P(X\mid z;\theta)=\mathcal N(X\mid \mu_\theta(z),\sigma_\theta(z))\)，其参数是关于\(z\)的函数。
3. 参数\((\mu_\theta(z), \sigma_\theta(z))\)都使用神经网络来建模。

为什么这样做：

• KEY1：简单的高斯分布，经过足够复杂的非线性变换，就可以表示出任意的分布。
• KEY2：由于神经网络可以建模任意复杂的非线性关系，所以最后可以表示出任意我们想要的分布。
• Example：对高斯分布做非线性变换。左边是高斯分布，右边是\(g(z) = \frac{z}{10} + \frac{z}{||z||}\).
  
  

---

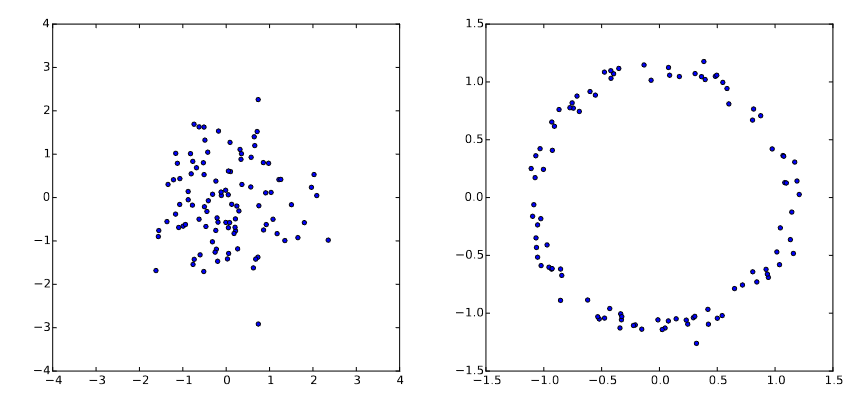
因此得到我们用来近似真实数据分布\(P_{gt}(X)\)的模型\(P(X;\theta)\)：

\[P(X;\theta) = \int P(X,z;\theta)\text{d}z =\int P(X\mid z;\theta) P(z) \text{d}z =\int \mathcal N(X\mid \mu_\theta,\sigma_\theta) \mathcal N(0,I)\text{d}z
\]

• 可以认为这个模型的表示能力是足够的。
• \(z\)对我们来说是不可观测的隐变量，所以需要考虑所有可能\(z\) (体现在积分).
• 是很复杂的模型，推断模型的Marginal Evidence \(P(X;\theta) = \int P(X,z;\theta)\text{d}z\)、学习模型参数\(\arg \max_\theta P(X;\theta)\)，都很困难。

模型的近似推断和学习

考虑使用变分推断的近似方法。

根据[[#变分推断VI]]部分的讨论，可以将模型的\(\log\) Evidence写成\(ELBO+KL\)的形式：

\[\begin{aligned}
\log P(x^{(i)};\theta) &= \mathbb E_{z\sim q_{\phi^{(i)}}} [\log P(x^{(i)},z;\theta) - \log q_{\phi^{(i)}}(z)] + KL(q_{\phi^{(i)}}(z) \mid\mid P(z\mid x^{(i)};\theta))
\end{aligned}
\]

主要区别：带上了模型参数\(\theta\).

NOTE：现在最大化\(ELBO\)，既需要考虑近似分布\(q\)的参数\(\phi\)，也需要考虑模型参数\(\theta\).

NOTE：此时，最大化\(ELBO\)同时具有两个作用：

1. 推断：最小化了\(KL\)，使得\(q\)逼近真实后验分布；

2. 学习：最大化了Evidence，相当于做了MLE，使得模型\(P_\theta\)逼近真实数据分布\(P_{gt}\).

再根据[[#SGVI]]部分的讨论，使用SGVI estimator来估计\(ELBO\)：

\[\nabla \mathcal L(x^{(i)},\phi^{(i)},\theta)=\nabla \bigl(\frac{1}{L}\sum_{l=1}^L \log P(x^{(i)},g_{\phi^{(i)}}(\epsilon^{(l)},x^{(i)});\theta) - \log q_{\phi^{(i)}}(g_{\phi^{(i)}}(\epsilon^{(l)},x^{(i)})) \bigr)
\]

• \(g_\phi(\epsilon^{(l)},x^{(i)})\)是重参数化后的\(z\).
• \(\epsilon \sim p(\epsilon)\).
• 梯度算子\(\nabla = \{\nabla_\phi, \nabla_\theta\}\).

讨论至此，可以得到模型的学习过程如下：

Amortized Inference

• 上方学习过程的一个缺点：对于每个\(x\)，都要先推断出一个足够好的\(q_{\phi^*}\).
• KEY：近似推断后验概率 = 学习后验概率的参数 (这个视角是由VI提供的)。

Amortized Inference：考虑引入一个参数化的函数\(f_\lambda: x^i \to \phi^*\)，它会学习如何根据\(x^i\)确定一个足够好的\(\phi^*\). 即对于每个\(x^i\)，都会得到后验\(q(z;f_\lambda(x^i))\).

如何学习？同样是重参数化+梯度上升。

因此，得到更简化的模型学习过程：

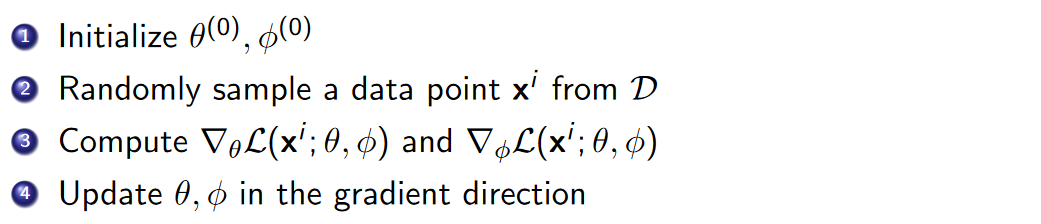
NOTE：直到[[#Amortized Inference]]这一小节截止，才开始有了Encoder-Decoder结构的雏形，即\(x^i\to q(z;f_\lambda(x^i)) \to z \to P(X\mid z;\theta) \to \bar x^i\).

对Objective的解析

训练VAE是以最大化\(ELBO\)为目标，这一小节从\(ELBO\)本身的形式，讨论\(ELBO\)的实际意义。

这里推导用的是符号简化版的\(ELBO\)表达式：

\[\begin{aligned}
ELBO &= \int q_\phi(Z)\log P(X,Z) - q_\phi(Z)\log q_\phi(Z) \text{d}Z \\
&= \int q_\phi(Z)\log P(X\mid Z) + q_\phi(Z) \log P(Z) - q_\phi(Z)\log q_\phi(Z) \text{d}Z \\
&=\int q_\phi(Z)\log P(X\mid Z) + q_\phi(Z) \log \frac{P(Z)}{q_\phi(Z)}\text{d}Z \\
&= \int q_\phi(Z)\log P(X\mid Z) \text{d}Z + \int q_\phi(Z) \log \frac{P(Z)}{q_\phi(Z)}\text{d}Z \\
&=\mathbb E_{q_\phi}[\log P(X\mid Z)] - KL(q_\phi(Z)\mid\mid P(Z))
\end{aligned}
\]

可以看到\(ELBO\)两项的意义：

1. 第一项：可以看作是Loss项，意义是极大似然，表示我们想要生成的\(X\)和数据集尽可能相似。
2. 第二项：可以看作是正则化项，意义是希望后验尽可能接近已知的先验\(P(Z)\)，这表明我们想要从\(P(Z)\)随机抽一个\(z\)，就大概率能生成有意义的结果。

VAE结构示例

下面是由前馈神经网络实现Encoder、Decoder的VAE的结构示意图。左图是无重参数化技巧的，右图是有重参数化技巧的。

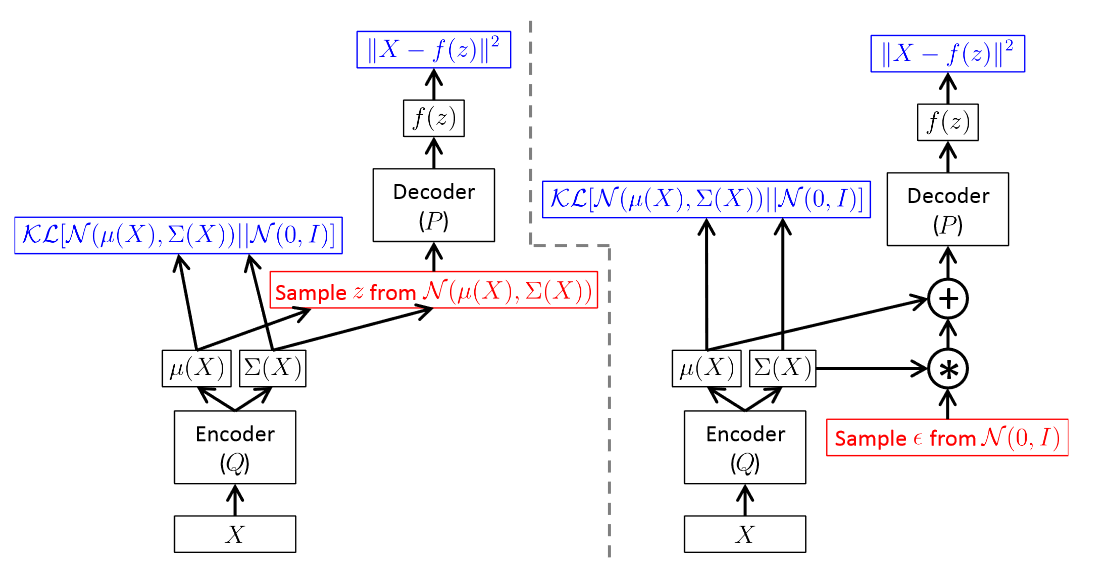
几个要点：

• 网络输出：Decoder从隐变量\(z\)重建\(\bar X\)；Encoder输出\(q_\phi(z\mid X)\)，即从\(X\)压缩到隐变量。
• 重参数化和Autodiff：重参数化技巧使得autodiff可以将误差从Decoder一直传回到输入。
• Objective的选择：不必严格是\(ELBO\)
  1. Loss项：要能体现Reconstruction error，根据问题的不同可以灵活选择。
  2. 正则项：除了KL散度外，也可以采用其他的散度。
• 关于生成：Decoder部分才是我们的隐变量生成模型。随机从\(\mathcal N(0,I)\)中抽取\(z\)，再输入到Decoder中，就可以生成样本。

参考代码

以下是基于CNN的VAE实现。

Encoder

class Encoder(nn.Module):
    def __init__(self, num_channels, hidden_size):
        super(Encoder, self).__init__()
        # 输入是(batch_size, num_channels, 28, 28)，就是MNIST数据集的形状
        self.conv1 = nn.Conv2d(num_channels, 32, 4, 2) # (28 - 4) / 2 + 1 = 13
        self.conv2 = nn.Conv2d(32, 64, 4, 2, 1) # (13 - 4 + 1) / 2 + 1 = 6
        self.conv3 = nn.Conv2d(64, 128, 4, 2) # (6 - 4) / 2 + 1 = 2

        self.fc_mu = nn.Linear(128 * 2 * 2, hidden_size)
        self.fc_logstd = nn.Linear(128 * 2 * 2, hidden_size)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        x = torch.flatten(x, start_dim=1)
        mu = self.fc_mu(x)
        log_std = self.fc_logstd(x)
        return mu, log_std

Decoder

class Decoder(nn.Module):
    def __init__(self, num_channels, hidden_size):
        super(Decoder, self).__init__()

        self.fc1 = nn.Linear(hidden_size, 512)
        self.deconv1 = nn.ConvTranspose2d(512, 64, 5, 2)
        self.deconv2 = nn.ConvTranspose2d(64, 32, 5, 2)
        self.deconv3 = nn.ConvTranspose2d(32, num_channels, 4, 2)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = x.unsqueeze(-1).unsqueeze(-1) # num -> [[num]]
        x = F.relu(self.deconv1(x))
        x = F.relu(self.deconv2(x))
        reconstruction = F.sigmoid(self.deconv3(x)) # output (0, 1)
        return reconstruction

VAE

class VAE(nn.Module):
    def __init__(self, num_channels, hidden_size):
        super(VAE, self).__init__()
        self.encoder = Encoder(num_channels, hidden_size)
        self.decoder = Decoder(num_channels, hidden_size)

    def forward(self, x):
        mu, log_std = self.encoder(x)
        z = self.reparameterize(mu, log_std)
        reconstruction = self.decoder(z)
        return reconstruction, mu, log_std

    def reparameterize(self, mu, log_std):
        std = log_std.exp()
        eps = torch.randn_like(std)
        return mu + std * eps

Loss

def vae_loss(x, reconstruction, mu, log_std):
	# 图像生成，使用BCE的效果会比较好
    rec_loss = F.binary_cross_entropy(reconstruction, x, reduction='sum')
    # 这里是化简后的q和N(0, I)的KL散度表达式
    kl_loss = -0.5 * torch.sum(1 + 2 * log_std - mu.pow(2) - (2*log_std).exp())
    return rec_loss + kl_loss