2025dsfz集训Day7: KMP与Trie树

Day7: KMP与Trie树

\[Designed\ By\ FrankWkd\ -\ Luogu@Lwj54joy,uid=845400
\]

特别感谢 此次课的主讲 - Kwling

KMP算法

• \(KMP (Knuth–Morris–Pratt)\) 是一个字符串匹配算法，于1977年由上述三人共同发表。
  
  在线性的时空复杂度内解决字符串匹配。

字符串匹配

• 给定两个字符串 \(s,t\)（通常来讲我们管较短的串叫做“模式串”，长的叫“匹配串”。我们的任务是在长串内找到短串）。

• 我们定义记号 \(s[l,r]\) 表示的是 \(s\) 串，从下标 \(l\) 到下标 \(r\) 的子串。（比如说 \(s=“abcabca”\),那么 \(s[2,4]=“bca”，1-index\)）

• 字符串匹配：我们希望对于 s（长串）的每一个前缀 s[1,i]，找到最大的 j 使得 s[i-j+1,i]=t[1,j]

• 例：\(s=“ababc”,t=“aba”:\)
  
  \(i=1: s[1,1]=t[1,1]=“a” ; i=2:\) \(s[1,2]=t[1,2]=“ab”\)
  
  \(i=3: s[1,3]=t[1,3]=“abc”\)（成功匹配）； \(i=4: s[3,4]=t[1,2]=“ab”\)
  
  \(i=5: s[6,5]=t[1,0]=\phi\)  (未成功匹配，空串）

解法

• 我们希望能够复用尽量多的信息。
• 假设我们此时知道 \(s[1,i]\) 对应的匹配长度 \(k_i\)，怎么求出 \(s[1,i+1]\) 的匹配长度？
• 大致思路：先看看 \(s[i+1]\) 和 \(t[k_i+1]\) 一不一样。
  • 一样：长度++
  • 不一样：模式串前移 \(1\) 位

Border串

• 我们注意到，实际上我们是在找 \(t[1,j]\) 的一个既是其前缀又是其后缀的最长的子串。（当然需要不是 \(t[1,j]\) 本身）

• \(s=“abab”\) 那么 \(s[1,2]=“ab”\) 就是这样的串。
  
  即是前缀又是后缀串的名字是：\(border\) 串。

• 我们可以发现 \(border\) 集合：\(S_i=S_k+{k}\) ( \(k\) 是 \(t[1,i]\) 的最长border)。

  • 例：\(BS(“ababa”)={“a”,“aba”}=BS(“aba”)+{“aba”}\)
    
    其中 \(BS\) 是 \(border\ set\) 的意思（即所有的 \(border\) 串构成的集合）

• 这实际上也就是说：\(border\) 集合实际上是一条链

• 我们不断地去找串 \(S\) 的最长 \(border T\)，然后把他加入集合，把 \(S\) 变成 \(T\) 直到 \(S\) 为空。

• 现在问题变为：如何求出最长 \(border\)?

• 假设我们知道了 \(s[1,i]\) 的 \(border\)，怎么求出 \(s[1,i+1]\) 的 \(border\) 长度？
  
  我们不断地“跳” \(t[1,i]\) 的 \(border\) 来找到 \(t[1,i+1]\) 的 最长 \(border\)。

复杂度

• 看起来是 \(O(n^2)\) 的，但实则不然。

• 考虑每次最多让 \(border\) 链 变长 \(1\) ，以 \(border\) 链 长度作为“势能”，便可以分析出 \(O(n)\) 的摊还复杂度。

• 另一边的字符串匹配亦是同理。（算法，复杂度分析）

• 假设 \(s[i-j+1,i]\) 匹配到了 \(t[1,j]\)。

  • 我们不断地去 “跳” \(t[1,j]\) 的 \(border\)，找到一个 \(t[1,k]\) 使得 \(t[k+1]=s[i+1]\)。
  • 这样就完成了一次字符串匹配。

• 我们不难分析出，字符串匹配的复杂度为：\(O(n+m)=O(|S|+|T|)\)

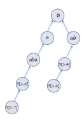
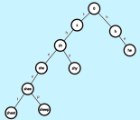
• 不难发现，实际上 border 集合的结构，可以用一颗树来描述。

• 以 S=“abababa” 举例。

  • \(S[1,1]\) 对应最长 \(border=\phi；\)
  • \(S[1,2]\) 对应最长 \(border=\phi 。\)
  • \(S[1,3]\) 对应最长 \(border=“a”；\)
  • \(S[1,4]\) 对应最长 \(border=“ab”。\)
  • \(S[1,5]\) 对应最长 $border=“aba”; $
  • \(S[1,6]\) 对应最长 \(border=“abab”。\)
  • \(S[1,7]\) 对应最长 \(border=“ababa”。\)

• 如图，这棵树具有很优良的性质。
  
  

• 可以发现，我们求解border的算法实际上不过是在 这棵树上进行 dfs。

Trie树

• 我们有这样一个“数据结构”能够去“维护”给定的“串集合” \(S\)。并且能支持“查询”一个串在不在这个“串集合” \(S\) 中。（￥S$ 即为字典）
• 很好理解，如图所示：假设字典 \(S={“she”,“he”,“shy”,“sheep”,“sheet”}\)
  • 那么字典树将如图所示：
    
    
  • 每一条边对应一个字母，每一个结点对应一个单词的前缀。
  • \(0\) 结点的含义是空串。
• 查询就是从 \(0\) 开始查找有没有对应字母的出边。

01Trie树

• \(0-1\)字典树可以很方便的维护形如“最大异或值”这类位运算查询。
• 我们将一个 \(32/64\) 位整数看成一个长为 \(32/64\) 的字符串。
• 例： \(4=(0…0100), 6=(0…0110), 11=(0…01011)\)，将他们插入 \(trie\) 中：
  • 特点：所有叶子等深。
• 假如我们想查询 \(x\) 与集合里的数最大异或值。
• 比如说 $x=8=(1000) $，我们从高往低按位考虑。
  • 在 \(root\) 处的出边是 \(1\)，我们看 \(root\) 有无 \(0\) 的出边，
  • 然后走向“结点 \(0\)”。（这样才能让异或值最大）
  • 接下来同理，我们在“结点 \(0\)” 看有没有 \(1\) 的出边……
    
    

题目&参考解法

• AccodersP2076 剪花布条
  
  思路： \(KMP\) 板子

#include<bits/stdc++.h>
using namespace std;
int nextl[1001]={0};//这个数组名不能直接用next,容易报错
string a,b;
int KMP(){
    int i=0,j=0,we=0;
    int as=a.size(),bs=b.size();
    while(i<as){
        if(a[i]==b[j]||j==-1){//当单个字符匹配成功或前面没东西
            i++;
            j++;//i,j都往前挪
            if(j==bs){//字符串匹配成功
                we++;
                j=0;//子串归0
            }
        }else{
            j=nextl[j];//上next数组，移动到下一个位置
        }
    }
    return we;
}
void Next(){//计算next数组值
    int bs=b.size();
    nextl[0]=-1;//代表前面没东西
    int j=0,k=-1;
    while(j<bs){
        if(k==-1||b[j]==b[k]){//当前面没有东西或j、k对应的字符一样
            nextl[j++]=k++;//直接往后挪一位，因为前几位字符=后几位字符或前面啥也没有
        }else{
            k=nextl[k];
        }
    }
}
int main(){
    while(cin>>a){
        if(a=="#"){
            break;
        }else{
            cin>>b;
            Next();
            cout<<KMP()<<endl;
        }
    }
}