牛客多校10 D Rikka with Prefix Sum 不是数据结构

https://www.nowcoder.com/acm/contest/148/D

题意：

1e5个数，1e5个操作，操作分为：

1、区间加。

2、整个数列替换为前缀和。

3、区间查询。 查询数小于500.

题解：比赛时的思路是：（基本正确，没能实现）

1.对于某个操作1，记录下其之后操作2的个数，就可以通过组合数O（1）算出该区间的每个数最终的结果。

2.各个操作1相互独立，分开来算，最后相加。（暴力出来的规律）

没想到的两点：

1.可以通过组合数O（1）算出区间和：用公式

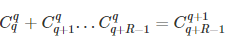
之前碰到过，杨辉三角上很明显。但直接导致我认为这个想法还是O(n*n/2)orz。

2.考虑某次区间加之后，操作2对该区间后面的数的影响：可以认为l~n加了v，r+1到n加了-v 正好抵消

另外：尝试了快速mod模板

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#include<map>
#include<string>
#include<bitset>

#define re register
#define rep(i,s,t) for(re int i=s;i<=t;++i)
#define per(i,s,t) for(re int i=s;i>=t;--i)
#define mmm(f,x) memset(f,x,sizeof f)
//#define x first
//#define xx second
using namespace std;

typedef  long long ll;

const ll mod = ;
template<typename T>inline void add_(T &A, int B, ll MOD = mod) { A += B; (A >= MOD) && (A -= MOD); }
template<typename T>inline void mul_(T &A, ll B, ll MOD = mod) { A = (A*B) % MOD; }
template<typename T>inline void mod_(T &A, ll MOD = mod) { A %= MOD; A += MOD; A %= MOD; }
const int maxn = 3e5 + ;
int a[maxn];
int n, m;
int tot,Q;
ll L[maxn], R[maxn],W[maxn],num2[maxn];
ll inv[maxn],  fac[maxn];
ll c[maxn];
long long kpow(long long a, long long n) {
    long long res = ;
    while (n > ) {
        if (n & )res = res * a%mod;
        a = a * a%mod;
        n >>= ;
    }
    return res;
}
void init() {
    fac[] = fac[] = ;
    inv[] = ;
    rep(i, , maxn) {
        fac[i] = fac[i - ] * (ll)i % mod;
        inv[i] = kpow(fac[i], mod - );
    }
}
ll C(int n, int m) {
    if (n < m) return 0ll;
    if (m ==  || n == m) return 1ll;
    if (n -  == m || m == ) return n;
    return fac[n] * inv[m] % mod * inv[n - m] % mod;
}
ll Csum(ll l, ll r, ll v, ll q) {
    if (l>r)return ;
    ll n = r - l + ;
    ll ans = v;
    mul_(ans,C(q + n - , q));
    mod_(ans);
    return ans;
}
ll query(int x) {
    ll ret = ;
    rep(i, , tot) {
        int q = Q - num2[i] + ;
        if (L[i] > x)continue;
        if (R[i] <= x) {
            add_(ret, Csum(L[i], x, W[i], q));
            add_(ret, Csum(R[i] + , x, -W[i], q));
            mod_(ret);
        }
        else add_(ret, Csum(L[i], x, W[i], q));
    }
    return ret;
}
int main() {
    init();
    int t;
    cin >> t;
    while (t--) {
        tot = ,Q=;
        cin >> n >> m;
        rep(i, , m) {
            int op;
            scanf("%d", &op);
            if (op == ) {
                Q++;
            }
            else {
                ll l, r;
                scanf("%lld%lld", &l, &r);

                if (op == ) {
                    ll w;
                    scanf("%lld", &w);
                    L[++tot] = l, R[tot] = r; W[tot] = w;
                    num2[tot] = Q;
                }
                else { cout<< (query(r) - query(l - ) + mod) % mod << endl; }
            }
        }
    }
}
/*
1
100000 7
1 1 3 1
2
3 2333 6666
2
3 2333 6666
2
3 2333 6666
*/