sicily 1119 Factstone Benchmark

题意：求满足n! < 2^k，n的最大值！

解题：指数比较转换成对数比较,达到降幂！

其中：　　log (n!) = log(n)+log(n-1)+...+log(1);

　　　　　　　　log(2^k) = k * log(2);

　　  当然也可以使用斯特林(stirling 公式求解)

公式如下：

　　　　　　　　

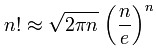
 程序代码：

 ============================================

 #include<iostream>
 #include<cmath>
 using namespace std;
 int main(){
  　　int year;
  　　double res;
  　　while(cin >> year && year >){
   　　　　//add 2 because of the beginning with 4, 1<<2 equals with 4
   　　　　int bits = <<((year -)/+);
   　　　　double i=;
   　　　　res =;
   　　　　while(res<bits){
    　　　　　　res += log(i)/log(double());
    　　　　　　i++;
   　　　　}
  　　　　 cout<<i-<<endl;
  　　}
  　　return ;
 }

 ============================================