如何优雅的使用C语言绘制一只小猪佩奇

今天我们来用C语言画一只小猪佩奇---社会、社会....
在画小猪佩奇之前，我们先使用带符号的距离长 (signed distance field,SDF) 来画一个圆形。

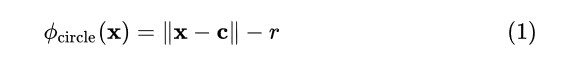
使用这个方法表示形状，但是这次我们使用 ASCⅡ 字符 \/=\ 画出形状的外框，并填充内部，类似这样：

  =====


//.....\\


||.....||


\\....//
   

  =====


SDF 的梯度（gradient）代表 SDF 变化最大的方向，可用这个方向去决定用哪一个字符。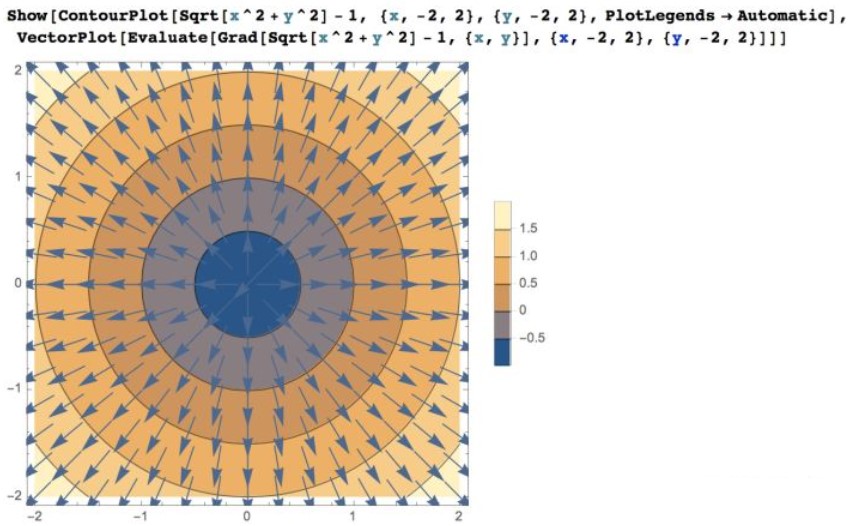

我们通过差分求 SDF 的梯度近似值，然后用 atan2() 求出梯度的角度：

用 C 语言简单实现，在 [-1, 1] x [-1, 1] 画布中画一个半径 0.8 并带有 0.1 宽度外框的圆形: 
#include <math.h>
#include <stdio.h>
#define T double

T f(T x, T y)
{
　　return sqrt(x x + y y) - 0.8f;
}

char outline(T x, T y)
{

　　 T delta = 0.001;
　　if (fabs(f(x, y)) < 0.05)
　　{
　　　　T dx = f(x + delta, y) - f(x - delta, y);
　　　　T dy = f(x, y + delta) - f(x, y - delta);
　　　　return "|/=\|/=\|"[(int)((atan2(dy, dx) / 6.2831853072 + 0.5) * 8 + 0.5)];
　　}
　　else if (f(x, y) < 0)
　　{
　　　　return '.';
　　}
　　else
　　{
　　return ' ';

　　}
}

int main()
{
　　for (T i = -1; i < 1; i += 0.05, putchar('\n'))
　　{
　　　　for (T j = -1; j < 1; j += 0.025)
　　　　{
　　　　　　putchar(outline(j, i));
　　　　}　

　　}
　　getchar();
　　return 0;
}

然后，我们就可以通过画多个圆形，把它们适当地旋转和缩放，用构造实体几何比它们组合起来，从而就可以画出小猪佩奇了：

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define T double

T c(T x, T y, T r)
{
　　return sqrt(x x + y y) - r;
}

T u(T x, T y, T t)
{
　　return x cos(t) + y sin(t);
}

T v(T x, T y, T t)
{
　　return y cos(t) - x sin(t);

}

T fa(T x, T y)

{

　　 return fmin(c(x, y, 0.5), c(x * 0.47 + 0.15, y + 0.25, 0.3));

}

T no(T x, T y)
{
　　return c(x * 1.2 + 0.97, y + 0.25, 0.2);
}

T nh(T x, T y)

{
　　

　　 return fmin(c(x + 0.9, y + 0.25, 0.03), c(x + 0.75, y + 0.25, 0.03));

}

T ea(T x, T y)
{
　　return fmin(c(x 1.7 + 0.3, y + 0.7, 0.15), c(u(x, y, 0.25) 1.7, v(x, y, 0.25) + 0.65, 0.15));
}

T ey(T x, T y)
{
　　return fmin(c(x + 0.4, y + 0.35, 0.1), c(x + 0.15, y + 0.35, 0.1));
}

T pu(T x, T y)
{
　　return fmin(c(x + 0.38, y + 0.33, 0.03), c(x + 0.13, y + 0.33, 0.03));
}

T fr(T x, T y)
{
　　return c(x * 1.1 - 0.3, y + 0.1, 0.15);
}

T mo(T x, T y)
{
　　return fmax(c(x + 0.15, y - 0.05, 0.2), -c(x + 0.15, y, 0.25));
}

T o(T x, T y, T(f)(T, T), T i)
{
　　T r =f(x, y);

　　return fabs(r) < 0.02 ? (atan2(f(x, y + 1e-3) - r, f(x + 1e-3, y) - r) + 0.3) 1.273 + 6.5 : r < 0 ? i : 0;
}

T s(T x, T y, T(*f)(T, T), T i)
{
　　return f(x, y) < 0 ? i : 0;
}

T f(T x, T y)
{
　　return o(x, y, no, 1) ? fmax(o(x, y, no, 1), s(x, y, nh, 12)) : fmax(o(x, y, fa, 1), fmax(o(x, y, ey, 11), fmax(o(x, y, ea, 1), fmax(o(x, y, mo, 1), fmax(s(x, y, fr, 13), s(x, y, pu, 12))))));
}

int main(int a, char **b)
{
　　for (T y = -1, s = a > 1 ? strtod(b[1], 0) : 1; y < 0.6; y += 0.05 / s, putchar('\n'))
　　{
　　　　for (T x = -1; x < 0.6; x += 0.025 / s)
　　　　{
　　　　　　putchar(" .|/=\|/=\| @!"[(int)f(u(x, y, 0.3), v(x, y, 0.3))]);
　　　　}　　
　　}
　　getchar();
　　return 0;
}

两倍：

四倍：

参考：

知乎Milo Yip