图的存储结构(邻接矩阵与邻接表)及其C++实现

一、图的定义

图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：

　　　　　　　　　　　　　　　　　　　G=(V，E)

其中：G表示一个图，V是图G中顶点的集合，E是图G中顶点之间边的集合。

注：

在线性表中，元素个数可以为零，称为空表；

在树中，结点个数可以为零，称为空树；

在图中，顶点个数不能为零，但可以没有边。

二、图的基本术语

略。

三、图的遍历

　　图的遍历是在从图中某一顶点出发，对图中所有顶点访问一次且仅访问一次。

　　图的遍历操作要解决的关键问题：

　　① 在图中，如何选取遍历的起始顶点？

　　解决方案：从编号小的顶点开始 。

　　在线性表中，数据元素在表中的编号就是元素在序列中的位置，因而其编号是唯一的； 在树中，将结点按层序编号，由于树具有层次性，因而其层序编号也是唯一的； 在图中，任何两个顶点之间都可能存在边，顶点是没有确定的先后次序的，所以，顶点的编号不唯一。 为了定义操作的方便，将图中的顶点按任意顺序排列起来，比如，按顶点的存储顺序。

　　② 从某个起点始可能到达不了所有其它顶点，怎么办？

　　解决方案：多次调用从某顶点出发遍历图的算法。

　　③ 因图中可能存在回路，某些顶点可能会被重复访问，那么如何避免遍历不会因回路而陷入死循环。

　　解决方案：附设访问标志数组visited[n] 。

　　④ 在图中，一个顶点可以和其它多个顶点相连，当这样的顶点访问过后，如何选取下一个要访问的顶点？

　　解决方案：深度优先遍历和广度优先遍历。

　　1、深度优先遍历

　　基本思想 ：

　　⑴ 访问顶点v；

　　⑵ 从v的未被访问的邻接点中选取一个顶点w，从w出发进行深度优先遍历；

　　⑶ 重复上述两步，直至图中所有和v有路径相通的顶点都被访问到。

　　2、广度优先遍历

　　基本思想：

　　⑴ 访问顶点v；

　　⑵ 依次访问v的各个未被访问的邻接点v1, v2, …, vk；

　　⑶ 分别从v1，v2，…，vk出发依次访问它们未被访问的邻接点，并使“先被访问顶点的邻接点”先于“后被访问顶点的邻接点”被访问。直至图中所有与顶点v有路径相通的顶点都被访问到。

四、图的存储结构

　　 是否可以采用顺序存储结构存储图?

　　图的特点：顶点之间的关系是m:n，即任何两个顶点之间都可能存在关系（边），无法通过存储位置表示这种任意的逻辑关系，所以，图无法采用顺序存储结构。

　　如何存储图?

　　考虑图的定义，图是由顶点和边组成的，分别考虑如何存储顶点、如何存储边。

　　①邻接矩阵（数组表示法）

　　基本思想：用一个一维数组存储图中顶点的信息，用一个二维数组（称为邻接矩阵）存储图中各顶点之间的邻接关系。

　　假设图G＝(V，E)有n个顶点，则邻接矩阵是一个n×n的方阵，定义为：

　　　　　　　　　　　　　　　　　　　　

　　

　　

　　

　　

　　

　　

　　

　　

　　

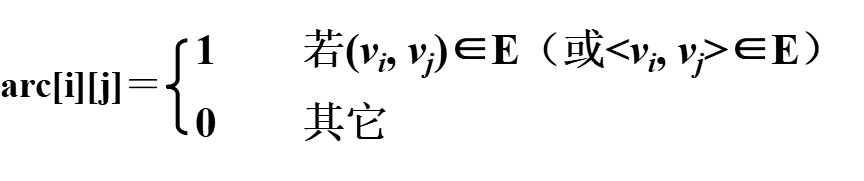
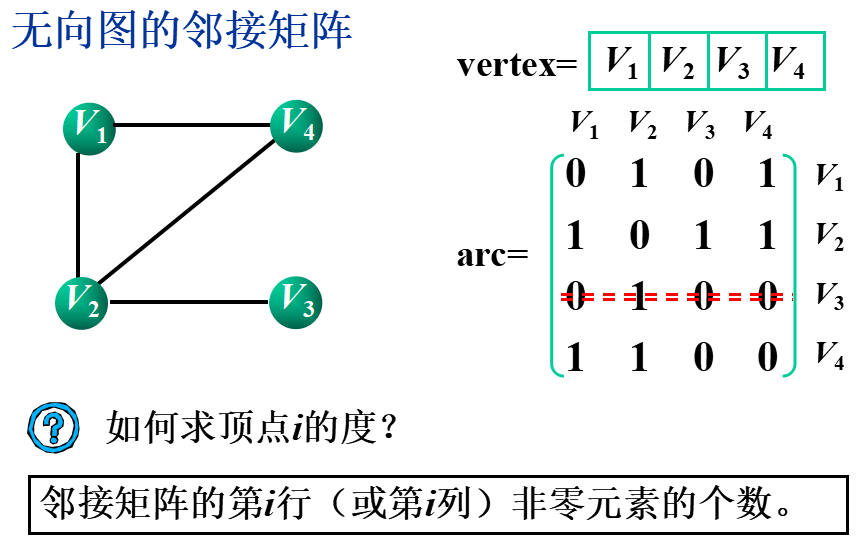
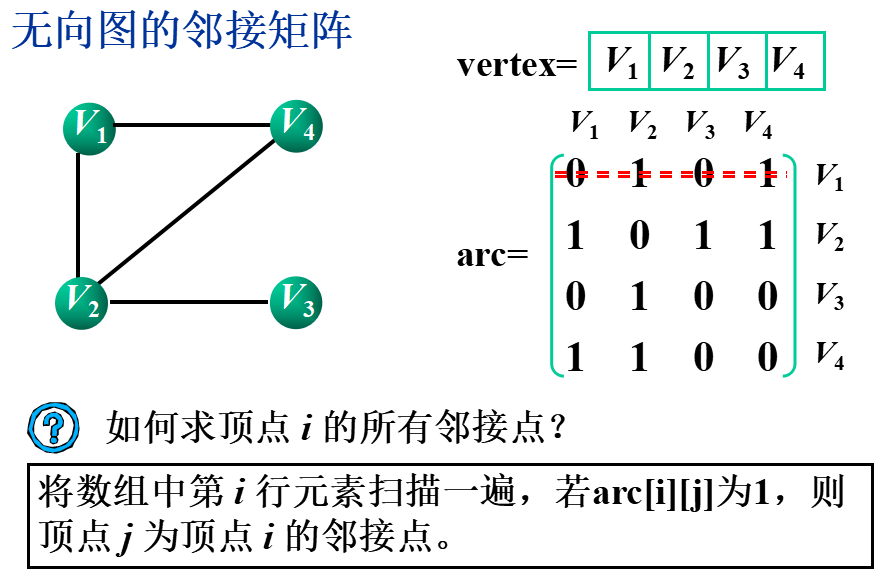
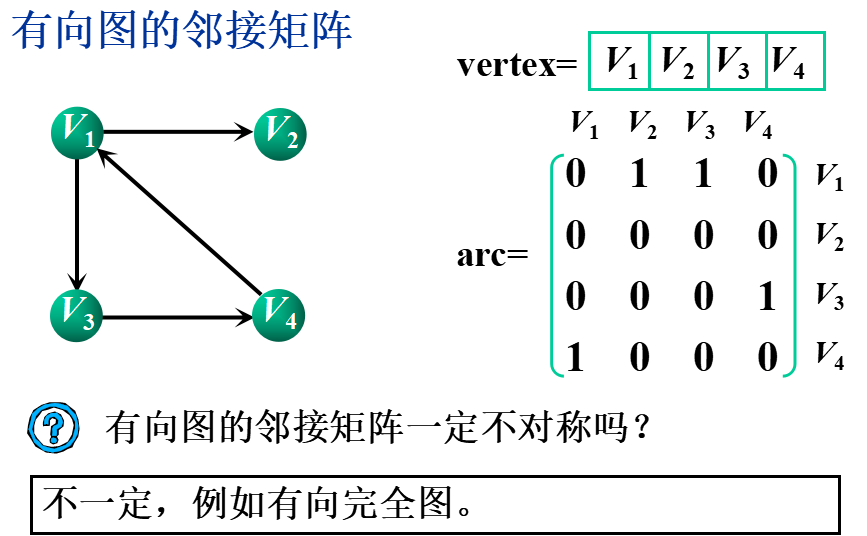
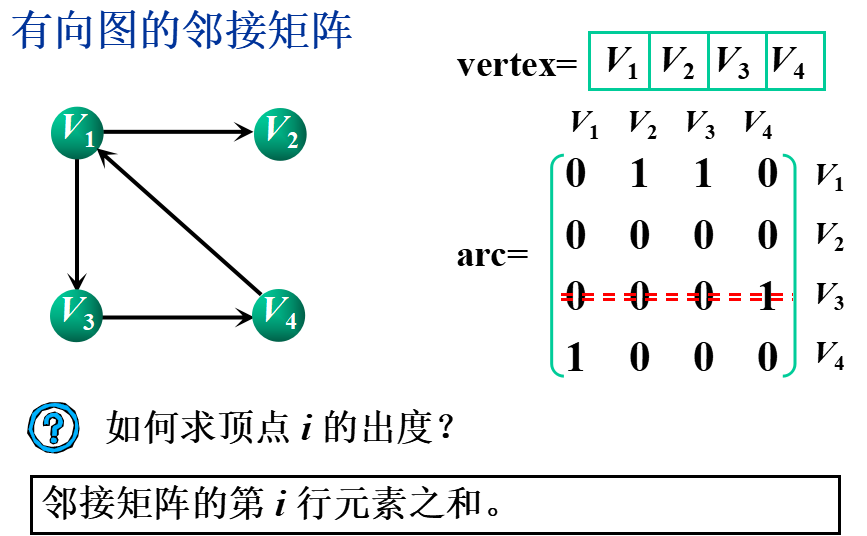
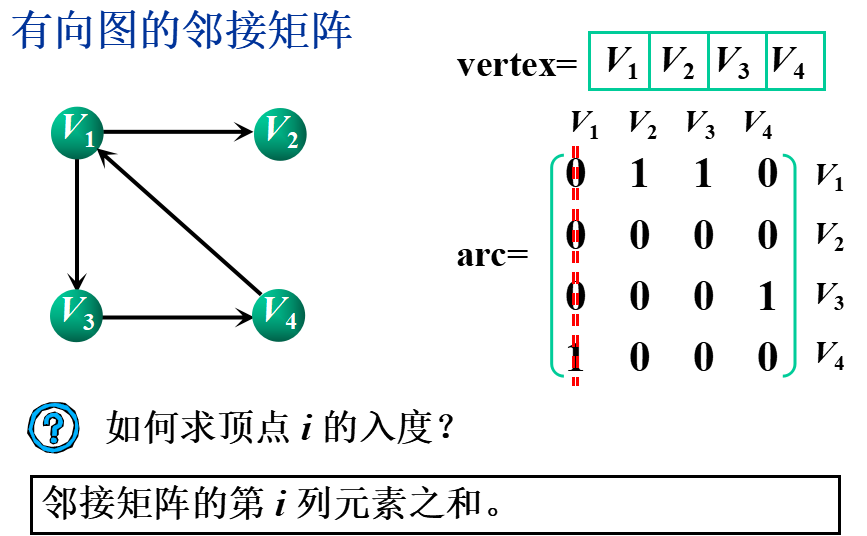
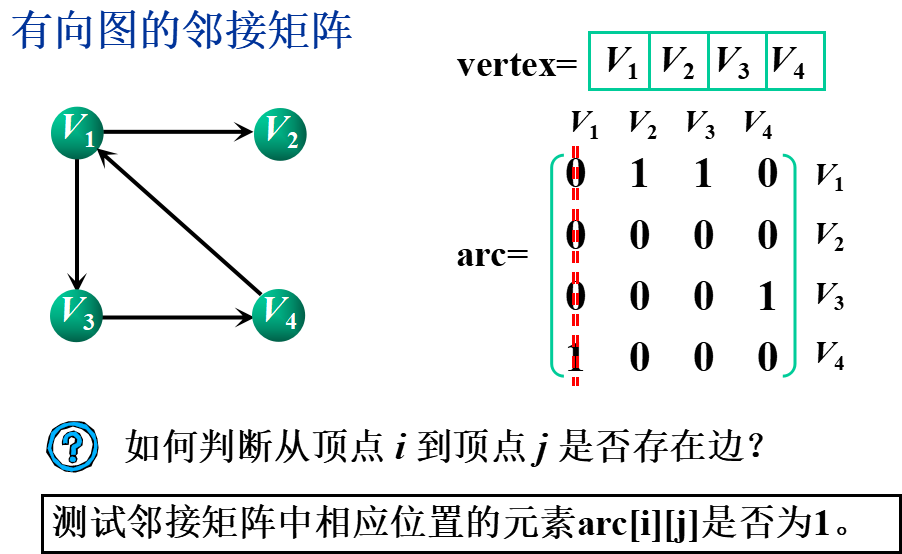
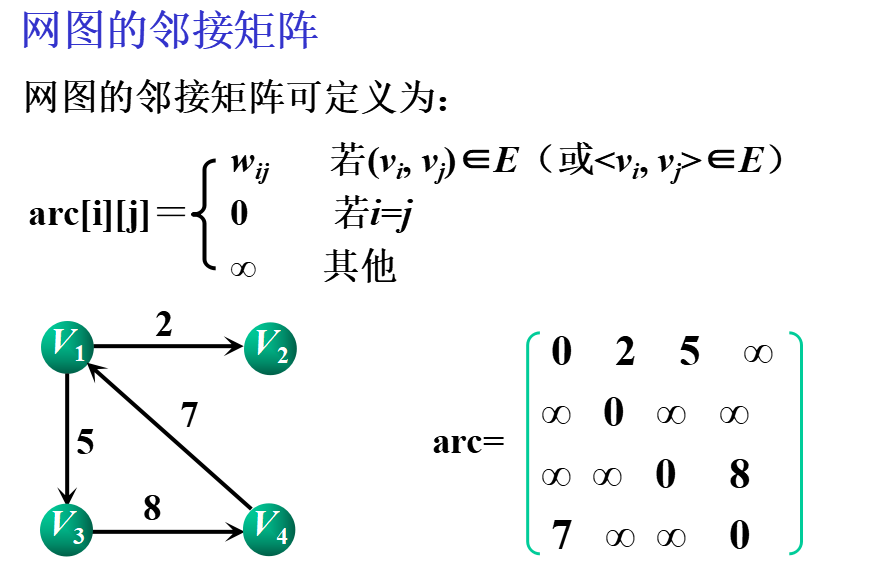
　　②邻接表

　　邻接表存储的基本思想：对于图的每个顶点vi，将所有邻接于vi的顶点链成一个单链表，称为顶点vi的边表（对于有向图则称为出边表），所有边表的头指针和存储顶点信息的一维数组构成了顶点表。

　　邻接表有两种结点结构：顶点表结点和边表结点.。

　　　　　　　　　　　　　　　　　　　　　　　　　　顶点表　　　　　　　　　　　　　　　　　　边表

　　其中：vertex：数据域，存放顶点信息。 firstedge：指针域，指向边表中第一个结点。 adjvex：邻接点域，边的终点在顶点表中的下标。 next：指针域，指向边表中的下一个结点。

　　定义邻接表的结点：

// 边表顶点
struct ArcNode
{    int adjvex;
      ArcNode *next;
};
// 顶点表
template <class T>
struct VertexNode
{
      T vertex;
      ArcNode *firstedge;
};

五、C++代码实现

Ⅰ、邻接矩阵

// queue.h
#pragma once
#include <iostream>
const int queueSize = ;
template<class T>
class queue
{
public:
    T data[queueSize];
    int front, rear;
};
// graph.h
#pragma once
#include<iostream>
#include"queue.h"
// 基于邻接矩阵存储结构的图的类实现
const int MaxSize = ;
int visited[MaxSize] = {  };// 顶点是否被访问的标记
template<class T>
class MGraph
{
public:
    MGraph(T a[], int n, int e);// 构造函数建立具有N个定点e条边的图
    ~MGraph(){}// 析构函数
    void DFSTraaverse(int v);// 深度优先遍历图
    void BFSTraverse(int v);// 广度优先遍历图
private:
    T vertex[MaxSize];// 存放图中顶点的数组
    int arc[MaxSize][MaxSize];// 存放图中边的数组
    int vertexNum, arcNum;// 图中顶点数和边数
};

template<class T>
inline MGraph<T>::MGraph(T a[], int n, int e)
{
    vertexNum = n;
    arcNum = e;
    for (int i = ; i < vertexNum; i++) // 顶点初始化
        vertex[i] = a[i];
    for (int i = ; i < vertexNum; i++) // 邻接矩阵初始化
        for (int j = ; j < vertexNum; j++)
            arc[i][j] = ;
    for (int k = ; k < arcNum; k++)
    {
        int i, j;
        std::cin >> i >> j;        // 输入边依附的顶点的编号
        arc[i][j] = ;            // 置有边标记
        arc[j][i] = ;
    }
}

template<class T>
inline void MGraph<T>::DFSTraaverse(int v)
{
    cout << vertex[v]<<" ";
    visited[v] = ;
    for (int j = ; j < vertexNum; j++)
    {
        if (arc[v][j] ==  && visited[j] == )
            DFSTraaverse(j);
    }
}

template<class T>
inline void MGraph<T>::BFSTraverse(int v)
{
    int visited[MaxSize] = {  };// 顶点是否被访问的标记
    queue<T> Q;
    Q.front = Q.rear = -;    // 初始化队列
    cout << vertex[v]<<" ";
    visited[v] = ;
    Q.data[++Q.rear] = v;    // 被访问顶点入队
    while (Q.front != Q.rear)
    {
        v = Q.data[++Q.front];    // 对头元素出队
        for (int j = ; j < vertexNum; j++)
        {
            if (arc[v][j] ==  && visited[j] == )
            {
                std::cout << vertex[j]<<" ";
                visited[j] = ;
                Q.data[++Q.rear] = j;    // 邻接点入队
            }
        }
    }
}
// main.cpp
#include"graph.h"
using namespace std;
int main()
{
    int arry[] = { ,,,,, };
    MGraph<int> graph(arry, , );
    graph.BFSTraverse();
    cout << endl;
    graph.DFSTraaverse();
    system("pause");
    return ;
}

Ⅱ、邻接表

// queue.h
#pragma once
#include <iostream>
const int queueSize = ;
template<class T>
class queue
{
public:
    T data[queueSize];
    int front, rear;
};
// graph.h
#pragma once
#include<iostream>
#include"queue.h"
// 定义边表结点
struct ArcNode
{
    int adjvex;// 邻接点域
    ArcNode* next;
};
// 定义顶点表结点
struct VertexNode
{
    int vertex;
    ArcNode* firstedge;
};

// 基于邻接表存储结构的图的类实现
const int MaxSize = ;
int visited[MaxSize] = {  };// 顶点是否被访问的标记
//typedef VertexNode AdjList[MaxSize];    //邻接表
template<class T>
class ALGraph
{
public:
    ALGraph(T a[], int n, int e);// 构造函数建立具有N个定点e条边的图
    ~ALGraph() {}// 析构函数
    void DFSTraaverse(int v);// 深度优先遍历图
    void BFSTraverse(int v);// 广度优先遍历图
private:
    VertexNode adjlist[MaxSize];// 存放顶点的数组
    int vertexNum, arcNum;// 图中顶点数和边数
};

template<class T>
ALGraph<T>::ALGraph(T a[], int n, int e)
{
    vertexNum = n;
    arcNum = e;
    for (int i = ; i <vertexNum; i++)
    {
        adjlist[i].vertex = a[i];
        adjlist[i].firstedge = NULL;
    }
    for (int k = ; k < arcNum; k++)
    {
        int i, j;
        std::cin >> i >> j;
        ArcNode* s = new ArcNode;
        s->adjvex = j;
        s->next = adjlist[i].firstedge;
        adjlist[i].firstedge = s;
    }
}

template<class T>
inline void ALGraph<T>::DFSTraaverse(int v)
{
    std::cout << adjlist[v].vertex;
    visited[v] = ;
    ArcNode* p = adjlist[v].firstedge;
    while (p != NULL)
    {
        int j = p->adjvex;
        if (visited[j] == )
            DFSTraaverse(j);
        p = p->next;
    }
}

template<class T>
inline void ALGraph<T>::BFSTraverse(int v)
{
    int visited[MaxSize] = {  };// 顶点是否被访问的标记
    queue<T> Q;
    Q.front = Q.rear = -;    // 初始化队列
    std::cout << adjlist[v].vertex;
    visited[v] = ;
    Q.data[++Q.rear] = v;// 被访问顶点入队
    while (Q.front != Q.rear)
    {
        v = Q.data[++Q.front];    // 对头元素出队
        ArcNode* p = adjlist[v].firstedge;
        while (p != NULL)
        {
            int j = p->adjvex;
            if (visited[j] == )
            {
                std::cout << adjlist[j].vertex;
                visited[j] = ;
                Q.data[++Q.rear] = j;
            }
            p = p->next;
        }
    }
}
// main.cpp
#include"graph.h"
using namespace std;
int main()
{
    int arry[] = { ,,,, };
    ALGraph<int> graph(arry, , );
    graph.BFSTraverse();
    cout << endl;
    graph.DFSTraaverse();
    system("pause");
    return ;
}

参考文献：

[1]王红梅, 胡明, 王涛. 数据结构(C++版)[M]. 北京：清华大学出版社。

2018-01-07