HDU 1978 How many ways DP问题

How many ways

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2568    Accepted Submission(s): 1509

Problem Description

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。

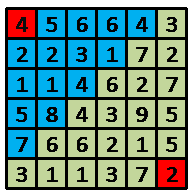
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)

点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

Input

第一行输入一个整数T,表示数据的组数。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

 

Output

对于每一组数据输出方式总数对10000取模的结果.

 

Sample Input

1

6 6

4 5 6 6 4 3

2 2 3 1 7 2

1 1 4 6 2 7

5 8 4 3 9 5

7 6 6 2 1 5

3 1 1 3 7 2

Sample Output

3948

讲解这样的题目 还是比较有意思的，看着像是搜索题目，但是吧，用常规搜索吧，容易超时，于是乎，动态规划解决，还是挺简单的；

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<map>
 #include<queue>
 using namespace std;
 int a[][];
 long long dp[][];
 const int mod=;
 int main()
 {
     int k,t,m,n,k1,k2;
     cin>>t;
     while(t--)
     {
         k1=;k2=;
         memset(dp,,sizeof(dp));
         dp[][]=;
         cin>>m>>n;
         for(int i=;i<=m;i++)
             for(int j=; j<=n; j++)
                scanf("%d",&a[i][j]);
         for(int i=; i<=m; i++ )
             for(int j= ;j<=n; j++)
             {
             k1=min(i+a[i][j],m);     //在找到的点的右，下，开始dp；
             for(int k=i ; k<=k1; k++)
                {
                    k2=min(j+a[i][j]-k+i,n);
                     for(int l=j; l<=k2; l++)
                     {
                         if(k!=i || l!=j)
                             dp[k][l]=dp[k][l]+dp[i][j];
                             if(dp[k][l]>=mod) dp[k][l]%=mod;
                     }
                }
             }
         cout<<dp[m][n]%mod<<endl;
     }
     return ;
 }