Deep Linear Networks with Arbitrary Loss: All Local Minima Are Global

目录

• 问题
• 假设和重要结果
• 证明
• 注

Laurent T, Von Brecht J H. Deep linear networks with arbitrary loss: All local minima are global[C]. international conference on machine learning, 2018: 2902-2907.

问题

这篇文章是关于深度学习的一些理论分析.

假设这么一个网络:

\[\hat{y}^{(i)}=W_LW_{L-1}\cdots W_1 x^{(i)}.
\]

其中\(x\)是输入，\(W_k\)是第\(k\)层的权重，而\(\hat{y}\)是最后的输出. 没错，这篇文章研究的是深度线性网络的性质(没有激活函数). 当然，这样子，无论有多少层，这个网络最后是一个普通线性函数，所以，作者的本意应该只是借此来窥探深度学习的一些性质.

作者证明了，在满足一定条件下，这个深度线性网络，任何局部最优解都是全局最优解.

假设和重要结果

损失函数如此表示:

\[\mathcal{L}(W_1, \ldots, W_L)=\frac{1}{N} \sum_{i=1}^N \ell (\hat{y}^{(i)}, y^{(i})
\]

假设

1. \(d_k\)表示第\(k+1\)层的神经元个数，即\(d_0\)表示输入层的维度，\(W_k \in \mathbb{R}^{d_{k-1} \times d_k}\), \(d_L\)表示输出层的维度,
2. \(d_k \ge \min \{d_0, d_L\}, 0 < k < L\),
3. 损失函数关于\(\hat{y}\)凸且可微.

定理1：满足上面假设的深度线性网络，任意局部最优都是全局最优.

考虑下面问题p(2):

\[\min \quad f(W_LW_{L-1}\cdots W_1),
\]

并记\(A=W_LW_{L-1}\cdots W_1\).

则:

定理3:

假设\(f(A)\)是任意的可微函数，且满足:

\[\min \{d_1, \ldots, d_{L-1}\} \ge \min \{d_0, d_L\},
\]

则关于p(2)的任意的极小值点\((\hat{W}_1, \ldots, \hat{W}_L)\)，都将满足:

\[\nabla f(\hat{A})=0 \quad \hat{A} := \hat{W}_L \hat{W}_{L-1}\cdots \hat{W}_1.
\]

证明

注意到, 可表示成:

\[\mathcal{L} (W_1, \ldots, W_L)=f(W_L\cdots W_1).
\]

则\(f(A)\)是关于\(A\)的凸的可微函数(注意是关于\(A\)), 所以，当\(\nabla f(\hat{A})=0\)的时候，\(\hat{A}\)便是\(f\)，即\(\mathcal{L}\)得最小值点. 这意味着，只要我们证明了定理3，也就证明了定理1.

下证定理3:

首先定义:

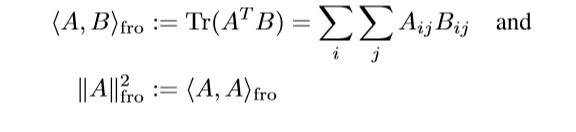
记:

\[F(W_1, \ldots, W_L) := f(W_L \cdots W_1).
\]

容易证明(这部分论文中也给出了证明，不在此贴出):



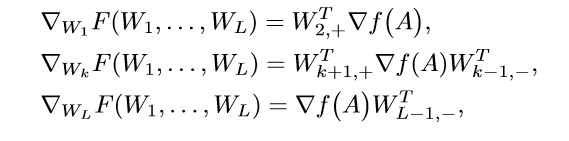
其中:



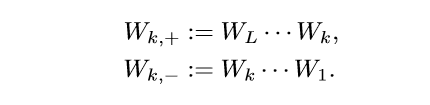
不失一般性，假设\(d_L\ge d_0\), 因为令:

\[g(A) := f(A^T)
\]

则，\(g\)定义在\(d_0 \times d_L\)之上，且\(A^T\)使得\(f\)为极小值，当且仅当\(A\)使得\(g\)为极小值，所以\(d_0, d_L\)的地位是相同的，我们可以直接假设\(d_L \ge d_0\).

\((\hat{W}_1, \ldots, \hat{W}_L)\)是最小值点，则存在\(\epsilon>0\)， 使得满足:



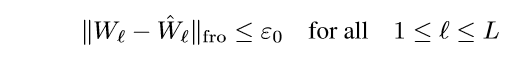
的点满足:

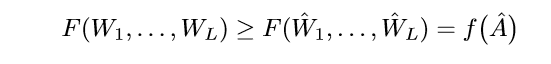
于是:



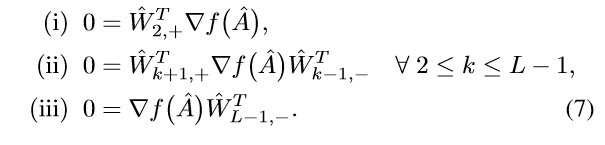
当\(\mathrm{ker}(\hat{W}_{L-1}) = \{0\}\)的时候:

\[\nabla f(\hat{A})=0.
\]

于是只要证明, \(\ker(\hat{W}_{L-1}) = \not \{0\}\)的时候，上式也成立即可.

我们的想法是构造一族极小值点, 满足:

\[\widetilde{A}=A,
\]

通过一些性质，推出\(\nabla f(\hat{A})=0\).

首先证明，满足:



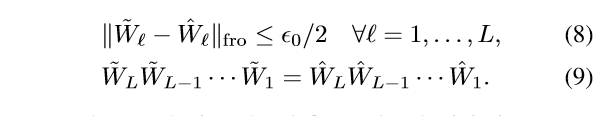
的点都是极小值点.

因为:

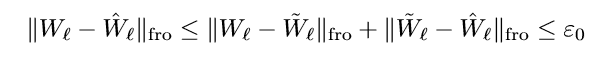
所以:



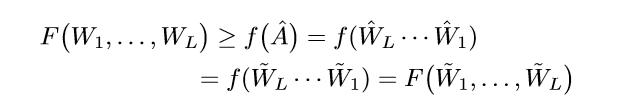
所以\((\tilde{W}_1, \ldots, \tilde{W}_L)\)也是一个极小值点.

那么如何来构造呢?

可知:



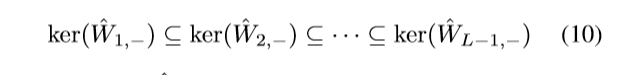
对\(\hat{W}_{k, -}\)进行奇异值分解:



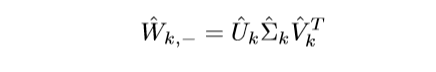
因为\(d_k \ge d_0, k\ge1\), 所以其分解是这样的:



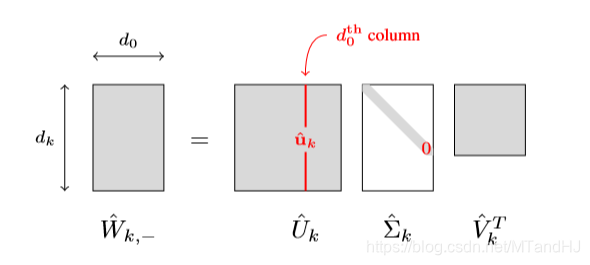
注意到，这里体现了为什么需要\(d_k\ge \min \{d_L, d_0\}\)， 否则\(\mathrm{ker}(\hat{W}_{k, -})\)不可能等于\(\{0\}\)(因为其秩永远小于\(d_0\)).

假设\(k_*\)是第一个\(\mathrm{ker}(\hat{W}_{k, -}) = \not\{0\}\)的，则下面的构造便是我们所需要的:



其中\(\hat{u}_{k-1}\)表示\(\hat{W}_{k-1, -}\)奇异值分解\(\hat{U}_{k-1}\)的\(d_0\)列, 很明显，满足\(\hat{u}_{k-1}^T\hat{W}_{k-1,-}=0, k\ge k^* + 1\).

条件(8)容易证明，用数学归纳法证明(9):

第一项成立，假设第\(k\)项也成立, 于是



也成立，所以条件成立.

既然满足其构造方式的所有点都是点都是极小值点，那么:



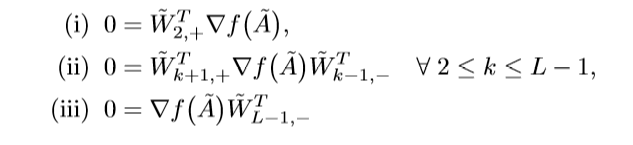
注意，对所有的满足条件的\(\delta_k, w_k\)都成立.

\(k_* > 1\)的时候可得:



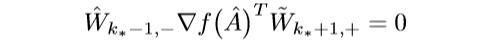
又\(\mathrm{ker}(\hat{W}_{k_*-1,-})=\{0\}\), 所以:



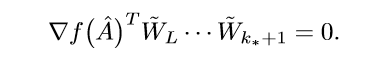
注意到\(k_*=1\)的时候，也有上面的形式.

首先，令\(\delta_{k_*+1}=0\), 则\(\tilde{W}_{k_*+1}=\hat{W}_{k_*+1}\), 于是:

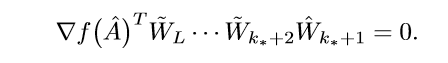
在去任意\(\delta_{k_*+1} > 0\)， 与上式作差可得:



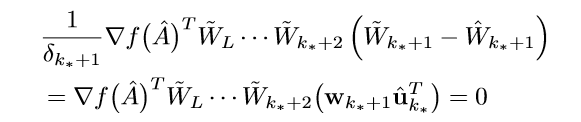
俩边同乘上\(\hat{u}_{k_*}^T\)可得:



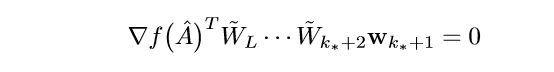
因为\(w_{k_*+1}\)是任意的，所以，左端为0，以此类推，最后可得:

\[\nabla f(\tilde{A})=\nabla f(\hat{A})=0.
\]

证毕.

注

我没有把定理2放上来.

有一个方向，定理3中的极小值点改成极大值点，似乎定理也成立，即：

假设\(f(A)\)是任意的可微函数，且满足:

\[\min \{d_1, \ldots, d_{L-1}\} \ge \min \{d_0, d_L\},
\]

则关于p(2)的任意的极大值点\((\hat{W}_1, \ldots, \hat{W}_L)\)，都将满足:

\[\nabla f(\hat{A})=0 \quad \hat{A} := \hat{W}_L \hat{W}_{L-1}\cdots \hat{W}_1.
\]

我自己仿照论文的证明是可以证明出来的，不过，既然\(\nabla f(\hat{A})=0\), 那么\(\hat{A}\)依然是\(\mathcal{L}\)的最小值点，是不是可以这么认为，\(f\)压根没有存粹的极大值点.

另外作者指出，极小值点不能改为驻点，因为\(A=0\)便是一个驻点，但是没有\(f(0)\)必须为0的规定.

此外作者还说明了，为什么要可微等等原因，详情回见论文.