CF1225E题解 Rock Is Push

在打CF的时候没想到www这个dp真的蛮巧妙的

这是一道dp题（废话

假设我们走到了\((i,j)\)位置，因为我们只能下移/右移，那么我们所有上方与左方的石块（即\(\{ (i,j)|i<n \space || \space j<m \}\)的石块）不管被推到那里都与我无瓜（可以画几张图略推一推，还是比较明显），即该题无后效性，可用dp求解。

合在一起不是很好算，我们可以考虑将右移与下移分开对其进行dp。

因此我们可以用数组\(rs,ds\)来记录某位置右边的石头数量以及下方的石头数量，因为只有这些石头对\((i,j)\)的状态转移有关

设二维状态数组\(r,d\)，表示在\((i,j)\)位置时下一步向右（\(r\)）或向下（\(d\)）走，到达目标位置\((n,m)\)的方案总数，由定义可得\(r[n][m]=d[n][m]=1\)。

重点来惹w：状态转移方程

之所以说这道题巧妙，一是因为它分成了\(r,d\)两块来dp，再一个就是状态转移方程了。

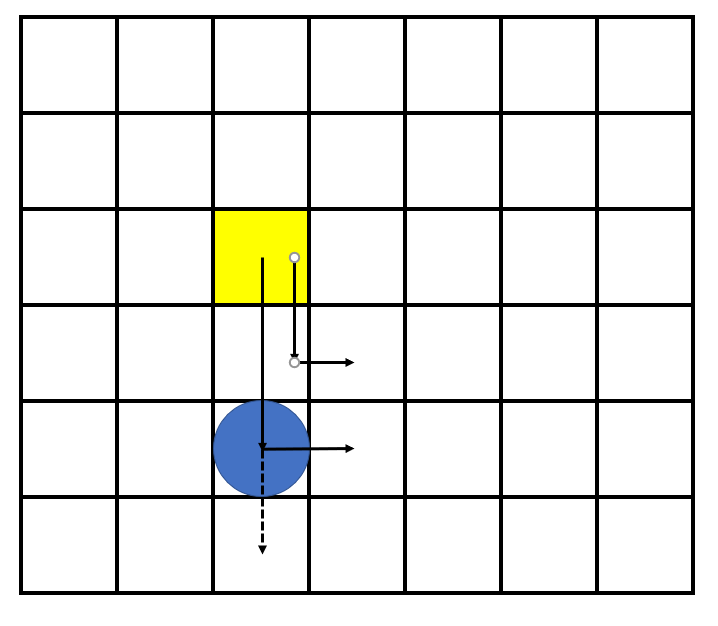
如上图所示，假设我们在黄色格子\((i,j)\)，蓝色圆形为石头，虚线为石头移动轨迹。那么易得\(ds[i][j]=1\)（\(rs\)定义忘了的看上文）。因为我们下一步必须向下走，所以我们可以选择连续走\(1\)步、\(2\)步、...一直到\(n-i-ds[i][j]\)步为止，此时下面的石头刚好全部被一个接一个地推到了墙上排好。因此状态转移方程即

\[d[i][j]=\sum_{k=1}^{n-i-ds[i][j]}r[i][j+k]
\]

\[r[i][j]=\sum_{k=1}^{m-i-rs[i][j]}d[i+k][j]
\]

（提前解一个疑：这里对\(r\)数组进行求和而非\(d\)数组求和的原因是我们连续往下走了\(k\)步后下一步应该往右，因此这里用\(r\)，反之亦然）

想想还是蛮巧的（或者是窝太弱啦qaq

当然一个一个枚举\(r[i][j+k],d[i+k][j]\)肯定会超时，因此这里我们使用前缀和保存。

注意：代码里的 \(ds,rs\) 及 \(sumd,sumr\) 意义都搞反了（ 感谢：@11eyes

code：

#include<bits/stdc++.h>
using namespace std;
long long n , m , r[2100][2100] , d[2100][2100] , ds[2100][2100] , rs[2100][2100];
long long sumr[2100][2100] , sumd[2100][2100];
const int mod = 1e9 + 7;
char s[2100];
//d:down r:right (update：反了
int main()
{
	scanf("%d%d" , &n , &m);
	for(register int i = 1 ; i <= n ; i++ )
	{
		scanf("%s" , s + 1);
		for(register int j = 1 ; j <= m ; j++ )
		{
			if(s[j] == 'R') rs[i][j] = 1 , ds[i][j] = 1;
		}
	}
	if(n == 1 && m == 1)
	{
		cout << (rs[1][1] ^ 1);
		return 0;
	}
	for(register int i = n ; i >= 1 ; i-- )
	{
		for(register int j = m ; j >= 1 ; j-- )
		{
			ds[i][j] += ds[i][j + 1];
			rs[i][j] += rs[i + 1][j];
		}
	}
	r[n][m] = d[n][m] = sumd[n][m] = sumr[n][m] = 1;
	for(register int i = n ; i >= 1 ; i-- )
	{
		for(register int j = m ; j >= 1 ; j-- )
		{
			if(i == n && j == m) continue;
			r[i][j] = (sumd[i][j + 1] - sumd[i][m - ds[i][j + 1] + 1]) % mod;
			d[i][j] = (sumr[i + 1][j] - sumr[n - rs[i + 1][j] + 1][j]) % mod;
			sumr[i][j] = (sumr[i + 1][j] + r[i][j]) % mod;
			sumd[i][j] = (sumd[i][j + 1] + d[i][j]) % mod;
		}
	}
	/*for(register int i = 1 ; i <= n ; i++ )
	{
		for(register int j = 1 ; j <= m ; j++ )
		{
			cout << d[i][j] << ' ';
		}
		cout << endl;
	}
	cout << endl;
	for(register int i = 1 ; i <= n ; i++ )
	{
		for(register int j = 1 ; j <= m ; j++ )
		{
			cout << r[i][j] << ' ';
		}
		cout << endl;
	}*/
//	cerr << r[1][1] << " " << d[1][1] << endl;
	cout << ((r[1][1] + d[1][1]) % mod + mod) % mod;
	return 0;
}