OpenCV 之 空间刚体变换

刚体就是 "刚性物体"，它在运动过程中，内部各质点间的相对位置不会改变，也即 每两个质点间的距离 保持不变

假设刚体内任意两个质点，坐标分别为 $(x_1, y_1, z_1)$ 和 $(x_2, y_2, z_2)$，则在刚体运动过程中，这两个质点满足如下条件：

$\quad \left( (x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2 \right) |_t = l^2$

例如：影视剧《西游记》中的法宝金刚琢、玉净瓶是刚体；而幌金绳、芭蕉扇等，则不是刚体

1  刚体变换

1.1  矩阵形式

OpenCV 之 图像几何变换 中的等距变换，实际是二维刚体变换

$\quad \begin{bmatrix} x^{\prime} \\ y^{\prime} \\ 1 \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta & t_x \\ \sin \theta & \cos \theta & t_y \\ 0&0&1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1\end{bmatrix}$

从平面推及空间，三维刚体变换的矩阵形式为

$\quad \begin{bmatrix}x' \\ y' \\ z' \\ 1 \end{bmatrix}=\begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} &t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\z \\ 1\end{bmatrix} $

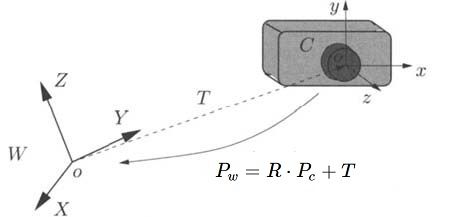
例如：空间任一点，在相机坐标系中为 $P_{c}(x, y, z)$，世界坐标系中为 $P_{w}(X, Y, Z)$ ，则 $P_c$ -> $P_w$ 就是一个刚体变换

1.2  约束分析

R 和 T 共有 12 个未知数，但 R 是标准正交矩阵，自带 6 个约束方程，则刚体变换有 12 - 6 = 6 个自由度 (和直观的感受一致)

表面上看，似乎只需两组空间对应点，联立 6 个方程，便可求得 6 个未知数，但这 6 个方程是有冗余的 (因为这两组对应点，在各自的坐标系下，两点之间的距离是相等的)

因此，第二组对应点，只是提供了 2 个约束方程，加上第一组对应点的 3 个约束，共有 5 个独立的方程

显然，还需要第三组对应点，提供 1 个独立的方程，才能求出 R 和 T

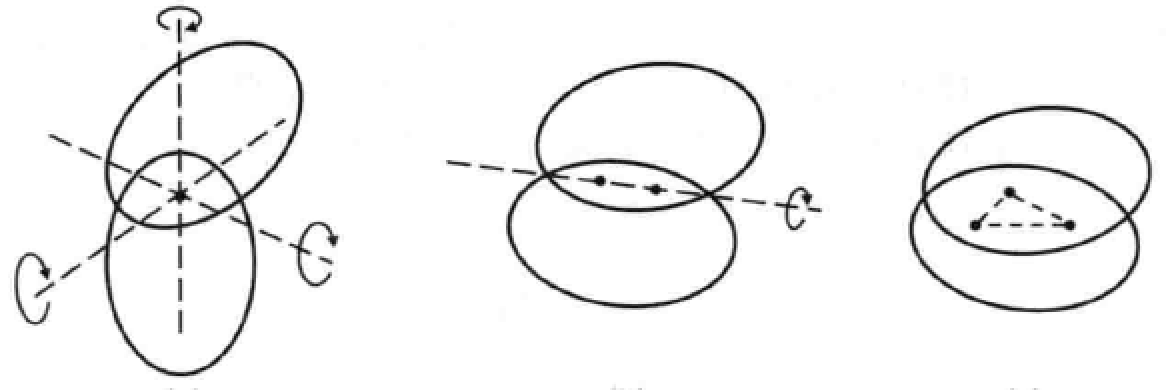
如图所示，两个刚体之间：1个点重合 => 3个自由度；2个点重合 => 1个自由度；3个点重合=> 0个自由度

1.3  直观理解

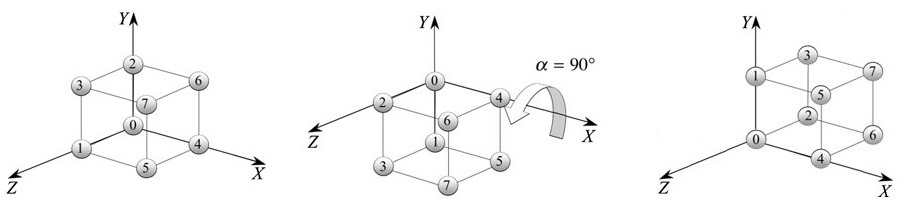
一个单位立方体，可在 X-Y-Z 坐标系中自由运动，则二者之间的转换关系，可视为刚体变换

单点重合：当立方体的角点 0 和 X-Y-Z 坐标系的原点 O 重合时，立方体还能自由的旋转 (X 轴 -> Y 轴 -> Z 轴)

两点重合：除了立方体的角点 0 和坐标系的 原点 O 重合外，再令角点 4 和 X 轴上的某点重合，则此时立方体只能 绕 X 轴旋转

三点重合：除了以上两个角点 0 和 4，如果再使角点 1 和 Z 轴上的某点重合，则立方体就会和 X-Y-Z 坐标系 牢牢的连接在一起

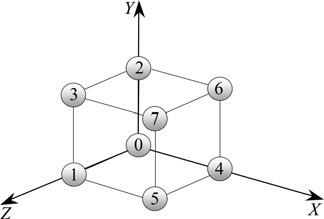
因此，选取不共面的三组对应点，联立方程组，便可求得 R 和 T

2  旋转向量

任意的旋转，都可用一个旋转轴 (axis) 和 绕轴旋转角 (angle) 来描述，简称“轴角”

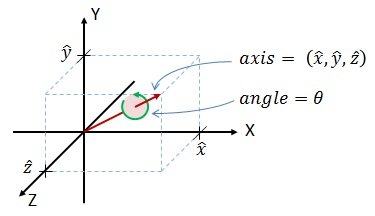
因此，可用一个方向和旋转轴一致，长度等于旋转角的向量来表示旋转，这个向量称为旋转向量 (或“旋量”)

假定旋转轴  $\mathbf{n} = [r_{x}, r_{y}, r_{z}]$，旋转角为  $\theta$，则旋转向量可记为 $\theta \mathbf{n}$

旋转向量到旋转矩阵的转换，可由罗德里格斯公式来实现，如下：

$\quad R = cos(\theta) I + (1 - cos \theta) \mathbf{nn^T} + sin \theta \begin{bmatrix} 0&-r_z&r_y \\ r_z&0&-r_x \\ -r_y&r_x&0 \end{bmatrix}$

反之，从旋转矩阵到旋量，公式如下：

$\quad \sin \theta \begin{bmatrix}0 &-r_z&r_y \\r_z&0&-r_x \\-r_y & r_x &0 \end{bmatrix} = \dfrac{R - R^T}{2} $

OpenCV 中有一个 Rodrigues() 函数，可实现二者的相互转换

void  Rodrigues (
      InputArray   src,  // 输入旋转向量 n(3x1 或 1x3) 或 旋转矩阵 R(3x3)
      OutputArray  dst,  // 输出旋转矩阵 R 或 旋转向量 n
      OutputArray  jacobian = noArray()  // 可选，输出 Jacobian 矩阵(3x9 或 9x3)
)       

3  欧拉角

3.1  定义

假定 X-Y 平面内有一点 P， 旋转 $\theta$ 角到 $P^{\prime}$ 位置，如下图：

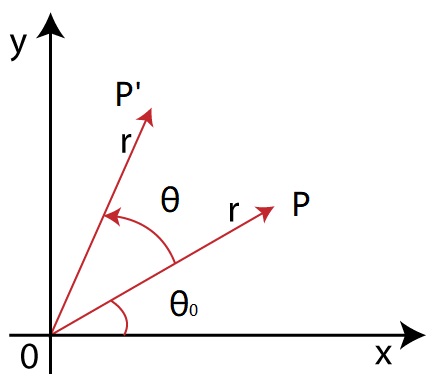
取 $\angle$POX = $\theta_0$，列方程组得

$\quad x^{\prime} = r \cos (\theta_0 + \theta) = r \cos \theta_0 \cos\theta - r \sin \theta_0 \sin\theta = x \cos\theta - y \sin \theta $

$\quad y^{\prime} = r \sin(\theta_0+ \theta) = r \sin\theta_0 cos \theta + r \cos \theta_0 \sin\theta = x \sin \theta + y \cos \theta $

转化为矩阵形式  $ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

3.2  欧拉角

将二维旋转矩阵 $R_{2 \times 2}$ 扩展到三维空间

1）绕 Z 轴旋转 roll，则添加 z 坐标 $\pmb{R_z} = \begin{bmatrix} cos \theta_z & -sin \theta_z & 0 \\ sin \theta_z & cos \theta_z & 0 \\ 0&0&1 \end{bmatrix}$

2）绕 Y 轴旋转 yaw，则添加 y 坐标  $\pmb{R_y} = \begin{bmatrix} cos \theta_y & 0 & \color{blue}{sin \theta_y} \\ 0 & 1 & 0 \\ \color{blue}{-sin \theta_y} & 0 & cos \theta_y \end{bmatrix}$

3）绕 X 轴旋转 pitch，则添加 x 坐标  $\pmb{R_x} = \begin{bmatrix} 1 & 0 & 0 \\ 0 &cos \theta_x & -sin \theta_x \\ 0 & sin \theta_x & cos \theta_x \end{bmatrix}$

因此，当按 Z-Y-X 的顺序旋转时，一个旋转矩阵就被分解成了绕不同轴的三次旋转，旋转角称为 "欧拉角"

$\quad R = R_z \cdot R_y \cdot R_x = \begin{bmatrix} cos \theta_y cos \theta_z & sin \theta_x sin \theta_y cos \theta_z - cos \theta_x sin \theta_z & sin \theta_x sin \theta_z + cos \theta_x sin \theta_y cos \theta_z \\ cos \theta_y sin \theta_z & cos \theta_x cos \theta_z + sin \theta_x sin \theta_y sin \theta_z & cos \theta_x sin \theta_y sin \theta_z - sin \theta_x cos \theta_z \\ -sin \theta_y & sin \theta_x cos \theta_y & cos \theta_x cos \theta_y \end{bmatrix} $，

注意：在使用欧拉角时，要先指明旋转的顺序，因为绕不同的轴旋转时得到的欧拉角也不同

反之，由旋转矩阵求解欧拉角，则有：

$\quad \theta_x = tan^{-1} (\dfrac{r_{32}}{r_{33}})$

$\quad \theta_y = sin^{-1} (-r_{33})$

$\quad \theta_z = tan^{-1} (\dfrac{r_{21}}{r_{11}})$

3.3  代码实现

已知绕三个轴旋转的欧拉角，要转换为旋转矩阵，直接套用公式

Mat eulerAnglesToRotationMatrix(Vec3f &theta)
{
    // Calculate rotation about x axis
    Mat R_x = (Mat_<double>(3,3) <<
               1,       0,              0,
               0,       cos(theta[0]),   -sin(theta[0]),
               0,       sin(theta[0]),   cos(theta[0])  );

    // Calculate rotation about y axis
    Mat R_y = (Mat_<double>(3,3) <<
               cos(theta[1]),    0,      sin(theta[1]),
               0,                1,      0,
               -sin(theta[1]),   0,      cos(theta[1])  );

    // Calculate rotation about z axis
    Mat R_z = (Mat_<double>(3,3) <<
               cos(theta[2]),    -sin(theta[2]),      0,
               sin(theta[2]),    cos(theta[2]),       0,
               0,                0,                   1  );

    // Combined rotation matrix
    Mat R = R_z * R_y * R_x;

    return R;
}

旋转矩阵到欧拉角的转换，要指明旋转顺序 (Z-Y-X 或 X-Y-Z 等 6 种)，下面代码实现了和 MATLAB 中 rotm2euler 一样的功能，只是旋转顺序不同 (X-Y-Z)

// Checks if a matrix is a valid rotation matrix.
bool isRotationMatrix(Mat &R)
{
    Mat Rt;
    transpose(R, Rt);
    Mat shouldBeIdentity = Rt * R;
    Mat I = Mat::eye(3,3, shouldBeIdentity.type());

    return  norm(I, shouldBeIdentity) < 1e-6;
}

// The result is the same as MATLAB except the order of the euler angles ( x and z are swapped ).
Vec3f rotationMatrixToEulerAngles(Mat &R)
{
    assert(isRotationMatrix(R));
    float sy = sqrt(R.at<double>(0,0) * R.at<double>(0,0) +  R.at<double>(1,0) * R.at<double>(1,0) );
    bool singular = sy < 1e-6; // If

    float x, y, z;
    if (!singular) {
        x = atan2(R.at<double>(2,1) , R.at<double>(2,2));
        y = atan2(-R.at<double>(2,0), sy);
        z = atan2(R.at<double>(1,0), R.at<double>(0,0));
    } else {
        x = atan2(-R.at<double>(1,2), R.at<double>(1,1));
        y = atan2(-R.at<double>(2,0), sy);
        z = 0;
    }
    return Vec3f(x, y, z);
}  

4  四元数

4.1  定义

四元数本质是一种高阶的复数，普通复数有一个实部和一个虚部，而四元数有一个实部和三个虚部

$\quad q = s + x \mathbf{i} + y \mathbf{j} + z \mathbf{k}$，其中 $\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=\mathbf{ijk}=-1$

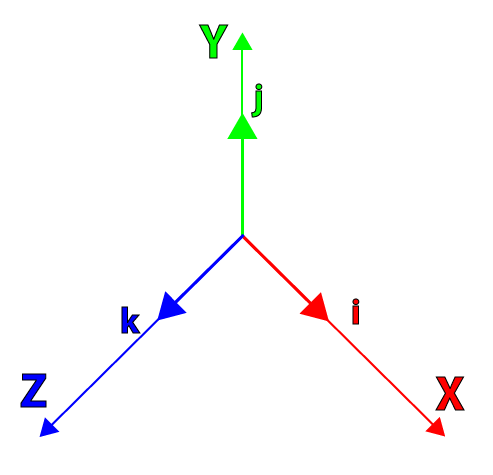
平面中任一点的旋转，可通过“左乘” 旋转向量来表示，如下：

$\quad p = a + b \mathbf{i} $，$q = cos \theta + \mathbf{i} sin \theta$

$\quad p^{\prime} = qp = a\cos\theta-b\sin\theta+(a\sin\theta+b\cos\theta)i $

推及空间中任一点的旋转，可通过“左乘”四元数来表示，如下：

$\quad p = [0, a \mathbf{i} + b \mathbf{j} + c \mathbf{k}]$，$q = [cos \theta, sin \theta \mathbf{v}  ]$，其中 $\mathbf{v}$ 由 $\mathbf{i}, \mathbf{j}, \mathbf{k}$ 组合而成

$\quad p^{\prime} = qp$

4.2  实例

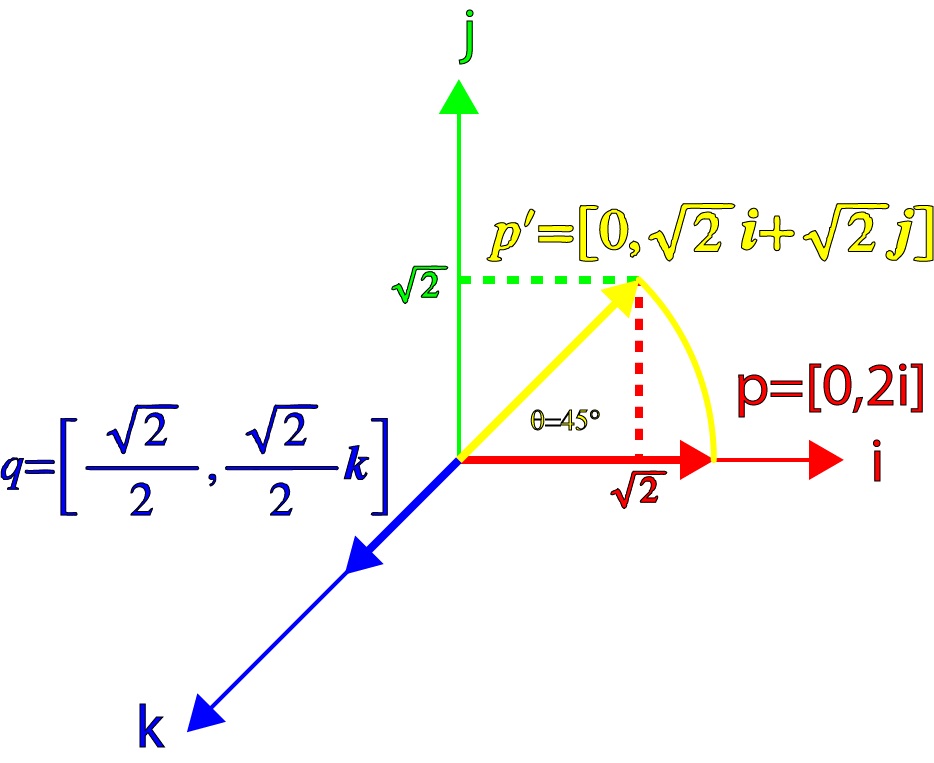
    例1：当向量 p 围绕 k 轴在 i-j 平面内旋转 45°，表示该旋转的四元数为

$\quad q = \left[\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2} \mathbf{k} \right] $

取 $p = [0, 2 \mathbf{i}]$，则 $p^{\prime} = qp = [0, \sqrt{2}\mathbf{i} + \sqrt{2} \mathbf{j}] $，如下图 p' 确实是 p 围绕 $\mathbf{k}$ 轴旋转 45° 得到的

    例2：当向量 p 围绕 q 旋转 45°，且 q 中的向量 v 在 i-k 平面内和 p 成 45° 时，表示该旋转的四元数为

$\quad q = \left[ \dfrac{\sqrt{2}}{2},  \dfrac{\sqrt{2}}{2} \left(\dfrac{\sqrt{2}}{2} \mathbf{i} + \dfrac{\sqrt{2}}{2} \mathbf{k} \right) \right]$

取 $p = [0, 2 \mathbf{i}]$，则 $p^{\prime} = qp = [-1,\sqrt{2}\mathbf{i}+\mathbf{j}]$，可看出 $p^{\prime}$ 中向量模长为 $\sqrt{3}$，这不再是一个纯旋转的变换

但如果再“右乘” $q^{-1}$，则 $p^{\prime} = qpq^{-1} = [0,\mathbf{i}+\sqrt{2}\mathbf{j}+\mathbf{k} ]$

如下图，这又变成了一个纯旋转，但是旋转的角度是 90°，不是 45°

综上所述，向量 p 围绕任一轴 $\mathbf{v}$ 旋转 $\theta$，则表示该旋转的四元数形式为

$\quad q=\left[\cos\dfrac{\theta}{2},\sin\dfrac{\theta}{2} \mathbf{v}\right] $

4.3  转换关系

假定四元数 $q = s + x \mathbf{i} + y \mathbf{j} + z \mathbf{k}$，则旋转矩阵为

$\quad R = \begin{bmatrix}1-2(y^{2}+z^{2})&2(xy-sz)&2(xz+sy)\\2(xy+sz)&1-2(x^{2}+z^{2})&2(yz-sx)\\2(xz-sy)&2(yz+sx)&1-2(x^{2}+y^{2})\end{bmatrix} $

或另一种形式

$\quad R = \begin{bmatrix} s^2 + x^2 - y^2 -z^2 & 2(xy - sz) & 2(xz + sy) \\ 2(xy +sz) & s^2-x^2+y^2-z^2 & 2(yz - sx) \\ 2(xz-sy) & 2(yz+sx) & s^2-x^2-y^2+z^2 \end{bmatrix}$

附 - 欧拉角可视化

一个欧拉角的可视化链接 Euler Angle Visualization Tool，输入欧拉角可实时显示位姿变化

参考资料

《An Invitaton to 3D Vision》 ch2

《Robot Vision》ch13

OpenCV - 3D rigid/afine transforamtion

Understanding Quaternions

Rotation Matrix To Euler Angles

An Orge compatible class for euler angles