CF 672C 两个人捡瓶子 最短路与次短路思想

C. Recycling Bottles

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

It was recycling day in Kekoland. To celebrate it Adil and Bera went to Central Perk where they can take bottles from the ground and put them into a recycling bin.

We can think Central Perk as coordinate plane. There are n bottles on the ground, the i-th bottle is located at position (xi, yi). Both Adil and Bera can carry only one bottle at once each.

For both Adil and Bera the process looks as follows:

1. Choose to stop or to continue to collect bottles.
2. If the choice was to continue then choose some bottle and walk towards it.
3. Pick this bottle and walk to the recycling bin.
4. Go to step 1.

Adil and Bera may move independently. They are allowed to pick bottles simultaneously, all bottles may be picked by any of the two, it's allowed that one of them stays still while the other one continues to pick bottles.

They want to organize the process such that the total distance they walk (the sum of distance walked by Adil and distance walked by Bera) is minimum possible. Of course, at the end all bottles should lie in the recycling bin.

Input

First line of the input contains six integers ax, ay, bx, by, tx and ty(0 ≤ ax, ay, bx, by, tx, ty ≤ 109) — initial positions of Adil, Bera and recycling bin respectively.

The second line contains a single integer n (1 ≤ n ≤ 100 000) — the number of bottles on the ground.

Then follow n lines, each of them contains two integers xi and yi (0 ≤ xi, yi ≤ 109) — position of the i-th bottle.

It's guaranteed that positions of Adil, Bera, recycling bin and all bottles are distinct.

Output

Print one real number — the minimum possible total distance Adil and Bera need to walk in order to put all bottles into recycling bin. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct if .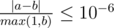

Examples

input

3 1 1 2 0 0

1 1
2 1
2 3

output

11.084259940083

input

5 0 4 2 2 0

5 2
3 0
5 5
3 5
3 3

output

33.121375178000

Note

Consider the first sample.

Adil will use the following path: .

Bera will use the following path: .

Adil's path will be 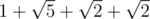 units long, while Bera's path will be 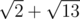units long.

题意：

C题题意：二维平面上有n个(n<=10^5)点(xi,yi)，有两个起点A(ax,ay)和B(bx,by)，一个终点T(tx,ty)(0<=横纵坐标<=10^9)

　　　　　可以从两个起点中的一个或两个出发，经过所有(xi,yi)，且每到达一个(xi,yi)都要回到终点，问所有走过距离的最小值

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <algorithm>
#include <set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define MM(a,b) memset(a,b,sizeof(a));
const double eps = 1e-;
const int  inf =0x7f7f7f7f;
const double pi=acos(-);
const int maxn=+;

struct point{
   double x,y;
}p[maxn];
point a,b,o;
int a1,a2,b1,b2;
double l[maxn+],mina,minb,seca,secb,ca1,ca2,cb1,cb2;

double dis(point a,point b)
{
   return pow((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y),0.5);
}

void solvea(int i)
{
    if(l[i]-dis(a,p[i])>mina)
    {
        seca=mina;
        ca2=ca1;
        mina=l[i]-dis(a,p[i]);
        ca1=i;
    }
    else if(l[i]-dis(a,p[i])>seca)
    {
        seca=l[i]-dis(a,p[i]);
        ca2=i;
    }
}

void solveb(int i)
{
    if(l[i]-dis(b,p[i])>minb)
    {
        secb=minb;
        cb2=cb1;
        minb=l[i]-dis(b,p[i]);
        cb1=i;
    }
    else if(l[i]-dis(b,p[i])>secb)
    {
        secb=l[i]-dis(b,p[i]);
        cb2=i;
    }
}

int main()
{
   while(~scanf("%lf %lf %lf %lf %lf %lf",&a.x,&a.y,&b.x,&b.y,&o.x,&o.y))
   {
       mina=minb=seca=secb=-1e20;
       ca1=,ca2=,cb1=,cb2=;
       int n;double ans=;

       scanf("%d",&n);
       for(int i=;i<=n;i++)
       {
           scanf("%lf %lf",&p[i].x,&p[i].y);
           l[i]=dis(p[i],o);
           ans+=*l[i];
           solvea(i);
           solveb(i);
       }

       if(ca1!=cb1)
           {
               if(mina<||minb<)
                  ans-=max(mina,minb);//刚开始没有加这句就wa了，因为即使两人最优的瓶子不是同
//一个,却可能存在其中有人的收益为负的情况，这种情况下就应该取两者中收益较大的一个（满足至少一个，可以///只有一个）
               else
                  ans-=mina+minb;
           }
       else
       {
           if(mina<||minb<)
               ans-=max(mina,minb);
           else
           {
             if(mina+max(secb,0.0)>minb+max(seca,0.0))
                ans-=mina+max(secb,0.0);
             else ans-=minb+max(seca,0.0);
           }
       }
       printf("%.16f\n",ans);
   }
   return ;
}

分析：用图论里的最短路和次短路的思想记录下最短路和次短路就好，，其实写的有点挫，可以直接用pair<double,int>再sort排序就好，，最关键的是，，要分情况讨论，因为两个人至少有一个要去捡，也就是说可以只有一个，所以应分情况讨论，错误点见代码