[20190727NOIP模拟测试9]单(single) 题解(树上dp)

啊啊啊啊啊啊啊啊考场上差一点就A掉了5555

千里之堤溃于蚁穴……鬼知道最后一步那么显然的柿子我为什么没考虑用上……

观察数据范围可知，出题人期望我们想出一个$O(n)$的做法

当然也有可能是$O(nlogn)$，但是这道题所求的数值与树上每个点的权值有关，

似乎用点分治并不能够解决。

那怎么办？树形dp啊。保证严格$O(n)$。

有了这样的思路，我们先来看第一问，并设计一个可以用一遍dfs计算出数组$b[]$的算法。

各位想必知道，树形dp的基本思想是$"Up\ and\ Down"$，

而在最近的比赛和专题中，我们似乎见的大部分这类问题都是先向下dfs到底，再从下往上更新父亲的$dp[]$信息。

但是不要忘了另外一种啊喂……这题先不说从下往上能不能转移，就是起始更新点的初值你都没法$O(n)$以内算……

如果从上往下，用父亲更新儿子就十分好考虑了。

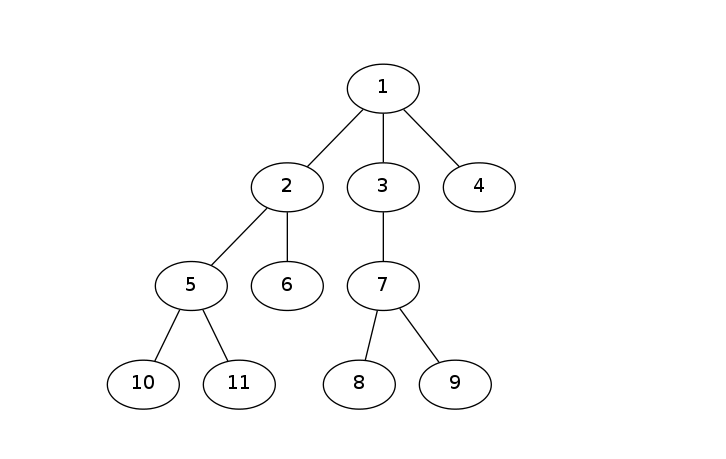
首先，起始点即为根节点，初值用一遍dfs即可算出。

之后考虑怎么转移。假设我们已知$b[2]$，要求它的儿子5的$b[]$，

这时候先来想一下$O(n^2)$的做法，即对于每个节点都跑一遍dfs，它究竟输在了哪里？

显然，有边相连的两点的$b[]$是有关系的，可以通过某种方式转化，而不必每次遍历整棵树进行冗余计算。

从2到5，5的子树(包含5本身)对于$b[]$的贡献都少了1，而5的子树之外的部分对它的贡献都多了1，

再通俗一点，我们把5的子树的贡献写出来：$b[2]=a_5+2*a_{10}+2*a_{11}...(之后就是5的子树之外的部分)$

而$b[5]=a_5*0+1*a_{10}+1*a_{11}+...$

看见没有？系数都少了1！子树外的部分同理。

那么一棵子树的贡献可以看作它内部点的权值和，第一遍dfs的时候就能预处理完毕。设它为$sum[]$。

易得:$b[y]=b[x]-sum[y]+sum[1]-sum[y]=b[x]+sum[1]-sum[y]*2$

第一问解决。

得出上面那个式子之后，第二问也就非常显然了。

我们把$b[x]$移到左侧，得到$b[y]-b[x]=sum[1]-sum[y]*2$

设$dt[y]=b[y]-b[x]$，这玩意相当于题里已经给了可以马上算出来。(当然$dt[1]$肯定求不出来)

先求出每个点的$dt[y]=sum[1]-sum[y]*2$,之后想怎么能够消元。

显然，$b[1]=\sum \limits _{i=2}^{n} sum[i]$

什么？并不显然？自己手玩去！

然后我们令$total=\sum \limits _{i=2}^{n}{dt[i]}=(n-1)sum[1]-2*\sum \limits_{i=2}^{n}{sum[i]}$

发现了什么？因为$b[1]$是已知量，所以可以把$total$减号后面的部分消掉！

$sum[1]$就求出来辣！

又因为所有的$dt[]$都是已知的，所有的$sum[]$就都可以求出来了。

至于$a[]$?再来一遍dfs就行了。

不得不说这道题真的很棒，没有特别难的知识点，整体难度也不太高，

但是很考验选手对于树上信息的处理能力和转化能力，以及基本的数学素养。

部分分也给的很合理，还能考察一下高斯消元。

还在犹豫什么？还不快来%%%% @liu_runda (逃

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int N=;
typedef long long ll;
int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<='')x=x*+ch-'',ch=getchar();
    return x*f;
}
int to[N<<],nxt[N<<],tot,head[N],num[N],sum[N],dep[N];
int dt[N];
int T,n,op;
int dp[N];
void add(int x,int y)
{
    to[++tot]=y;
    nxt[tot]=head[x];
    head[x]=tot;
}
void pre(int x,int deep)
{
    sum[x]=num[x];dep[x]=deep;
    for(int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(dep[y]||y==)continue;
        pre(y,deep+);
        sum[x]+=sum[y];
    }
}
void dfs(int x)
{
    for(int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(dep[y]<dep[x])continue;
        dp[y]=dp[x]-sum[y]+sum[]-sum[y];
        dfs(y);
    }
}
void DFS(int x,int f)
{
    for(int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(y==f)continue;
        dt[y]=dp[y]-dp[x];
        DFS(y,x);
    }
}
void cacl()
{
    for(int i=;i<=n;i++)
        num[i]=read();
    pre(,);
    for(int i=;i<=n;i++)
        dp[]+=dep[i]*num[i];
    dfs();
    for(int i=;i<=n;i++)
        printf("%d ",dp[i]);
    printf("\n");
}
void getans(int x,int f)
{
    ll ssum=;
    for(int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(y==f)continue;
        getans(y,x);
        ssum+=sum[y];
    }
    num[x]=sum[x]-ssum;
}
void solve()
{
    for(int i=;i<=n;i++)
        dp[i]=read();
    DFS(,);
    ll total=;
    for(int i=;i<=n;i++)
        total+=1LL*dt[i];
    sum[]=1LL*(dp[]*+total)/(n-);
    for(int i=;i<=n;i++)
        sum[i]=(-dt[i]+sum[])/;
    getans(,);
    for(int i=;i<=n;i++)
        printf("%d ",num[i]);
    printf("\n");
}
void ini()
{
    for(int i=;i<=n*;i++)
    {
        to[i]=nxt[i]=;
        if(i<=n)dp[i]=dt[i]=head[i]=sum[i]=num[i]=dep[i]=;
    }
    tot=;
}
void work()
{
    n=read();
    ini();
    for(int i=;i<n;i++)
    {
        int x=read(),y=read();
        add(x,y);add(y,x);
    }
    op=read();
    if(op)solve();
    else cacl();
}
int main()
{
    T=read();
    while(T--)work();
    return ;
}

UPD:附赠两组样例

Sample

两组是对称的（一组输入为另一组输出）