Kosaraju与Tarjan(图的强连通分量)

Kosaraju

这个算法是用来求解图的强连通分量的，这个是图论的一些知识，前段时间没有学，这几天在补坑...

强连通分量：

有向图中，尽可能多的若干顶点组成的子图中，这些顶点都是相互可到达的，则这些顶点成为一个强连通分量

如下图所示，a、b、e以及f、g和c、d、h各自构成一个强联通分量

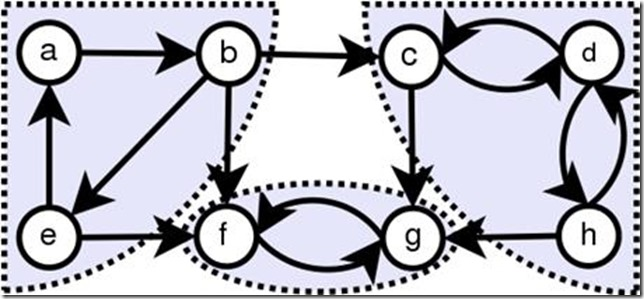
Kosaraju的求解方法

对于一个无向图的连通分量，从连通分量的任意一个顶点开始进行一次DFS，一定是可以遍历这个连通分量的所有定点的。所以，整个图的连通分量数就等价于我们对于这个图找了几次起点(也就是我们遍历这个图了几次DFS)。在这其中我们每一次遍历中所得到的定点属于同一个连通分量。

我们从无向图来推向有向图：

我们为了求得这个图的强联通分量，我们就需要对其进行DFS遍历，而顺序正遍历的DFS的过程是显然的，我们仍需要一种遍历顺序来满足可以达到我们可以使得每一个强联通分量都可以被遍历到且遍历的顺序是有序的算法。

逆后序遍历:

DFS的逆后序遍历指的是假如到达了A节点且A节点并没有被访问过，就去遍历与A节点相连的且没有被访问的其他节点，然后将这些节点假如栈中，最后这个栈从栈顶到栈底的顺序DFS逆后序遍历。

Kosaraju的步骤过程

对于任意的两个强联通分量之间是不可能存在有两条路互相连接形成环的(这是显然的，因为如果有环我们即需要将其看成是同一个强联通分量)。

所以求解的步骤可以分为以下两步：

第一步:

对原图取反，从任意一个顶点开始对反向图进行逆后续DFS遍历

第二步:

按照逆后续遍历中栈中的顶点出栈顺序，对原图进行DFS遍历，一次DFS遍历中访问的所有顶点都属于同一强连通分量。

证明算法的正确性：

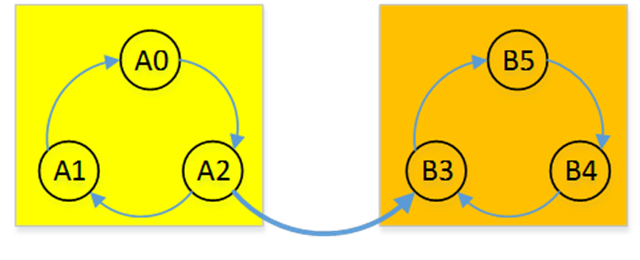
假设这一个图是需要求解强联通分量的图

那么对于这个图进行取反就得到了这个图: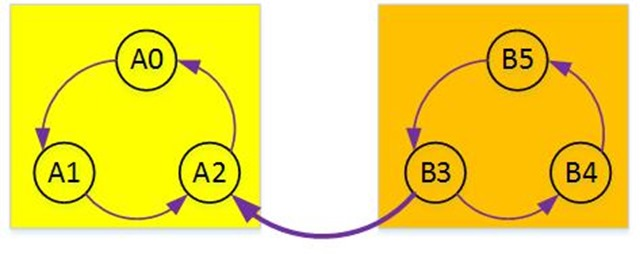

一共有两种DFS的可能性：

从A点开始:

假设DFS从位于强连通分量A中的任意一个节点开始。那么第一次DFS完成后，栈中全部都是强连通分量A的顶点，第二次DFS完成后，栈顶一定是强连通分量B的顶点。

从B点开始:

假设DFS从位于强连通分量B中的任意一个顶点开始。显然我们只需要进行一次DFS就可以遍历整个图，由于是逆后续遍历，那么起始顶点一定最后完成，所以栈顶的顶点一定是强连通分量B中的顶点。

所以对于每一次DFS，都会有一个对应的强联通分量，证毕

Code:

void dfsone(int x)
{
    vst[x] = ;
    for(int i=;i<=n;i++)
    if(!vst[i] && map[x][i])
    dfsone(i);
    d[++t] = x;  //最后访问的节点
}
  //d[i] = x : i -> 组  x -> 节点 

void dfstwo(int x)
{
    vst[x] = t;
    for(int i=;i<=n;i++)
    if(!vst[i] && map[i][x])
    dfstwo(i);
}

void kosaraju()
{
    int t = ;
    for(int i=;i<=n;i++)
    if(!vst[i])
    dfsone(i);
    memset(vst,,sizeof(vst));
    t = ;
    for(int i=n;i>=;i--)
    if(!vst[d[i]])
    {
        t++;
        dfstwo(d[i]);
    }
}

以上就是Kosaraju

接下来开始Tarjan

Tarjan

Tarjan是一种基于DFS的算法 ,图中每个强连通分量为搜索树的一棵子树

我们在DFS的过程中会遇到四种边:

树枝边:一条经过的边，即DFS搜索树上的一条边

前向边:与DFS方向一致，从某个节点指向其子孙的边

后向边:与DFS方向相反，从某个节点指向其祖先的边
横叉边:从某个节点指向搜索树中另一子树的某节点的边

定义一下:

DFN[i]:在DFS中该节点被搜索的次序(时间戳)

LOW[i]:为i或i的子树能够追溯到的最早的栈中节点的次序号

那么我们就可以显然地得到:

如果(u,v)为树枝边，u为v的父节点，则 LOW[u] = min(LOW[u],LOW[v])

如果(u,v)为后向边或者是指向栈中节点的横叉边，则 LOW[u] = min(LOW[u],DFN[v])

当节点u的搜索过程结束后，如果当DFN[ i ]==LOW[ i ]时，为i或i的子树可以构成一个强连通分量。

算法过程:

以1为Tarjan 算法的起始点，如图

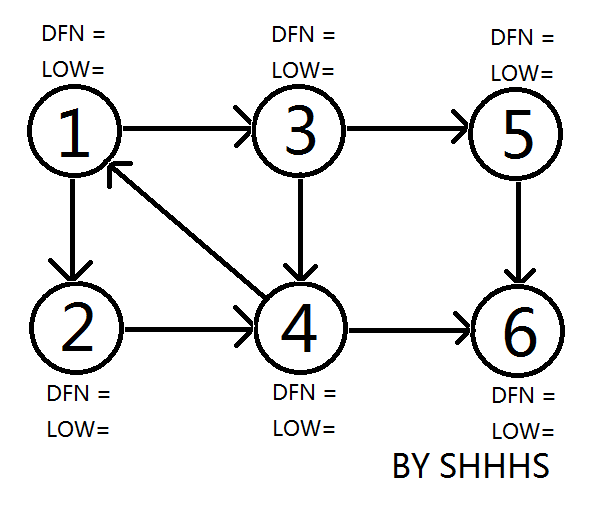
顺次DFS搜到节点6

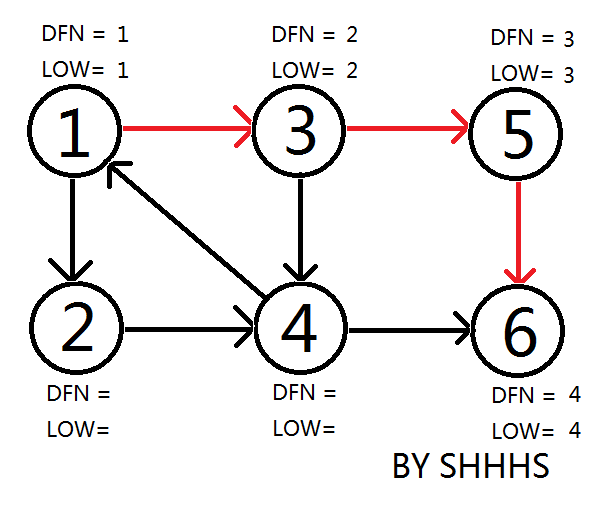
回溯时发现LOW[ 5 ]==DFN[ 5 ] ,  LOW[ 6 ]==DFN[ 6 ] ,则{ 5 } , { 6 } 为两个强连通分量。回溯至3节点，拓展节点4.

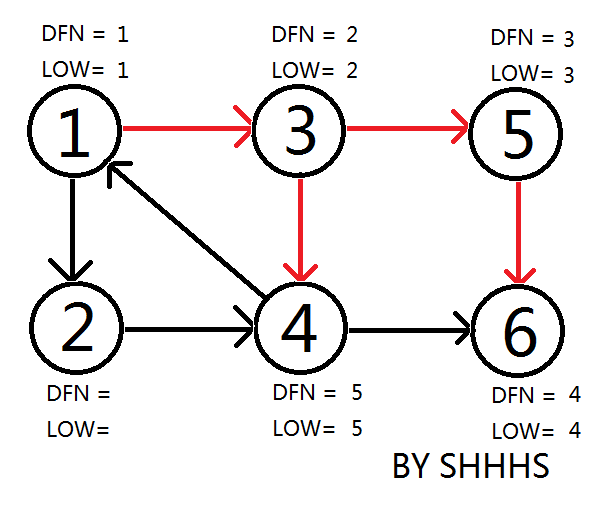
拓展节点1 ， 发现1再栈中更新LOW[ 4 ]，LOW[ 3 ] 的值为1

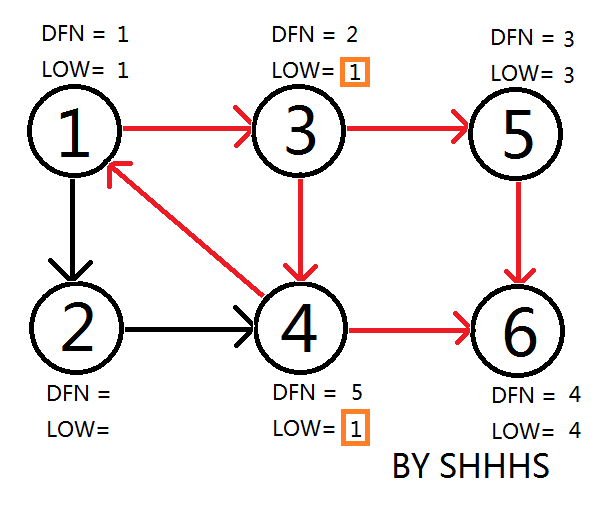
回溯节点1，拓展节点2

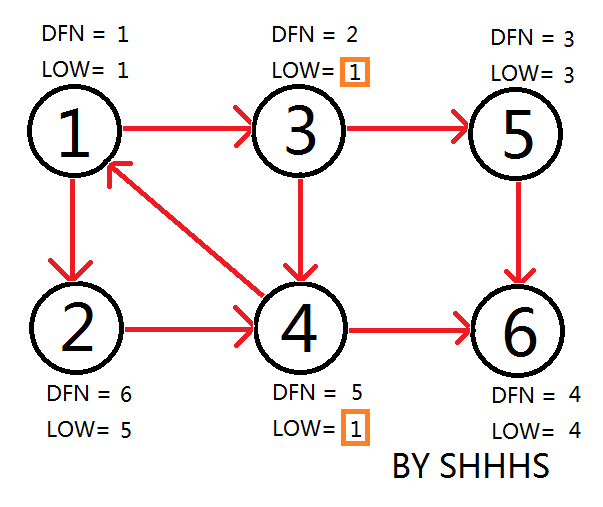
自此，Tarjan Algorithm 结束，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 为图中的三个强连通分量。

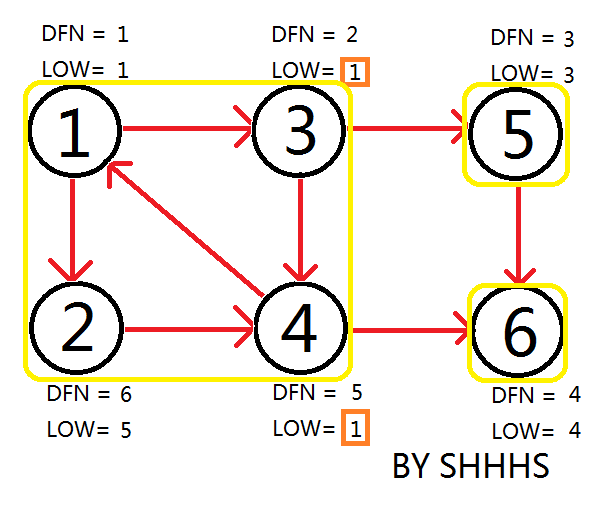
不难发现，Tarjan Algorithm 的时间复杂度为O(E+V).

Code:

void tarjan(int x)
{
    dfn[u] = low[u] = ++num;
    st[++top] = u;
    for(int i=fir[u];i;i=nex[i])
    {
        int v = to[i];
        if(!dfn[i])
        {
            tarjan(v);
            low[u] = min(low[u],low[v]);
        }
        else
        if(! co[v])
        low[u] = min(low[u],dfn[v]);
    }
    if(low[u] == dfn[u])
    {
        co[u] = ++col;
        while(st[top] != u)
        {
            co[st[top]] = col;
            top--;
        }
        top--;
    }
}