剑指offer： 数组中的逆序对

1. 最简单的思路，对每个值，遍历与其逆序的数组对；但时间复杂度太高；

2. 归并排序的思路：

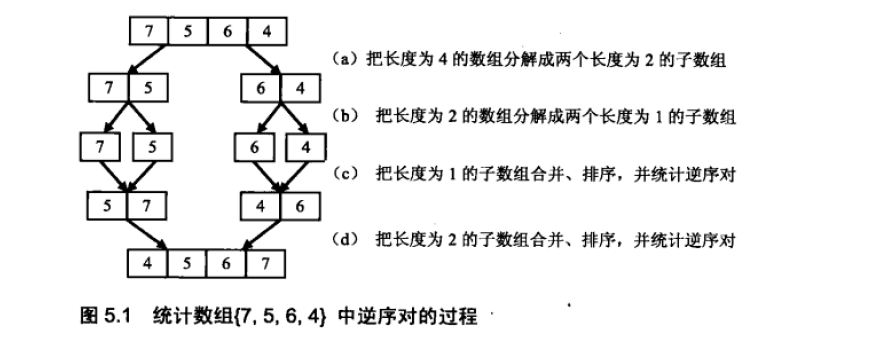
先将数组分隔成子数组，先统计出子数组内的逆序对的数目，然后统计两个相邻子数组之间的逆序对的数目；

    int InversePairsCore(int *data, int * copy, int start, int end)
    {
        //递归介绍条件，只剩一个元素
        if(start==end)
        {
            copy[start]=data[start];
            return ;
        }
        int length=(end-start)/;
        int left=InversePairsCore(copy, data, start, start+length);
        int right=InversePairsCore(copy,data, start+length+,end);
        int i=start+length;//前半段最后一个数字的下标
        int j=end;// 后半段最后一个下标
        int indexCopy=end;
        int count=;
        while(i>=start&& j>=start+length+)
        {
            if(data[i]>data[j])
            {
                copy[indexCopy--]=data[i--];
                count+=j-start-length;//右侧有j-start-length个元素，小于data[i]
              if(count>=)
                count%=;
            }
            else
            {

                copy[indexCopy--]=data[j--];//右侧元素大，，不存在逆序
            }

        }

        for(;i>=start;i--)
        {
            copy[indexCopy--]=data[i];
        }
        for(;j>=start+length+;j--)
        {
            copy[indexCopy--]=data[j];
        }
        return (left+right+count)%;
    }

    int InversePairs(int* data, int length)
    {

        if(data==NULL||length<)
        return ;
        int * copy=new int[length];
        for(int i=;i<length;++i)
        copy[i]=data[i];
        int count=InversePairsCore(data, copy,, length-);
        delete [] copy;
        return count;
    }