【codeforces 870F】Paths

Description

You are given a positive integer n. Let's build a graph on vertices 1, 2, ..., n in such a way that there is an edge between vertices u and v if and only if gcd(u,v)≠1. Let d(u, v) be the shortest distance between u and v, or 0 if there is no path between them. Compute the sum of values d(u, v) over all 1 ≤ u < v ≤ n.The gcd (greatest common divisor) of two positive integers is the maximum positive integer that divides both of the integers.

Input

Single integer n (1 ≤ n ≤ 107).

Output

Print the sum of d(u, v) over all 1 ≤ u < v ≤ n.

Examples

input

6

output

8

input

10

output

44

Note

All shortest paths in the first example:

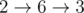
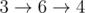
There are no paths between other pairs of vertices.The total distance is 2 + 1 + 1 + 2 + 1 + 1 = 8.

题意：

给定数字n，建立一个无向图。对于所有1~n之间的数字，当数字gcd(u,v)≠1时将u、v连一条边，边权为1。d(u, v)表示u到v的最短路，求所有d(u, v)的和，其中1 ≤ u < v ≤ n。

 

分析：

对于1以及所有大于n/2的的质数，与其他数字均不联通，直接剔除。

对于剩下的数字：

1.当gcd(u,v)≠1时，d(u, v)==1。即对于数字u，小于u且d(u, v)==1的数字个数为x - 1 - φ(x)。

2.令p[u]表示数字u的最小质因子，则当p[u]·p[v] ≤ n时，d(u, v)==2。维护数组num、sum，num[i]代表最小质因子为i的数字个数，sum数组为num数组的前缀和。统计Σnum[i]·sum[n/i]可以覆盖所有p[u]·p[v] ≤ n的情况，其中减去自身与自身被统计的情况，剩下的所有数对都被统计了两次，其中包含gcd(u,v)≠1的情况，需进行相应处理，详见代码。

3.剩下的数对最短路一定为3，因为 u→2·p[u]→2·p[v]→v这条路一定存在。可通过数对总数减去d(u, v)==1与d(u, v)==2的情况得到。

 

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define LL long long
 using namespace std;
 const int N=1e7+;
 int n,m,tot,now,pri[N],p[N],phi[N],num[N],sum[N];
 LL one,two,three;
 int main()
 {
     scanf("%d",&n);
     phi[]=;
     for(int i=;i<=n;i++)
     {
         if(!p[i]){p[i]=pri[++tot]=i;phi[i]=i-;}
         for(int j=;j<=tot;j++)
         {
             if(i*pri[j]>n)break;
             p[i*pri[j]]=pri[j];
             if(i%pri[j]==){phi[i*pri[j]]=phi[i]*pri[j];break;}
             else phi[i*pri[j]]=phi[i]*(pri[j]-);
         }
     }
     for(int i=;i<=n;i++)one+=i--phi[i];
     for(int i=;i<=n;i++)num[p[i]]++;
     for(int i=;i<=n;i++)sum[i]=sum[i-]+num[i];
     for(int i=;i<=n;i++)two+=1ll*num[i]*sum[n/i];
     for(int i=;i<=n;i++)if(1ll*p[i]*p[i]<=n)two--;
     two=two/-one;m=n-;
     for(int i=tot;i>=;i--)
         if(pri[i]*>n)m--;
         else break;
     three=1ll*m*(m-)/-one-two;
     printf("%I64d\n",one+two*+three*);
     return ;
 }