【Random Forest】林轩田机器学习技法

总体来说，林对于random forest的讲解主要是算法概况上的；某种程度上说，更注重insights。

林分别列举了Bagging和Decision Tree的各自特点：

Random Forest就是这二者的结合体。

1）便于并行化

2）保留了C&RT的优势

3）通过bagging的方法削弱了fully-grown tree的缺点

这里提到一个insights：如果各个分类器的diversity越大，aggregation之后的效果可能就越好。

因此，Random Forest不仅样本是boostrapping的，而且对于features的处理上也采用了类似的方式。

采用random subspace的好处就是：特征维度降低了，运算效率提高了。

更进一步，RF的作者又提出了一种延伸的思路：

任何一个low-dimension的feature空间都可以看成是由投影矩阵P对原来feature的变换，或者可以说对原features做了线性组合（combination）

一种特例就是：如果投影过后没有任何变化时，这个P就是natural basis。

RF的作者为了引入更多的randomness，建议在做每一次b(x)的时候，都考虑用投影矩阵来对features做变换。这样就真的是randomness everywhere了。

接下来，林介绍了如何针对RF的特点做模型Validation的问题。

首先，林给出了，在RF的每棵树的boostrapping的过程中，没有被用到（out-of-bag）的样本的比例大概是多少。

假设每棵树都boostrappingN次，那么还是会有1/3的样本是没有被这棵树抽中的。

对于每棵树来说，这些没有被boostrapping过程抽中的样本就叫Out-Of-Bag。

利用这种规律，RF模型的validation方式就有些飘逸了。

1）一种直观的验证思路是，用每棵树的OOB数据来验证gt；然并卵，RF模型并不看重每棵树的分类效果

2）第二种思路就来了，有点儿绕，但是也说得清（可以类比validation by one的验证方法）。

　　比如(x1,y1)这个数据，对于g2,g3是out of bag的，那么对于(x1,y1)这个样本的error，就可以用G(g2,g3)的average来验证。（如果只有（x1,y1)这一个点来验证，那就是validation by one的方法了）。

　　对于(x1,y1)~...(xN,yN)大部分都可以找到，以这些样本为OOG的G(gi...)，分别求这些validation的值，再取一个平均就OK了。

第二种验证思路：

　　a. 既保证了测试的数据绝对没有在训练时被偷窥

　　b. 保证了不是验证单棵子树gt，而是着眼于G(gi...)的表现

这种validation的方式在实际中非常好用，不用re-training，省时省力。

接下来进入了feature selection的议题。

这个议题其实也比较自然，既然Random Forest每一步都需要randomness选特征，自然就要问：哪些特征更important?

首先回顾了线性模型：

线性模型学习过程的结果W，本身就是对变量重要性的度量：|wi|越大（不论正负）都对结果影响比较大，因此也更重要。

还有一种统计学方法，就是用permutation test的思路来做。

比如N个样本，每个样本d维度特征，要想衡量其中第i维特征的重要性，可以把这N个样本的第i维特征都洗牌打乱。再评价洗牌前和洗牌后的模型performance。

但是这样就有一个问题，必须不断地洗牌、训练，过程很繁琐。

于是RF的作者想到一种有些偷懒的trick，如下：

训练的时候，不玩儿permutation了；改在validation的时候玩儿permutation了：即把OOB测试样本的xn,i打乱洗牌，再进行评估验证。

这个trcik也算上是一个非常pratical的想法吧，学习了。

最后，林列举了几个RF模型在实际中的例子：

1）对于简单的数据集，RF模型倾向于得到平滑，置信区间大的分类器

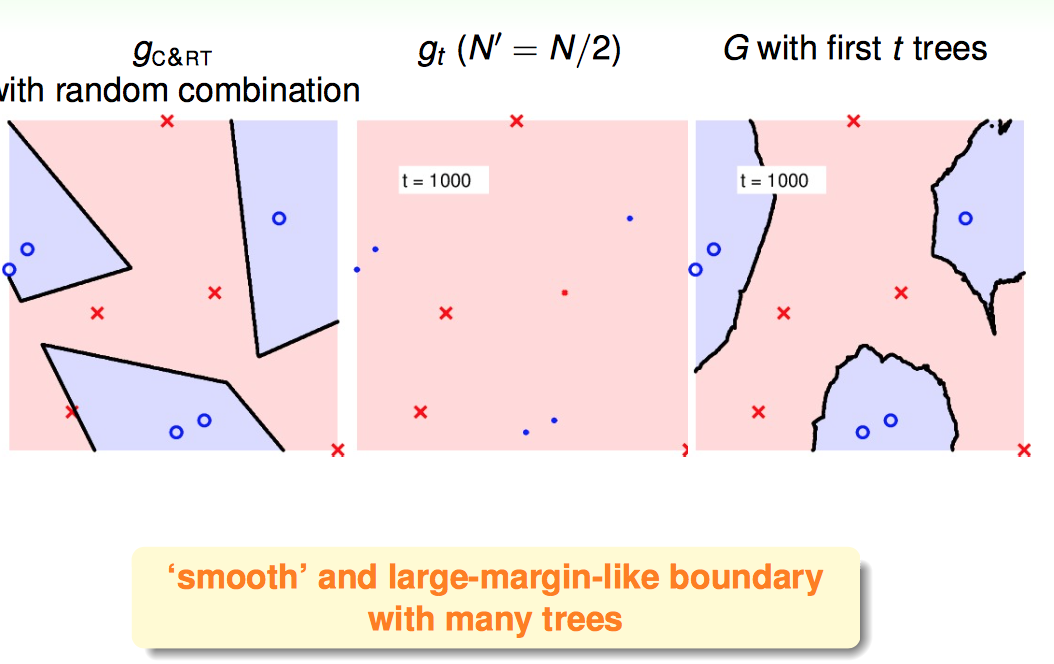
2）对于复杂有噪声的数据（决策树表现不好的），RF模型的降噪性很好

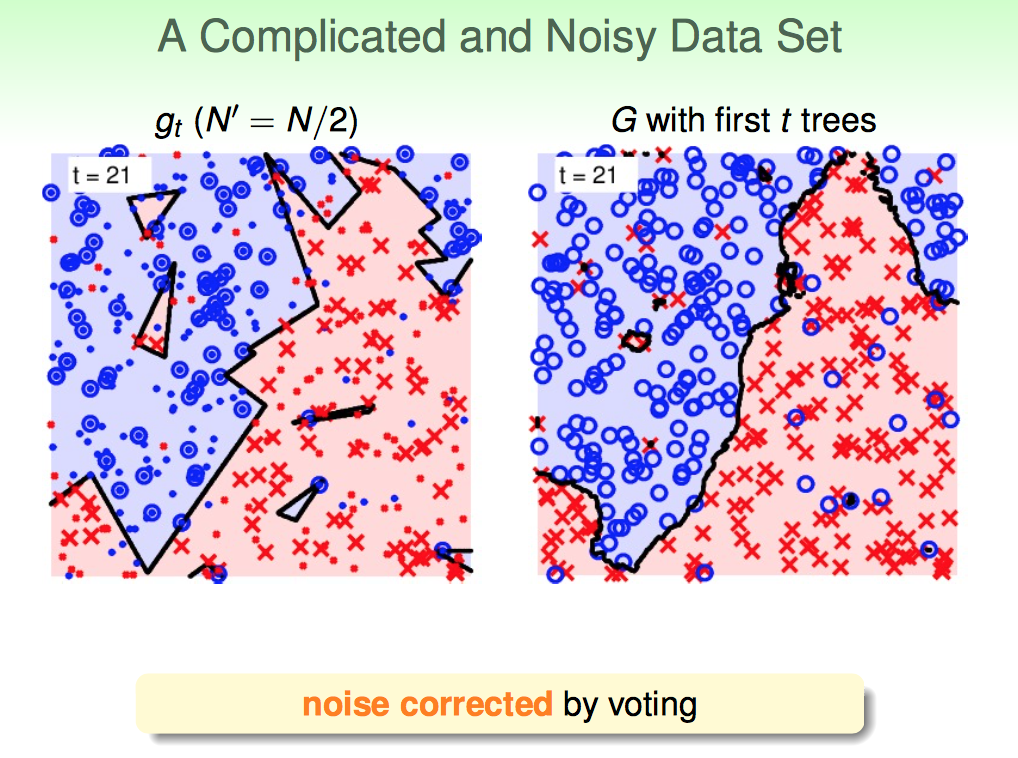
3）森林里选多少棵树比较好？

总之是树越多越好，但是由于是随机森林的，random seed也很重要（这个就要看缘分了）。