压缩感知重构算法之压缩采样匹配追踪（CoSaMP）

压缩采样匹配追踪(CompressiveSampling MP)是D. Needell继ROMP之后提出的又一个具有较大影响力的重构算法。CoSaMP也是对OMP的一种改进，每次迭代选择多个原子，除了原子的选择标准之外，它有一点不同于ROMP：ROMP每次迭代已经选择的原子会一直保留，而CoSaMP每次迭代选择的原子在下次迭代中可能会被抛弃。

在这之前先读了下参考论文[1]，论文前面还是看得懂一点的，讲了一些压缩感知的基础知识，还聊到了压缩重构方法主要分为三类，但是到了第2部分介绍算法的时候又看不懂了，感觉符号都还没聊清楚就开始讲流程了。佩服看得懂的博主，还说很容易就看懂了。。。希望自己好好努力也能看懂这些外文文献，fighting啦！

那么我先把论文中的流程贴出来，并没有对符号作过多的解释。。。  supp(x)表示x的支撑集

          

然后在网上找到了符合论文中符号的代码。

function Sest = cosaomp(Phi,u,K,tol,maxiterations)
Sest = zeros(size(Phi,2),1);
v = u;
t = 1;
numericalprecision = 1e-12;
T = [];
while (t <= maxiterations) && (norm(v)/norm(u) > tol)
  y = abs(Phi'*v);
  [vals,z] = sort(y,'descend');
  Omega = find(y >= vals(2*K) & y > numericalprecision);
  T = union(Omega,T);
  b = pinv(Phi(:,T))*u;
  [vals,z] = sort(abs(b),'descend');
  Kgoodindices = (abs(b) >= vals(K) & abs(b) > numericalprecision);
  T = T(Kgoodindices);
  Sest = zeros(size(Phi,2),1);
  phit = Phi(:,T);
  b = pinv(phit)*u;
  Sest(T) = b;
  v = u - phit*b;
  t = t+1;
end

接下来综合代码我准备强行解释一波论文算法的伪代码流程，哎呀半懂半懂希望以后要全懂全懂。

1.Identification（识别）

大意是说要构造一个signal proxy，在伪代码中构造signal proxy是y=Phi*v，下图是从论文中摘出来的，突然明白了这段话的意思，首先翻译一下。信号重构的最大难点在于找到目标信号中这些最大项所在的位置。CoSaOMP受到RIP的启发，假设字典矩阵的RIP常数为远远小于1的一个值，对s稀疏的信号x，y=Phi*Phi x可以作为信号的一个代理。因为y的每一个s向量的结合的能量与信号x中s个向量的能量相对应。（我觉得这里的Phi应该是理解为字典矩阵的，因为计算内积的时候我们是选择将字典矩阵与残差相乘，残差初始化为观测向量也就是Phi*x）。这一步对应着代码的第8行。

接着是伪代码中所说的Identify large components，也就是找到内积值中最大的2K项，复制给Ω，对应上述代码的第10行。

2.Support Merger（合并支撑集）

代码第11行。

3.Estimation

这里是求解一个最小二乘问题，pinv是求伪逆矩阵。

“b|Tc←0”中的“Tc”应该是T的补集(complementary set)，向量b的元素序号为全集，子集T对应的元素等于最小二乘解，补集对应的元素为零。

4.Pruning（修剪）

代码第13行，选出b中K个最大项。

5.Sample Update（更新）

---

强行解释结束了，接下来贴出博主的解释。

1、CoSaMP重构算法流程

步骤（5）稍微有点绕，综合代码理解一下还是不难的。

2、压缩采样匹配追踪(CoSaOMP)Matlab代码(CS_CoSaMP.m)

function [ theta ] = CS_CoSaMP( y,A,K )
%CS_CoSaOMP Summary of this function goes here
%Created by jbb0523@@2015-04-29
%Version: 1.1 modified by jbb0523 @2015-05-09
%   Detailed explanation goes here
%   y = Phi * x
%   x = Psi * theta
%   y = Phi*Psi * theta
%   令 A = Phi*Psi, 则y=A*theta
%   K is the sparsity level
%   现在已知y和A，求theta
%   Reference:Needell D，Tropp J A．CoSaMP：Iterative signal recovery from
%   incomplete and inaccurate samples[J]．Applied and Computation Harmonic
%   Analysis，2009，26：301-321.
    [y_rows,y_columns] = size(y);
    if y_rows<y_columns
        y = y';%y should be a column vector
    end
    [M,N] = size(A);%传感矩阵A为M*N矩阵
    theta = zeros(N,1);%用来存储恢复的theta(列向量)
    Pos_theta = [];%用来迭代过程中存储A被选择的列序号
    r_n = y;%初始化残差(residual)为y
    for kk=1:K%最多迭代K次
        %(1) Identification
        product = A'*r_n;%传感矩阵A各列与残差的内积
        [val,pos]=sort(abs(product),'descend');
        Js = pos(1:2*K);%选出内积值最大的2K列
        %(2) Support Merger
        Is = union(Pos_theta,Js);%Pos_theta与Js并集
        %(3) Estimation
        %At的行数要大于列数，此为最小二乘的基础(列线性无关)
        if length(Is)<=M
            At = A(:,Is);%将A的这几列组成矩阵At
        else%At的列数大于行数，列必为线性相关的,At'*At将不可逆
            if kk == 1
                theta_ls = 0;
            end
            break;%跳出for循环
        end
        %y=At*theta，以下求theta的最小二乘解(Least Square)
        theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解
        %(4) Pruning
        [val,pos]=sort(abs(theta_ls),'descend');
        %(5) Sample Update
        Pos_theta = Is(pos(1:K));
        theta_ls = theta_ls(pos(1:K));
        %At(:,pos(1:K))*theta_ls是y在At(:,pos(1:K))列空间上的正交投影
        r_n = y - At(:,pos(1:K))*theta_ls;%更新残差
        if norm(r_n)<1e-6%Repeat the steps until r=0
            break;%跳出for循环
        end
    end
    theta(Pos_theta)=theta_ls;%恢复出的theta
end

3、CoSaMP单次重构测试代码

以下测试代码基本与OMP单次重构测试代码一样。

%压缩感知重构算法测试
clear all;close all;clc;
M = 64;%观测值个数
N = 256;%信号x的长度
K = 12;%信号x的稀疏度
Index_K = randperm(N);
x = zeros(N,1);
x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的，且位置是随机的
Psi = eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi = randn(M,N);%测量矩阵为高斯矩阵
A = Phi * Psi;%传感矩阵
y = Phi * x;%得到观测向量y
%% 恢复重构信号x
tic
theta = CS_CoSaMP( y,A,K );
x_r = Psi * theta;% x=Psi * theta
toc
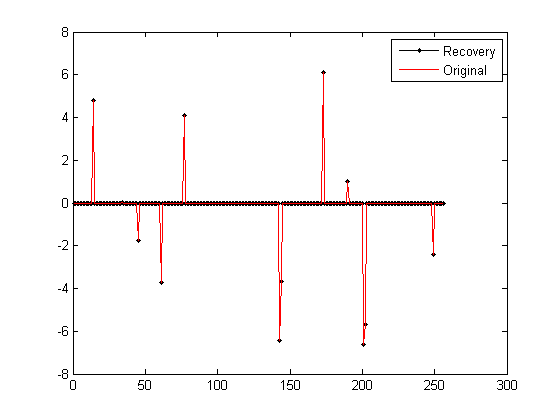
%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x)%恢复残差

运行结果如下：（信号为随机生成，所以每次结果均不一样）

 1）图：

2）Command  windows

      Elapsedtime is 0.073375 seconds.

      恢复残差：

      ans=

          7.3248e-015

4、测量数M与重构成功概率关系曲线绘制例程代码

以下测试代码基本与OMP测量数M与重构成功概率关系曲线绘制代码一样。增加了“fprintf('K=%d,M=%d\n',K,M);”，可以观察程序运行进度。

clear all;close all;clc;
%% 参数配置初始化
CNT = 1000;%对于每组(K,M,N)，重复迭代次数
N = 256;%信号x的长度
Psi = eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
K_set = [4,12,20,28,36];%信号x的稀疏度集合
Percentage = zeros(length(K_set),N);%存储恢复成功概率
%% 主循环，遍历每组(K,M,N)
tic
for kk = 1:length(K_set)
    K = K_set(kk);%本次稀疏度
    M_set = 2*K:5:N;%M没必要全部遍历，每隔5测试一个就可以了
    PercentageK = zeros(1,length(M_set));%存储此稀疏度K下不同M的恢复成功概率
    for mm = 1:length(M_set)
       M = M_set(mm);%本次观测值个数
       fprintf('K=%d,M=%d\n',K,M);
       P = 0;
       for cnt = 1:CNT %每个观测值个数均运行CNT次
            Index_K = randperm(N);
            x = zeros(N,1);
            x(Index_K(1:K)) = 5*randn(K,1);%x为K稀疏的，且位置是随机的
            Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵
            A = Phi * Psi;%传感矩阵
            y = Phi * x;%得到观测向量y
            theta = CS_CoSaMP(y,A,K);%恢复重构信号theta
            x_r = Psi * theta;% x=Psi * theta
            if norm(x_r-x)<1e-6%如果残差小于1e-6则认为恢复成功
                P = P + 1;
            end
       end
       PercentageK(mm) = P/CNT*100;%计算恢复概率
    end
    Percentage(kk,1:length(M_set)) = PercentageK;
end
toc
save CoSaMPMtoPercentage1000 %运行一次不容易，把变量全部存储下来
%% 绘图
S = ['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
for kk = 1:length(K_set)
    K = K_set(kk);
    M_set = 2*K:5:N;
    L_Mset = length(M_set);
    plot(M_set,Percentage(kk,1:L_Mset),S(kk,:));%绘出x的恢复信号
    hold on;
end

本程序运行结果：

最后摘出文献[4]中关于ROMP优缺点的分析：

ROMP 算法虽具有贪婪算法的速度以及凸优化算法的强有力的理论保证，但其与StOMP 算法一样，对稀疏度K 的依赖性太大，稀疏度估计的准确与否，将会影响到算法的收敛性、收敛速度、鲁棒性以及重构信号的性能。针对此缺点，提出了正则化自适应匹配追踪( Regularized adaptive matching pursuit，RAMP) 算法，该算法将ROMP 算法进行改进，引入回溯的思想，自适应调节候选集原子的数目。

CoSaMP 算法为了提高算法的收敛速度和算法效率，通过回溯的思想从原子库里选择多个相关原子同时剔除部分不相关原子。设算法的迭代步长为K，候选集中最多有3K 个原子，每次最多剔除K个原子，以保证支撑集中有2K 个原子。CoSaMP 算法虽结合了组合算法的思想保证了算法的收敛速度，而且提供了严格的误差界，但其与ROMP 算法一样需要已知信号的稀疏度K。然而实际应用中的信号往往是近似稀疏的，其稀疏度K需要去估计。如果低估了K 的值，算法精确重构的能力会下降甚至可能会消除，导致算法不再收敛;若高估了K 的值，算法的鲁棒性和重构精度都将会下降，使得重构的信号的误差增大，导致最终重构得到的信号失真。此外，CoSaMP 算法每步迭代时增加与剔除原子所依据的原则不一样，增加原子时依据的是原子与余量的相关性原则，剔除原子时依据的是重构信号的大小，标准的不同可能会导致对支撑集的估计不准确。针对第一个问题，仍可以采取改变信号的稀疏度，多次运行，使得重构精度最高的稀疏度即作为信号的稀疏度的思想，也可以引入回溯思想自适应选择原子。针对第二个问题，可以改变剔除原子的标准，采用依据原子与余量的相关性原则，剔除相关性小的原子，使得每步迭代时增加与剔除原子所依据的标准一样。

 

参考文献：

[1]D. Needell, J.A. Tropp．CoSaMP: Iterative signal recoveryfrom incomplete and inaccurate samples.http://arxiv.org/pdf/0803.2392v2.pdf

[2]D.Needell, J.A. Tropp．CoSaMP: Iterative signal recoveryfrom incomplete and inaccurate samples[J]. Communications of theACM，2010，53(12)：93-100.

(http://dl.acm.org/citation.cfm?id=1859229)

[3] 彬彬有礼.压缩感知重构算法之压缩采样匹配追踪(CoSaMP).http://blog.csdn.net/jbb0523/article/details/45441361

[4] 杨真真，杨震，孙林慧.信号压缩重构的正交匹配追踪类算法综述[J]. 信号处理，2013，29(4)：486-496.