pcl曲面重建模块-poisson重建算法示例

poisson曲面重建算法

ｐｃｌ-1.8测试通过

#include <iostream>
#include <pcl/common/common.h>
#include <pcl/io/pcd_io.h>
#include <pcl/io/ply_io.h>
#include <pcl/search/kdtree.h>
#include <pcl/features/normal_3d_omp.h>
#include <pcl/point_types.h>
#include <pcl/surface/mls.h>
#include <pcl/surface/poisson.h>
#include <pcl/filters/passthrough.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <boost/thread/thread.hpp>

using namespace pcl;
using namespace std;

int
main (int argc, char** argv)
{

        /*点云读入阶段*/
        if(argc <= 2) {
                cout << "请输入点云数据文件名称，并指定输出数据文件名称" << endl;
                return 1;      

        }
        PointCloud<PointXYZ>::Ptr cloud (new PointCloud<PointXYZ>);
        if(io::loadPCDFile<PointXYZ> (argv[1], *cloud) == -1){
                cout << "数据读入失败！！" << endl;

                return 1;
        }
        cout << "数据读入　　　完成" << endl;

        /*滤波阶段*/
        PointCloud<PointXYZ>::Ptr filtered(new PointCloud<PointXYZ>());
        PassThrough<PointXYZ> filter;
        filter.setInputCloud(cloud);
        filter.filter(*filtered);
        cout << "低通滤波　　　完成" << endl;

        // MovingLeastSquares<PointXYZ, PointXYZ> mls;
        // mls.setInputCloud(filtered);
        // mls.setSearchRadius(0.01);
        // mls.setPolynomialFit(true);
        // mls.setPolynomialOrder(2);
        // mls.setUpsamplingMethod(MovingLeastSquares<PointXYZ, PointXYZ>::SAMPLE_LOCAL_PLANE);
        // mls.setUpsamplingRadius(0.005);
        // mls.setUpsamplingStepSize(0.003);

        // PointCloud<PointXYZ>::Ptr cloud_smoothed (new PointCloud<PointXYZ>());
        // mls.process(*cloud_smoothed);
        // cout << "移动最小二乘平面滤波完成" << endl;

        /*法向计算阶段*/
        NormalEstimationOMP<PointXYZ, Normal> ne;
        ne.setNumberOfThreads(8);
        ne.setInputCloud(filtered);
        ne.setRadiusSearch(5);
        Eigen::Vector4f centroid;
        compute3DCentroid(*filtered, centroid);
        ne.setViewPoint(centroid[0], centroid[1], centroid[2]);

        PointCloud<Normal>::Ptr cloud_normals (new PointCloud<Normal>());
        ne.compute(*cloud_normals);

        for(size_t i = 0; i < cloud_normals->size(); ++i){
                cloud_normals->points[i].normal_x *= -1;
                cloud_normals->points[i].normal_y *= -1;
                cloud_normals->points[i].normal_z *= -1;
        }

        PointCloud<PointNormal>::Ptr cloud_smoothed_normals(new PointCloud<PointNormal>());
        //将点云数据的坐标和法向信息拼接
        concatenateFields(*filtered, *cloud_normals, *cloud_smoothed_normals);

        cout << "法向计算　　　完成" << endl;

        /*poission 重建阶段*/
        //创建poisson重建对象
        Poisson<PointNormal> poisson;
        // poisson.setDepth(9);
        //输入poisson重建点云数据
        poisson.setInputCloud(cloud_smoothed_normals);
        //创建网格对象指针，用于存储重建结果
        PolygonMesh mesh;
        //poisson重建开始
        poisson.reconstruct(mesh);

        //将重建结果存储到硬盘，并保存为PLY格式
        io::savePLYFile(argv[2], mesh);
        cout << "曲面重建　　　完成" << endl;

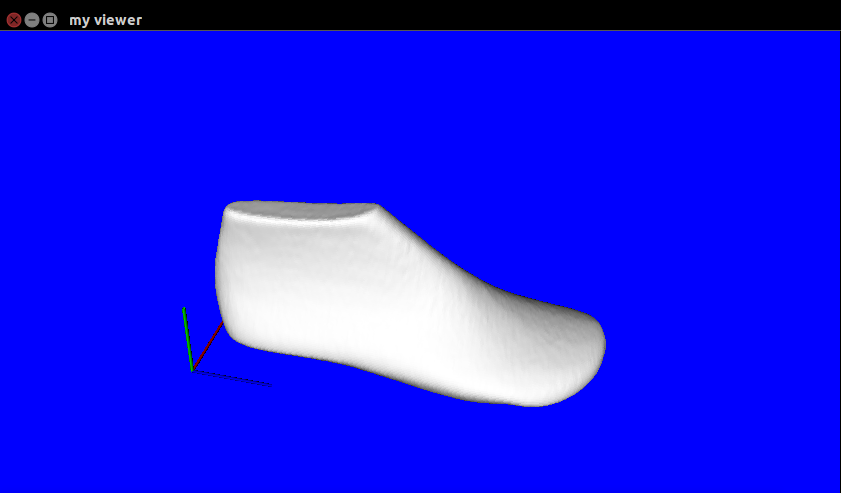
        /*图形显示阶段*/
        cout << "开始图形显示......" << endl;
        boost::shared_ptr<pcl::visualization::PCLVisualizer>viewer(new pcl::visualization::PCLVisualizer("my viewer"));

        viewer->setBackgroundColor(0,0,7);
        viewer->addPolygonMesh(mesh, "my");
        viewer->addCoordinateSystem(50.0);
        viewer->initCameraParameters();

        while(!viewer->wasStopped()){

                viewer->spinOnce(100);
                boost::this_thread::sleep(boost::posix_time::microseconds(100000));
        }

        return (0);
}