洛谷P3768 简单的数学题

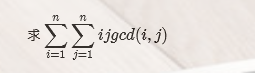
解：

神奇的一批......参观yyb巨神的博客。

大致思路就是第一步枚举gcd，发现后面有个限制是gcd=1，用反演，得到的F(x)是两个等差数列求积。

然后发现有个地方我们除法的除数是乘积，于是换元枚举那个乘积。提到最前面。

稍微化一下，发现后面有个Id * miu，这个东西化成phi。

然后得到一个式子，前半部分是s²(n/i)这个整除分块，后面就要相应的求这个东西i²phi[i]的前缀和来迎合整除分块。

然后就是杜教筛，先设个g，把h(n)写出来发现要消掉一个d²，于是g(x) = x²。

没了。

 #include <cstdio>
 #include <map>

 typedef long long LL;
 const int N = , T = ;

 LL MO;

 inline LL qpow(LL a, LL b) {
     LL ans = ;
     while(b) {
         if(b & ) ans = ans * a % MO;
         a = a * a % MO;
         b = b >> ;
     }
     return ans;
 }

 std::map<LL, LL> mp;
 int p[N], top, phi[N];
 LL F[N], inv2, inv6;
 bool vis[N];

 inline void getp(int n) {
     phi[] = ;
     for(int i = ; i <= n; i++) {
         if(!vis[i]) {
             p[++top] = i;
             phi[i] = i - ;
         }
         for(int j = ; j <= top && i * p[j] <= n; j++) {
             vis[i * p[j]] = ;
             if(i % p[j] == ) {
                 phi[i * p[j]] = phi[i] * p[j];
                 break;
             }
             phi[i * p[j]] = phi[i] * (p[j] - );
         }
     }
     for(int i = ; i <= n; i++) {
        F[i] = (F[i - ] + (1ll * i * i % MO * phi[i] % MO)) % MO;
     }
     return;
 }

 inline LL s2(LL x) { /// sum[1~n] ^ 2
     x %= MO;
     LL temp = (x + ) * x /  % MO;
     return temp * temp % MO;
 }

 inline LL H(LL x) { /// sum of n^3
     return s2(x);
 }

 inline LL G(LL x) { /// sum of n^2
     x %= MO;
     return (x <<  | ) % MO * (x + ) % MO * x % MO * inv6 % MO;
 }

 LL getF(LL x) {
     if(x <= ) return ;
     if(x <= T) return F[x];
     if(mp.count(x)) return mp[x];
     LL ans = H(x);
     for(LL i = , j; i <= x; i = j + ) {
         j = x / (x / i);
         ans -= (G(j) - G(i - ) + MO) % MO * getF(x / i) % MO;
         ans = (ans % MO + MO) % MO;
     }
     return mp[x] = ans;
 }

 int main() {
     LL n;
     scanf("%lld%lld", &MO, &n);
     getp(T);
     inv6 = qpow(, MO - );
     inv2 = (MO + ) / ;

     LL ans = ;
     for(LL i = , j; i <= n; i = j + ) {
         j = n / (n / i);
         ans += s2(n / i) * (getF(j) - getF(i - ) + MO) % MO;
         ans = (ans % MO + MO) % MO;
     }
     printf("%lld\n", ans);
     return ;
 }

AC代码