hdu多校第4场 B Harvest of Apples（莫队）

Problem B. Harvest of Apples
 
Time Limit: / MS (Java/Others)    Memory Limit: / K (Java/Others)
Total Submission(s):     Accepted Submission(s): 
 
Problem Description
There are n apples on a tree, numbered from  to n.
Count the number of ways to pick at most m apples.
 
Input
The first line of the input contains an integer T (≤T≤) denoting the number of test cases.
Each test case consists of one line with two integers n,m (≤m≤n≤).
 
Output
For each test case, print an integer representing the number of ways modulo +.
 
Sample Input
 
Sample Output
 
Source
 Multi-University Training Contest 
 
Recommend
chendu   |   We have carefully selected several similar problems for you:       

求C(n,0)+C(n,1)+C(n,2)+.....+C(n,m);

设S(n,m)=C(n,0)+C(n,1)+C(n,2)+.....+C(n,m);

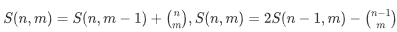
第一个式子易得，第二个式子：杨辉三角的 n,m=(n-1,m)+(n-1,m-1)

那么就是这一行等于上一行的都用了2次，只有第最后一个用了一次

所以减去c（n-1，m）

#include<iostream>
#include<stdio.h>
#include<cmath>
#include<algorithm>
using namespace std;
const int mod=1e9+7;
#define ll long long
const int maxn=1e5+7;
ll jiecheng[maxn],inv[maxn];
ll ans[maxn];
int block;
ll qsm(ll a,ll b)
{
    ll ans=1;
    while(b){
        if(b&1)
            ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}
void init()
{
    jiecheng[1] = 1;
    for(int i = 2; i < maxn; i++)
        jiecheng[i] = jiecheng[i-1] * i % mod;
    for(int i = 1; i < maxn; i++)
        inv[i] = qsm(jiecheng[i], mod-2);
}
struct node{
    int l,r;
    int i;
}modui[maxn];
bool cmp(node a,node b)
{
    if(a.l/block==b.l/block)
        return a.r<b.r;
    return a.l<b.l;
}
ll C(ll n,ll m)
{
 
    if(m == 0 || m == n) return 1;
    ll ans=1;
    ans=(jiecheng[n]*inv[m])%mod*inv[n-m];
    ans=ans%mod;
    return ans;
}
int main()
{
    init();
    block = sqrt(maxn);
    int t;
    scanf("%d",&t);
    for(int i=0;i<t;i++)
    {
        scanf("%d%d",&modui[i].l,&modui[i].r);
        modui[i].i=i;
    }
    sort(modui,modui+t,cmp);
    int l=1,r=0;
    int sum=1;
    for(int i = 0; i < t; i++)
    {
        while(l < modui[i].l) sum = (2 * sum - C(l++, r) + mod) % mod;
        while(l > modui[i].l) sum = ((sum + C(--l, r))*inv[2]) % mod;
        while(r < modui[i].r) sum = (sum + C(l, ++r)) % mod;
        while(r > modui[i].r) sum = (sum - C(l, r--) + mod) % mod;
        ans[modui[i].i] = sum;
    }
    for(int i=0;i<t;i++)
    {
        printf("%lld\n",ans[i]);
    }
 
    return 0;
}