算法实践--最小生成树（Prim算法）

前一篇介绍了一种最小生成树的算法--Kruskal算法，本篇介绍另一种Prim算法

算法描述

定义V为端点的集合，A为最小生成树，初始为空。对于每个端点v初始的Key[v]=∞, Parent[v]=null

初始化Q为V, 指定任意一个端点为root，其值Key[r]=0

while(Q不为空) {

　　找出Q中Key值最小的u

　　Q = Q - u

　　if (PARENT[u] != null) {

　　　　将(u, Parent(u))加入A中

　　}

　　foreach(u的相邻端点v) {

　　　　if (v在Q中且w(u, v) < Key[v]) {

　　　　PARENT[v] = u;

　　　　Key[v] = w;

　　}

}

return A

图片示例

初始状态

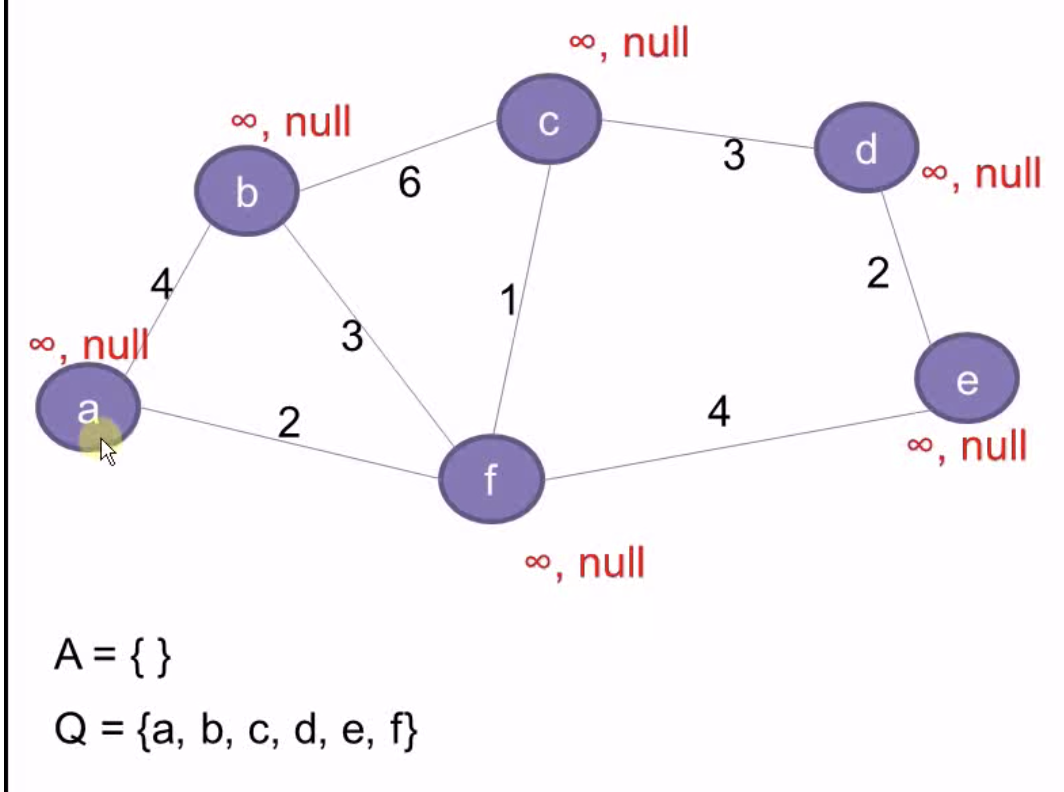
选择一个端点a作为root

找出Q中Key最小的a，将其从Q中删除，同时更新其相邻端点b和f的Key和PARENT

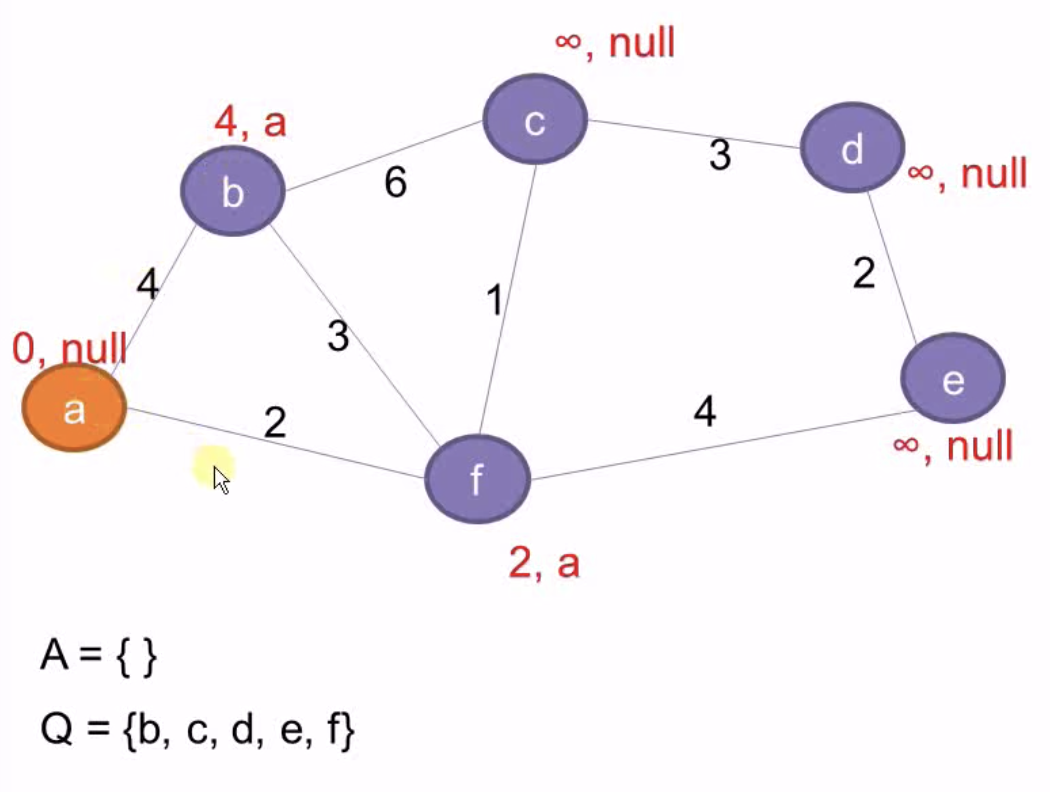
找出Q中Key最小的f， 从Q中删除，因为f的父节点为a，将(a, f)加到A中。同时更新f相邻节点的Key和父节点

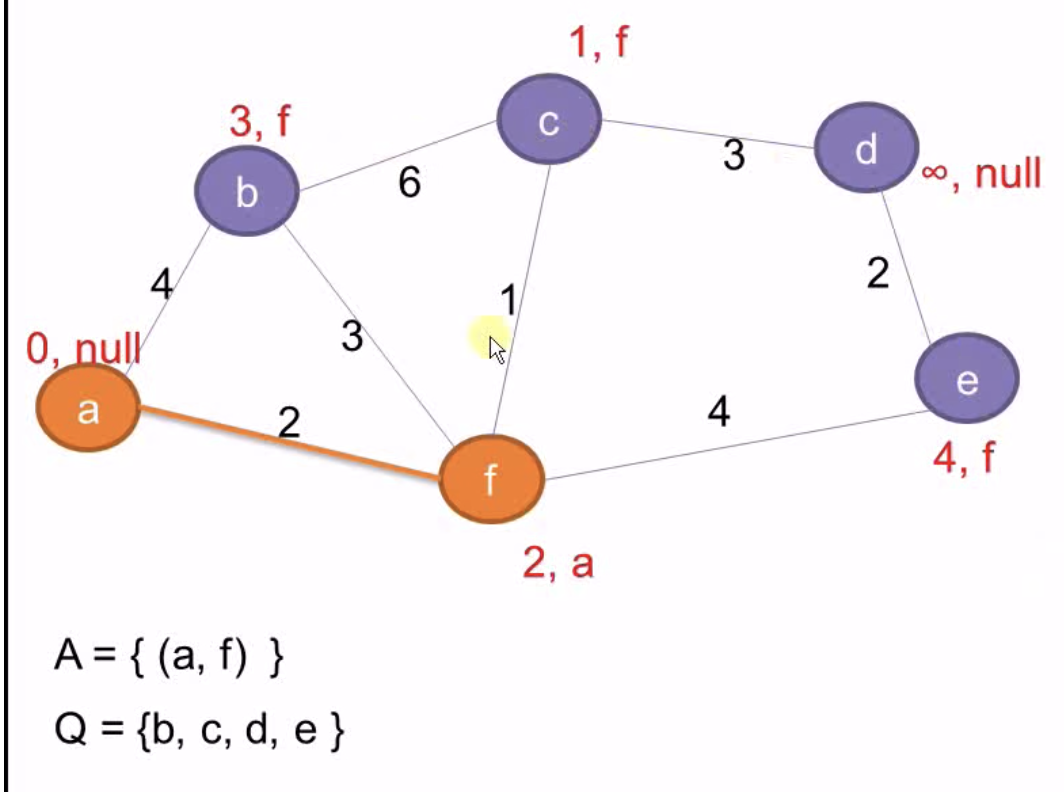
Q减去c，A加上(c ,f)， 更新相邻节点d的Key和父节点

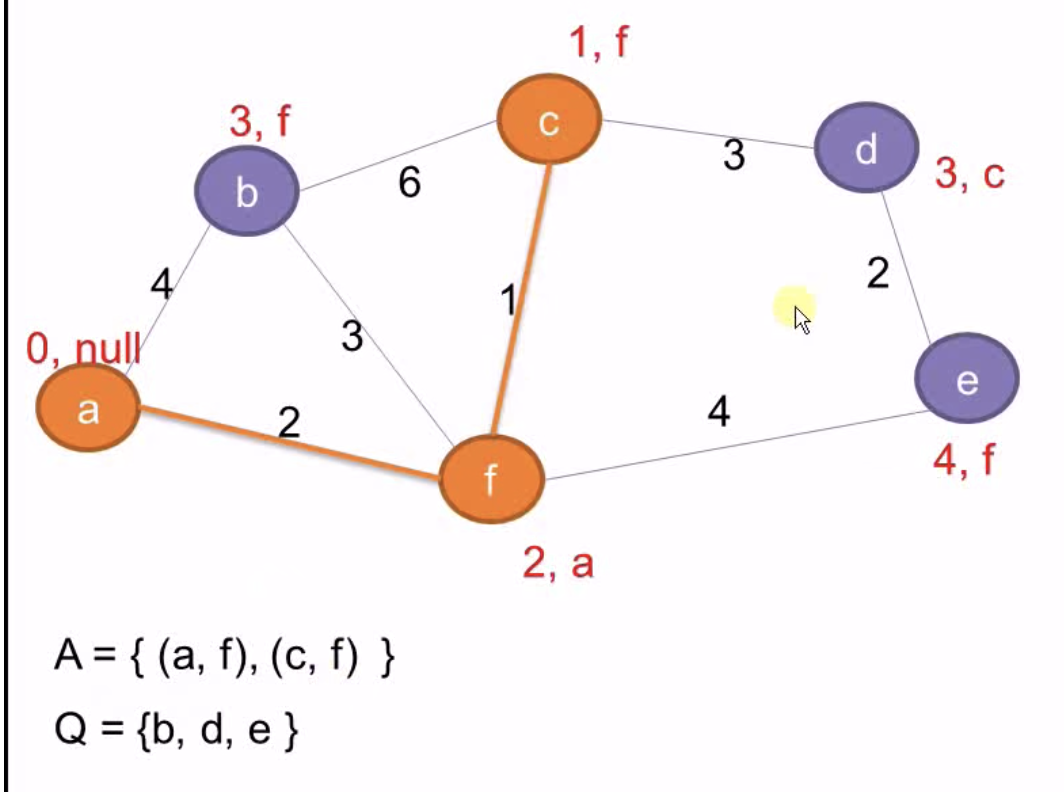
Q减去b，A加上(b, f)

Q减d，A加(c, d)

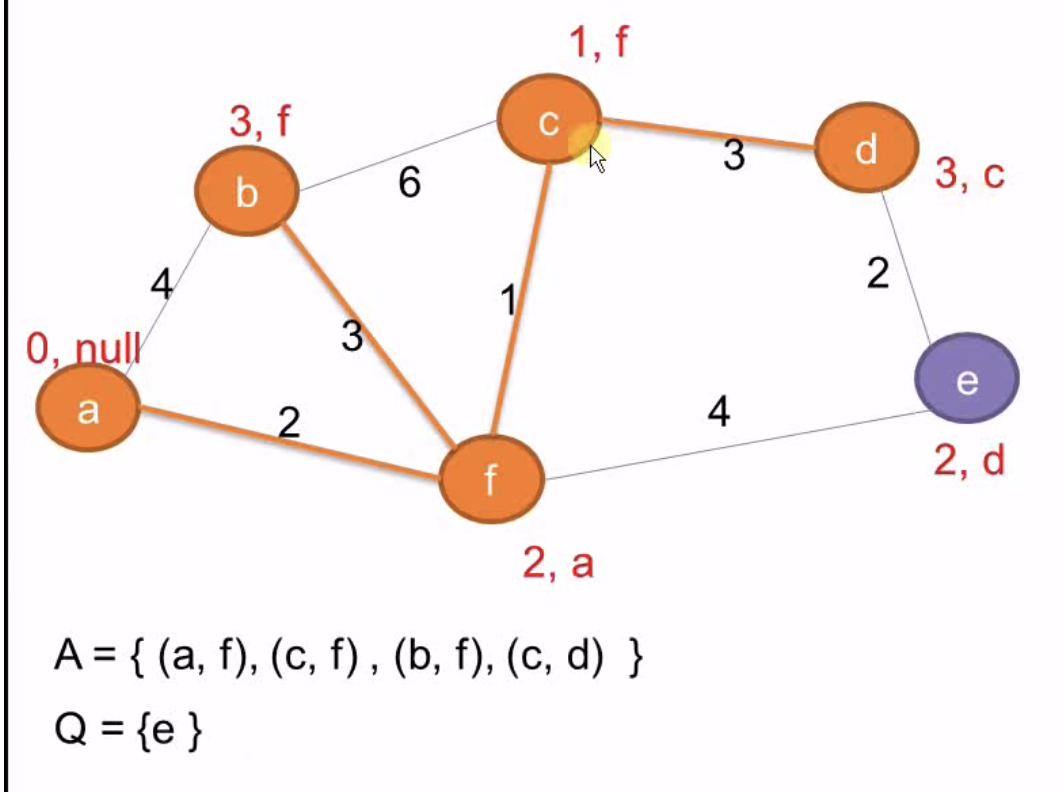
Q减e，A加(d, e)

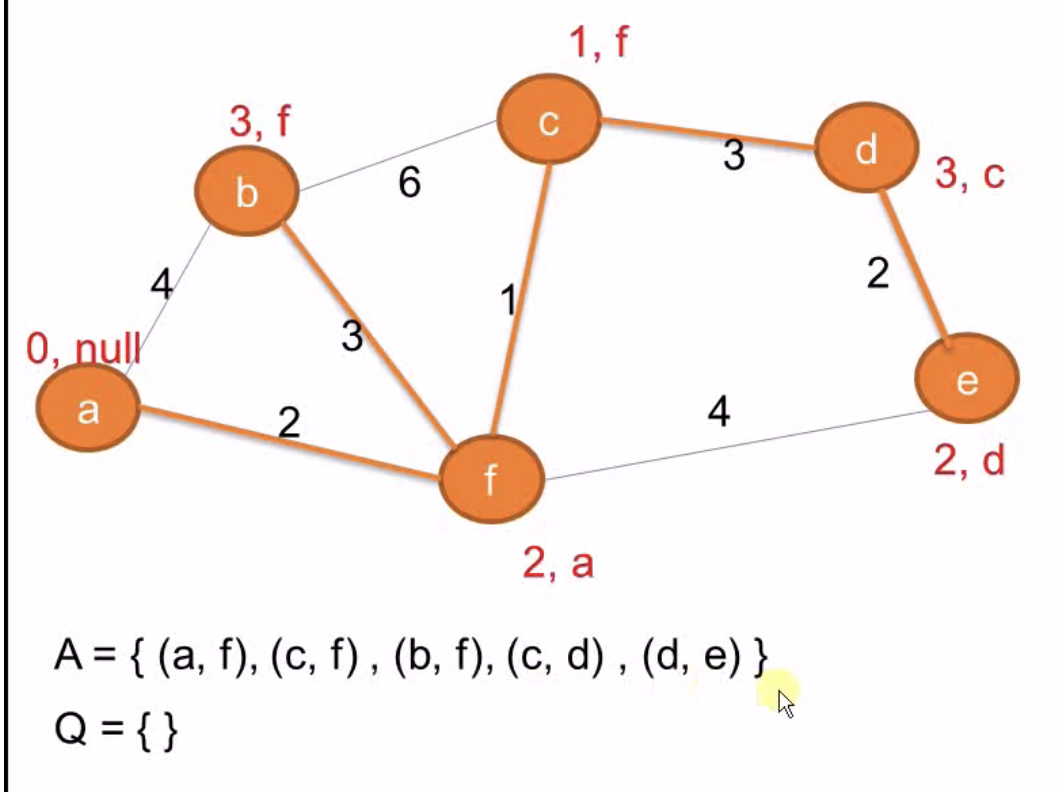
C++代码实现

struct Edge {
    char vertex1;
    char vertex2;
    int weight;
    Edge(char v1, char v2, int w):vertex1(v1), vertex2(v2), weight(w) {}
};

struct Graph {
    vector<char> vertice;
    vector<Edge> edges;
    vector< pair<char, Edge> > adjacent(char u) {　　// 返回端点u所有相邻的端点及权重
        vector< pair<char, Edge> > res;
        for (Edge e : edges) {
            if (e.vertex1 == u) {
                res.push_back( make_pair(e.vertex2, e));
            } else if (e.vertex2 == u) {
                res.push_back( make_pair(e.vertex1, e));
            }
        }
        return res;
    }
};

void prim(Graph& g, char root) {
    unordered_map<char, char> res;
    unordered_map<char, char> PARENT;
    unordered_map<char, int> KEY;

    for (auto c : g.vertice) {
        PARENT[c] = '\0';
        KEY[c] = INT_MAX;
    }
    KEY[root] = ;
    vector<char> Q = g.vertice; 

    while (!Q.empty()) {    // O(V)
        char u = *std::min_element(Q.begin(), Q.end(), [&](char x, char y) {return KEY[x] < KEY[y];});  // O(v)
        vector<char>::iterator itr = remove(Q.begin(), Q.end(), u);  // O(V)
        Q.erase(itr, Q.end());  // erase() following remove() idiom
        if (PARENT[u] != '\0') {
            res[u] = PARENT[u];   // This is one edge of MST
        }
        vector< pair<char, Edge> > adj = g.adjacent(u);   // O(E)
        for (pair<char, Edge> v : adj) {
            if (find(Q.begin(), Q.end(), v.first) != Q.end()) {   // O(V)
                if (v.second.weight < KEY[v.first]) {
                    PARENT[v.first] = u;
                    KEY[v.first] = v.second.weight;
                }
            }
        }
    }

    for (auto e : res) {
        cout << e.first << " -- " << e.second << endl;
    }
}

int main() {

    Graph g;

    char t[] = {'a', 'b', 'c', 'd', 'e', 'f'};
    g.vertice = vector<char>(t, t + sizeof(t)/sizeof(t[]));

    g.edges.push_back(Edge('a', 'b', ));
    g.edges.push_back(Edge('a', 'f', ));
    g.edges.push_back(Edge('f', 'b', ));
    g.edges.push_back(Edge('c', 'b', ));
    g.edges.push_back(Edge('c', 'f', ));
    g.edges.push_back(Edge('f', 'e', ));
    g.edges.push_back(Edge('d', 'e', ));
    g.edges.push_back(Edge('d', 'c', ));

    prim(g, 'a');

    return ;
}