字符串匹配的 Boyer-Moore 算法

上一篇文章，我介绍了 字符串匹配的KMP算法

但是，它并不是效率最高的算法，实际采用并不多。各种文本编辑器的” 查找” 功能（Ctrl+F），大多采用 Boyer-Moore 算法。

下面，我根据 Moore 教授自己的例子来解释这种算法。

1.

假定字符串为”HERE IS A SIMPLE EXAMPLE”，搜索词为”EXAMPLE”。

2.

首先，” 字符串” 与” 搜索词” 头部对齐，从尾部开始比较。

这是一个很聪明的想法，因为如果尾部字符不匹配，那么只要一次比较，就可以知道前 7 个字符肯定不是要找的结果。

我们看到，”S” 与”E” 不匹配。这时，“S” 就被称为” 坏字符”（bad character），即不匹配的字符。我们还发现，”S” 不包含在搜索词”EXAMPLE” 之中，这意味着可以把搜索词直接移到”S” 的后一位。

3.

依然从尾部开始比较，发现”P” 与”E” 不匹配，所以”P” 是” 坏字符”。但是，”P” 包含在搜索词”EXAMPLE” 之中。所以，将搜索词后移两位，两个”P” 对齐。

4.

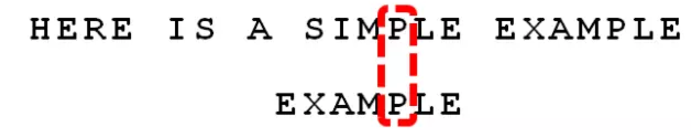
我们由此总结出 “坏字符规则”：

后移位数 = 坏字符的位置 – 搜索词中的上一次出现位置

如果” 坏字符” 不包含在搜索词之中，则上一次出现位置为 -1。

以”P” 为例，它作为” 坏字符”，出现在搜索词的第 6 位（从 0 开始编号），在搜索词中的上一次出现位置为 4，所以后移 6 – 4 = 2 位。再以前面第二步的”S” 为例，它出现在第 6 位，上一次出现位置是 -1（即未出现），则整个搜索词后移 6 – (-1) = 7 位。

5.

依然从尾部开始比较，”E” 与”E” 匹配。

6.

比较前面一位，”LE” 与”LE” 匹配。

7.

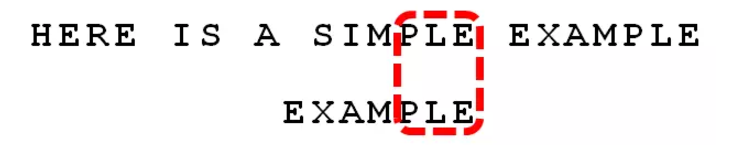
比较前面一位，”PLE” 与”PLE” 匹配。

8.

比较前面一位，”MPLE” 与”MPLE” 匹配。我们把这种情况称为” 好后缀”（good suffix），即所有尾部匹配的字符串。注意，”MPLE”、”PLE”、”LE”、”E” 都是好后缀。

9.

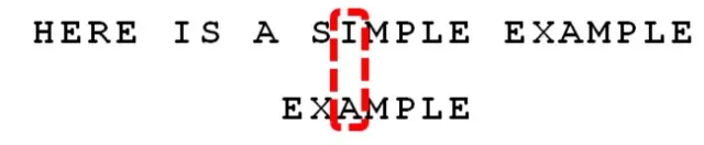
比较前一位，发现”I” 与”A” 不匹配。所以，”I” 是” 坏字符”。

10.

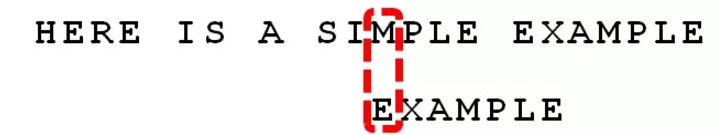
根据” 坏字符规则”，此时搜索词应该后移 2 – （-1）= 3 位。问题是，此时有没有更好的移法？

11.

我们知道，此时存在”好后缀”。所以，可以采用 “好后缀规则”：

后移位数 = 好后缀的位置 – 搜索词中的上一次出现位置

计算时，位置的取值以” 好后缀” 的最后一个字符为准。如果” 好后缀” 在搜索词中没有重复出现，则它的上一次出现位置为 -1。

所有的” 好后缀”（MPLE、PLE、LE、E）之中，只有”E” 在”EXAMPLE” 之中出现两次，所以后移 6 – 0 = 6 位。

12.

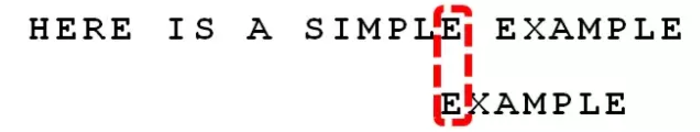
可以看到，” 坏字符规则” 只能移 3 位，” 好后缀规则” 可以移 6 位。所以，Boyer-Moore 算法的基本思想是，每次后移这两个规则之中的较大值。

更巧妙的是，这两个规则的移动位数，只与搜索词有关，与原字符串无关。因此，可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时，只要查表比较一下就可以了。

13.

继续从尾部开始比较，”P” 与”E” 不匹配，因此”P” 是” 坏字符”。根据” 坏字符规则”，后移 6 – 4 = 2 位。

14.

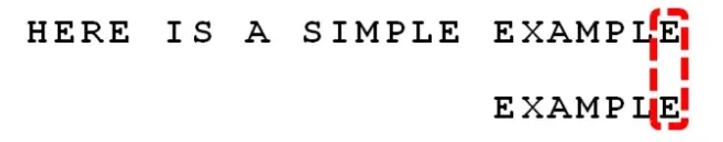
从尾部开始逐位比较，发现全部匹配，于是搜索结束。如果还要继续查找（即找出全部匹配），则根据” 好后缀规则”，后移 6 – 0 = 6 位，即头部的”E” 移到尾部的”E” 的位置。