[luogu5008]逛庭院

首先我们看到数据范围。妈耶！数据这么大，一开始还想用个DP来做，但是看着就不行，那么根据这个数据范围，我们大致可以猜到这道题的算法是一个贪心，那么我们怎么贪呢？

我们首先还是先画一个图：

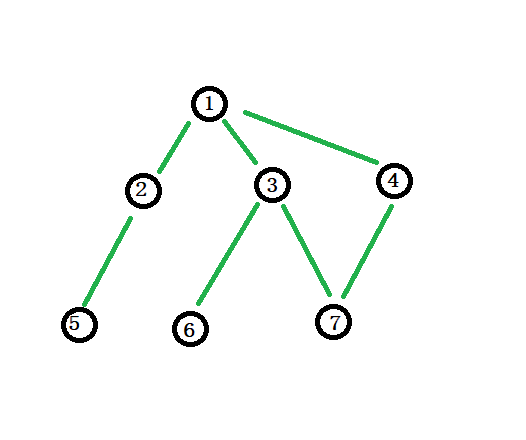
样例解释一下：

我们取的点是\(3\)，\(5\)，\(7\)。

看到题目，因为\(1\)号节点的入度为0，那么就一定不能选择\(1\)号节点，那么接下来可以供我们选择的最大的权值的点也就只有\(3\)，\(5\)，\(7\)号节点，那么我们就来一个贪心策略：对每一个节点的权值进行排序，然后将所有不能取的节点全部不算，剩下的就都取最大的那几个。

以下是\(30\)分骗分程序

# include <bits/stdc++.h>
# define Ri register int
# define for1(i,a,b) for(Ri i(a);i<=b;++i)
# define for2(i,a,b) for(Ri i(a);i>=b;--i)

using namespace std;

inline int read ()
{
    int w = 0,x = 0;
    char ch = 0;
    while (!isdigit(ch)) { w |= ch =='-'; ch = getchar();}
    while (isdigit(ch)) { x = (x<<1) + (x<<3) + (ch ^ 48); ch = getchar(); }
    return w ? -x : x;
}

const int Maxm = 2000004;
const int Maxn = 5000004;

int Nedge, n, m, k;
int head[Maxm], ind[Maxn];

struct node{
    int v ,id ,ind ;
}a[5000004];

bool cmp (node a,node b)
{
    return a.v > b.v;
}

int main()
{
    n = read(),m = read(),k = read(); Nedge = 1;
    for1(i ,1 ,n ) a[i].v = read(),a[i].id = i;
    for1(i ,1 ,m )
    {
        int u = read(),v = read();
        a[v].ind ++;
    }
    sort (a + 1 , a + 1 + n , cmp);
    int cnt = 0 , ans = 0;
    for1(i ,1 ,n)
    {
        if (a[i].ind == 0) continue;
        else
        {
            ans += a[i].v;
            cnt ++;
            if (cnt == k) break;
        }
    }
    printf ("%d\n", ans);
    return 0;
}

但是这个贪心一定是错的。

为什么

我们来想一下，如果可以去掉的节点，是某一个接下来可以取的节点的唯一一个入边来源，那么这个一定会影响后面的答案，这个点也就不取了，所以我们就不能这样做。

---

那么我们应该怎么做呢？

这个时候我们就需要 胆大心细地思考题目了。我是好好听了出征大会的

其实也就只需要在这个贪心的基础上，加上一个契机，这个契机就是让当前这个删去的点，可以不对后面的点产生影响。

正解策略是：我们首先缩点，然后找到入度为0的环，删去这个环中权值最小的点，然后从小到大排序，取前k大的点。

我们先给一个缩点的模板吧！

inline void tarjan(int u)
{
    dfn[u] = low[u] = ++ dep;
    vis[u] = 1;
    S[top++] = u;
    for (int i = head[u]; i != -1; i = edge[i].next )
    {
        int v = edge[i].to;
        if (!dfn[v])
        {
            tarjan(v);
            low[u] = Min(low[u] ,low[v]);
        }
        else if (vis[v]) low[u] = Min(low[u] ,low[v]);
    }
    int j;
    if (dfn[u] == low[u])
    {
        sum ++;
        do
        {
            j = S[ -- top];
            belong[j] = sum ;
            vis [j] = 0;
        }while (u != j) ;
    }
}

---

解释

那么我们就需要一个手段，使得这个这个点成为一个删去和不删去，不会影响答案得到东西：这个玩意的名字叫做缩点。

为什么我们会想到缩点，我们得从DAG中的环开始说起。

早在。。因为在有向图中，每一个点都是可以互相到达的，那么所以这个有向图中的每一个点都是有入度的，没有人反驳吧！，所以这个里面的点都是可以随意取的，但是要注意attention：当你这这个环是\(0\)的入度时，那么你就不能随意取掉最后一个点了，因为你这个最后一个点可能就没有入度了，那么我们为了保证所有的点都可以取到，我们就将这个环内的权值最小的点删去，那么这样就可以保证这个环断开后，这个点集中的点就可以随便取了。

那么还有一个问题，也就是如果是一个节点的缩点？

其实也是一个道理，我就不解释了，也就是把这个点删掉，反正这个点完全没有用。

---

以下是AC代码（新的码风本人感觉还是挺好看的QAQ）

# include <bits/stdc++.h>
# define Ri register int
# define for1(i,a,b) for(Ri i(a);i<=b;++i)
# define for2(i,a,b) for(Ri i(a);i>=b;--i)
# define ms(a,b) memset(a,b,sizeof(a))

using namespace std;

typedef long long LL;

const int M = 2000005;

struct Edge{
    int to ,next;
}edge[M];

int dfn[M], vis[M], low[M], S[M], head[M] ,belong[M] ,ind[M];
int dep, top, sum , n ,m ,k ,Nedge;

struct node{
    int v ,id ;
}a[M];

inline int read() //快读
{
    int w = 0,x = 0;
    char ch = 0;
    while (!isdigit(ch))
    {
        w |= ch == '-';
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x<<1) + (x<<3) + (ch^48);
        ch = getchar();
    }
    return w ? -x : x ;
}

inline int Min(int n,int m) //三目取min
{
    return n < m ? n : m;
}

inline void Add_Edge(int u ,int v) //链式前向星
{
    edge[Nedge] = (Edge) {v ,head[u]} ;
    head[u] = Nedge++;
}

inline void tarjan(int u) //tarjan缩点模板
{
    dfn[u] = low[u] = ++ dep;
    vis[u] = 1;
    S[top++] = u;
    for (int i = head[u]; i != -1; i = edge[i].next )
    {
        int v = edge[i].to;
        if (!dfn[v])
        {
            tarjan(v);
            low[u] = Min(low[u] ,low[v]);
        }
        else if (vis[v]) low[u] = Min(low[u] ,low[v]);
    }
    int j;
    if (dfn[u] == low[u])
    {
        sum ++;
        do
        {
            j = S[ -- top];
            belong[j] = sum ;
            vis [j] = 0;
        }while (u != j) ;
    }
}

inline bool cmp1(node a,node b) //从小到大排序
{
    return a.v < b.v;
}

inline bool cmp2(node a,node b) //从大到小排序
{
    return a.v > b.v;
}

int main()
{
    ms(head ,-1);
    ms(dfn ,0);
    ms(vis ,0);
    ms(belong ,0);
    sum = 0,dep = 0,top = 0;
    n = read(),m = read(),k = read();
    for1(i ,1 ,n) a[i].v = read(),a[i].id = i;
    for1(i ,1 ,m)
    {
        int u = read(),v = read();
        Add_Edge(u , v);
    }
    for1(i ,1 ,n)
    {
        if (!dfn[i]) tarjan(i); // 缩一波点
    }
    for1(i ,1 ,n)
    {
        for (int j = head[i]; j != -1; j = edge[j].next)
        {
            int v = edge[j].to;
            if ( belong[i] != belong[v] ) ind[belong[v]] ++;
        }
    }//统计当前缩完点后的每个点的入度
    sort(a + 1, a + 1 + n ,cmp1);
    for1(i ,1 ,n)
    {
        if (ind[belong[a[i].id]] == 0)
        {
            a[i].v = 0;
            ind[belong[a[i].id]] = 1;
        }
    }//删去一个联通块中权值最小的点
    sort(a + 1 , a + 1 + n ,cmp2);
    LL ans = 0, cnt = 0;
    for1(i ,1 ,n) //计算我们的答案
    {
        ans += a[i].v;
        cnt ++ ;
        if (cnt == k) break;
    }
    printf ("%lld\n", ans);
    return 0;
}