[笔记] 兰道定理 Landau's Theorem

兰道定理的内容：

一个竞赛图强连通的充要条件是：把它的所有顶点按照入度d从小到大排序，对于任意\(k\in [0,n-1]\)都不满足\(\sum_{i=0}^k d_i=\binom{k+1}{2}\)。

---

兰道定理的证明：

引理：

一个竞赛图强连通的充要条件是对于任意\(S \subsetneq 点集V\)，都存在一个点\(u \notin S\)，满足u到S有边。

证明：

1.必要性：比较显然

2.充分性：假设我们现在已经得到了\(V\)中的一个强连通子集\(S\)，想办法不断扩展\(S\)直到\(S=V\)。新建一个集合\(T\)，初始令\(T=S\)。我们选择集合T，根据引理中的条件，\(T\complement(T在V中的补集)\)中一定有至少一个点u到T有边。任意选择一个这样的点u，把他加入T，并且"标记"出u连到T的任意一条边。不断重复这样的过程，直到\(T=V\)。那么现在这张图会长成这样：

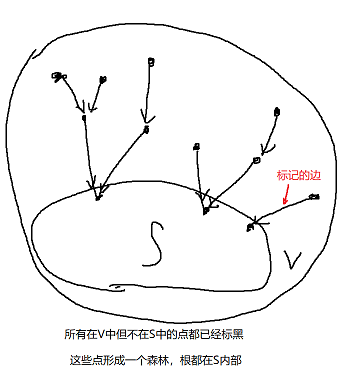
现在选择\(S\complement\)这个集合，根据引理条件S到它肯定有边，那么就会形成一条从S中出发，经过一些不属于S的点，再回到S的路径。路径上的点可以被加进S，这样就可以不断扩展S(类似耳分解)。

证明完这个引理之后就好办了，我们只需要判断\(V\)有没有"入度"为0的真子集即可。一个子集入度为零当且仅当子集内所有点的入度之和等于这个子集内部的边数，也就是\(\binom n2\)。到这里兰道定理就证完了。