WeetCode4 —— 二叉树遍历与树型DP

一丶二叉树的遍历

1.二叉树遍历递归写法与递归序

了解过二叉树的朋友，最开始肯定是从二叉树的遍历开始的，二叉树遍历的递归写法想必大家都有所了解。

public static void process(TreeNode node) {
    if (node == null) {
        return;
    }
    //如果在这里打印 代表前序遍历  ----位置1
    process(node.left);
    //如果在这里打印中序遍历       ----位置2
    process(node.right);
    //如果在这里打印 后序遍历      ---位置3
}

process函数在不同的位置进行打印，就实现了不同的遍历顺序。

我们这里引入一个概念递归序 —— 递归函数到达节点的顺序

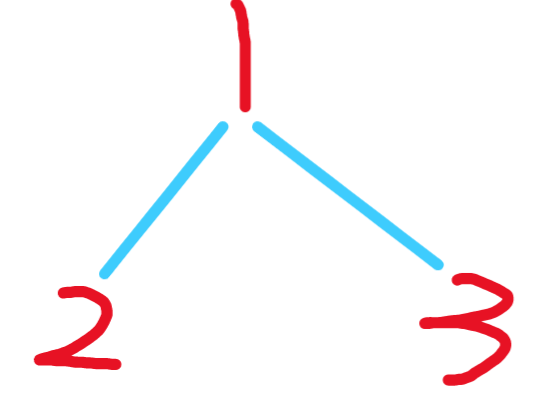
process函数的递归序列是什么呢

1. 首先process(1)此时方法栈记为A，遍历节点1（可以理解为A栈的位置1）
2. 然后process(1.left) 再开辟一个栈记为B 来到2（可以理解为B栈的位置1）
3. 接着process(2.left)为空 出栈 相当于来到了B栈的位置2 ，再次来到2
4. 接着process(2.right)为空，出栈，来到B栈位置3，再次来到2
5. 接着出栈，来到A栈位置2
6. 然后process(1.right)再开辟一个栈记为C 来到3（可以理解为C栈的位置1）
7. 接着process(3.left)为空 出栈 相当于来到了C栈的位置2 ，再次来到3
8. 接着process(3.right)为空，出栈，来到C栈位置3，再次来到3
9. 最后出栈，来到A栈的位置3，来到1

递归序为 1，2，2，2，1，3，3，3，1。可以看到每一个节点都将访问3次。

• 第一次访问的时候打印

  1,2,3 ——先序遍历

• 第二次访问的时候打印

  2,1,3——中序遍历

• 第三次访问的时候打印

  2,3,1 ——后序遍历

2.二叉树遍历非递归写法

下面讲解的二叉树遍历非递归写法，都针对下面这棵树

2.1 先序遍历

递归写法告诉我们，打印结果应该是1,2,4,5,3。

对于节点2，我们需要先打印2，然后处理4，然后处理5。栈先进后出，如果我们入栈顺序是4，5 那么会先打印5然后打印4，将无法实现先序遍历，所有我们需要先入5后入4。

• 当前打印的节点记忆为cur
• 打印
• cur的右节点（如果存在）入栈，然后左节点（如果存在）入栈
• 弹出栈顶进行处理，循环往复

程序如下

public static void process1(TreeNode root) {
    if (root == null) {
        return;
    }
    Stack<TreeNode> stackMemory = new Stack<>();
    stackMemory.push(root);
    while (!stackMemory.isEmpty()) {
        TreeNode temp = stackMemory.pop();
        System.out.println(temp.val);
        if (temp.right != null) {
            stackMemory.push(temp.right);
        }
        if (temp.left != null) {
            stackMemory.push(temp.left);
        }
    }
}

2.2 中序遍历

1. 将树的左边界放入栈中

   

   这时候栈中的内容是 （栈底）1->2->4（栈顶）

2. 然后弹出节点cur进行打印

   也就是打印4，如果cur具备右子树，那么将右子树的进行步骤一

3. 循环往复直到栈为空

为什么这可以实现左->中->右打印的中序遍历

首先假如当前节点是A，那么打印A的前提是，左子树打印完毕，在打印A的左子树的时候，我们会把A左子节点的右树入栈，这一保证了打印A之前，A的左子树被处理完毕，然后打印A

打印完A，如果A具备右子树，右子树会入栈，然后弹出，保证了打印完A后打印其右子树，从而实现左->中->右打印的中序遍历

public static void process2(TreeNode root) {
    if (root == null) {
        return;
    }
    Stack<TreeNode> stackMemory = new Stack<>();
    do {

        //首先左子树入栈
        //1
        while (root!=null){
            stackMemory.push(root);
            root = root.left;
        }

        //来到这儿，说明左子树都入栈了
        //弹出
        if (!stackMemory.isEmpty()){
            root = stackMemory.pop();
            System.out.println(root.val);

            //赋值为右子树，右子树会到1的代码位置，如果右子树，那么右子树会进行打印
            root = root.right;
        }
    }while (!stackMemory.isEmpty()||root!=null);
}

2.3 后序遍历

后续遍历就是左->右->头的顺序，那么只要我以头->左->右的顺序将节点放入收集栈中，最后从收集栈中弹出的顺序，就是左->右->头

public static void process3(TreeNode r) {
    if (r == null) {
        return;
    }
	//辅助栈
    Stack<TreeNode> help = new Stack<>();
	//收集栈
    Stack<TreeNode> collect = new Stack<>();

    help.push(r);
    while (!help.isEmpty()) {
        TreeNode temp = help.pop();
        collect.push(temp);
        if (temp.left != null) {
            help.push(temp.left);
        }
        if (temp.right != null) {
            help.push(temp.right);
        }
    }

    StringBuilder sb = new StringBuilder();
    while (!collect.isEmpty()) {
        sb.append(collect.pop().val).append(",");
    }
    System.out.println(sb);
}

3.二叉树宽度优先遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 （也是宽度优先遍历）即逐层地，从左到右访问所有节点）。

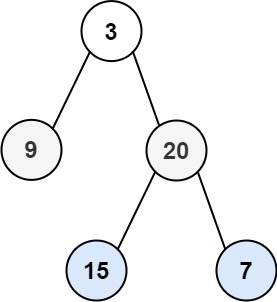
此树宽度优先遍历——[3],[9,20],[15,7]

宽度优先遍历可以使用队列实现，最开始将队列的头放入到队列中，然后当队列不为空的时候，拿出队列头cur，加入到结果集合中，然后如果当前cur的左儿子，右儿子中不为null的节点放入到队列中，循环往复

下面以LeetCode102为例子

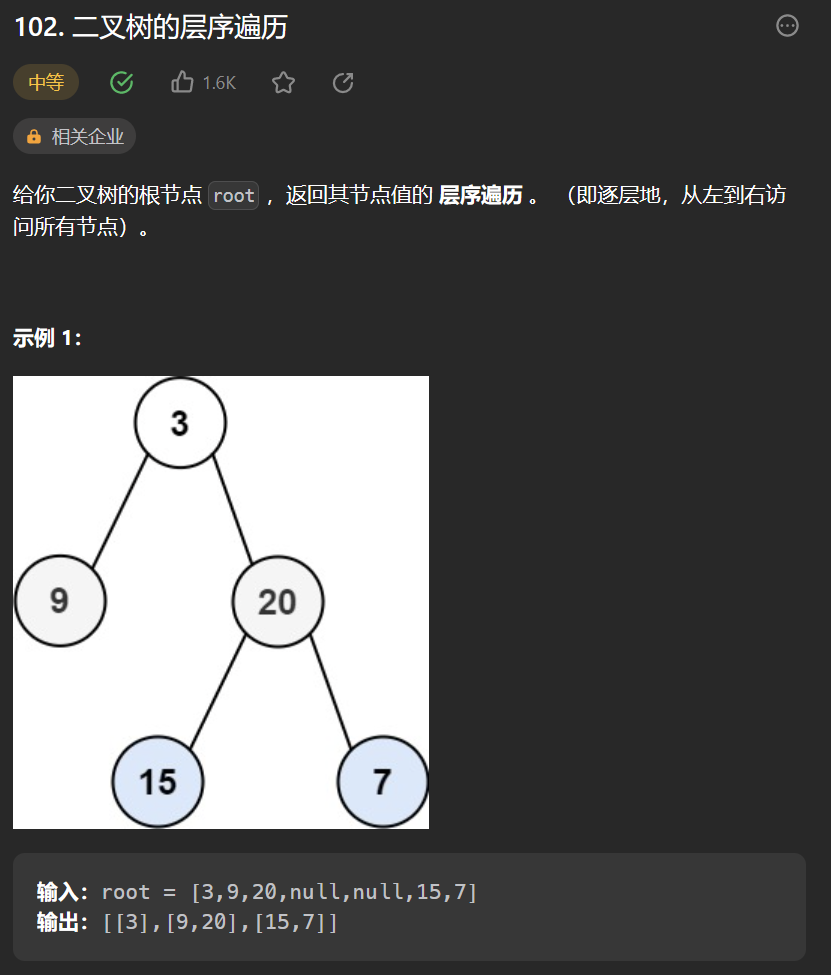
public List<List<Integer>> levelOrder(TreeNode root) {
    //结果集合
    List<List<Integer>> res = new ArrayList<>();
    if (root == null) {
        return res;
    }
    //队列
    LinkedList<TreeNode> queue = new LinkedList<>();
    queue.addLast(root);
    //当前层的节点数量为1
    int curLevelNum = 1;

    while (!queue.isEmpty()) {
        //存储当前层节点的值
        List<Integer> curLevelNodeValList = new ArrayList<>(curLevelNum);
        //下一层节点的数量
        int nextLevelNodeNum = 0;

        //遍历当前层
        while (curLevelNum > 0) {
            TreeNode temp = queue.removeFirst();
            curLevelNodeValList.add(temp.val);

            //处理左右儿子，只要不为null 那么加入并且下一次节点数量加1
            if (temp.left != null) {
                queue.addLast(temp.left);
                nextLevelNodeNum++;
            }
            if (temp.right != null) {
                queue.addLast(temp.right);
                nextLevelNodeNum++;
            }
            //当前层减少
            curLevelNum--;
        }
        //当前层结束了，到下一层
        curLevelNum = nextLevelNodeNum;
        //存储结果
        res.add(curLevelNodeValList);
    }
    return res;
}

二丶树型DP

1.从一道题开始——判断一颗二叉树是否是搜索二叉树

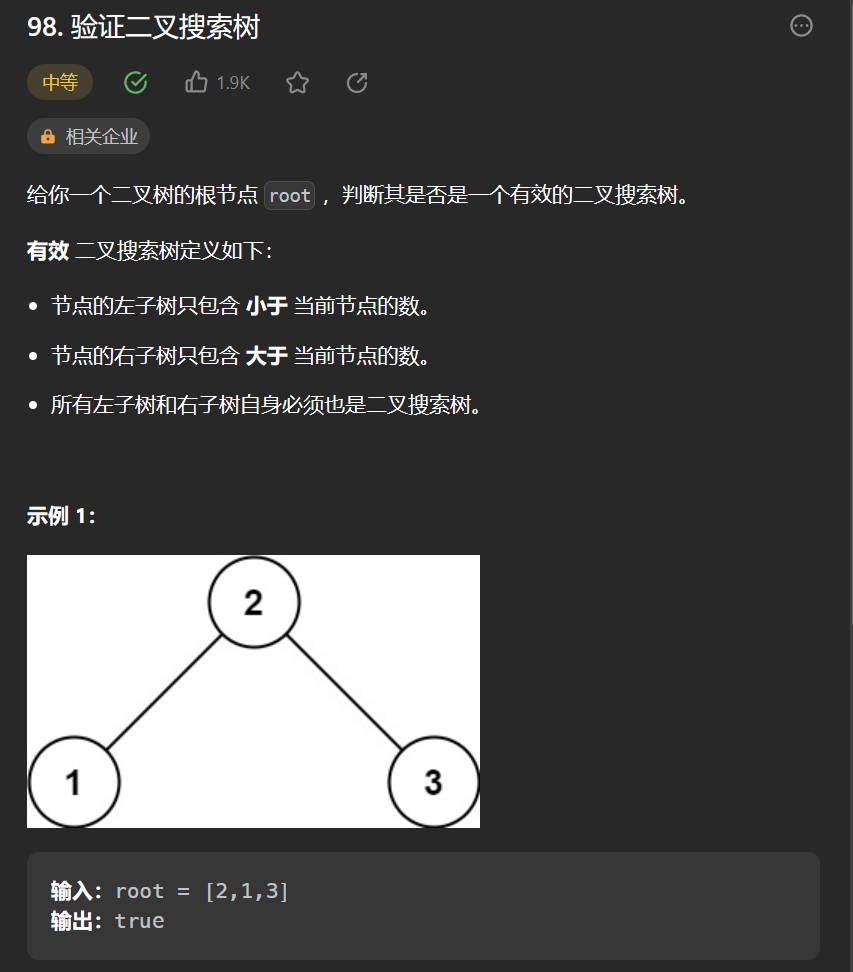
1.1 中序遍历解题

可以断定我们可以使用中序遍历，然后在中序遍历的途中判断节点的值是满足升序即可

• 递归中序遍历判断是否二叉搜索树

  public boolean isValidBST(TreeNode root) {
      if (root == null) {
          return true;
      }
  
      //第二个参数记录之前遍历遇到节点的最大值
      //由于TreeNode 可能节点值为int 最小使用Long最小
      return check(root, new AtomicLong(Long.MIN_VALUE));
  }
  
  private boolean check(TreeNode node, AtomicLong preValue) {
      if (node == null) {
          return true;
      }
  
      //左树是否二叉搜索树
      boolean isLeftBST = check(node.left, preValue);
  
      //左树不是 那么返回false
      if (!isLeftBST) {
          return false;
      }
      //当前节点的值 大于之前遇到的最大值 那么更改preValue
      if (node.val > preValue.get()) {
          preValue.set(node.val);
      } else {
          //不满足升序那么false
          return false;
      }
  
      //检查右树
      return check(node.right, preValue);
  }
  

• 非递归中序遍历判断是否二叉搜索树

  private boolean check(TreeNode root) {
      if (root == null) {
          return true;
      }
      //前面节点最大值，最开始为null
      Integer pre = null;
      Stack<TreeNode> stack = new Stack<>();
      do {
          while (root != null) {
              stack.push(root);
              root = root.left;
          }
          if (!stack.isEmpty()) {
              root = stack.pop();
  
              //满足升序那么更新pre
              if (pre == null || pre < root.val) {
                  pre = root.val;
              } else {
                  return false;
              }
              root = root.right;
          }
      } while (!stack.isEmpty() || root != null);
  
      return true;
  }
  

1.2 引入 —— 树形DP

如果当前位于root节点，我们可以获取root左子树的一些"信息"，root右子树的一些信息，我们们要如何判断root为根的树是否是二叉搜索树：

1. root左子树，右子树必须都是二叉搜索树

2. root的值必须大于左子树最大，必须小于右子树最小

3. 根据1和2 我们可以得到"信息"的结构

   static class Info {
   
       //当前子树的最小值
       Integer min;
       //当前子树最大值
       Integer max;
       //当前子树是否是二叉搜索树
       boolean isBst;
   
       Info(Integer min, Integer max, boolean flag) {
           this.min = min;
           this.max = max;
           this.isBst = flag;
       }
   }
   

接下来的问题是，有了左右子树的信息，如何拼凑root自己的信息？如果不满足二叉搜索树的要求那么返回isBst为false，否则需要返回root这棵树的最大，最小——这些信息可以根据左子树和右子树的信息构造而来。代码如下

private Info process(TreeNode node) {
    //如果当前节点为null 那么返回null
    //为null 表示是空树
    if (node == null) {
        return null;
    }

    //默认现在是二叉搜索树
    boolean isBst = true;

    //左树最大，右树最小 二者是否bst ，从左右子树拿信息
    Info leftInfo = process(node.left);
    Info rightInfo = process(node.right);
    //左树不为null 那么 维护isBst标识符
    if (leftInfo != null) {
        isBst = leftInfo.isBst;
    }
      //右树不为null 那么 维护isBst标识符
    if (rightInfo != null) {
        isBst = isBst && rightInfo.isBst;
    }

    //如果左数 或者右树 不为二叉搜索树 那么返回
    if (!isBst){
        return new Info(null,null,isBst);
    }
    //左右是bst，那么看是否满足二叉搜索树的条件

    //左边最大 是否小于当前节点
    if (leftInfo!=null && leftInfo.max >= node.val){
        isBst = false;
    }

    //右边最小 是否小于当前节点
    if (rightInfo!=null && rightInfo.min <= node.val){
        isBst = false;
    }

    //如果不满足 那么返回
    if (!isBst){
        return new Info(null,null,isBst);
    }
    //说明node为根的树是bst

    //那么根据左右子树的信息返回node这课树的信息
    Integer min  = node.val;
    Integer max  = node.val;
    if (leftInfo!=null){
        min = leftInfo.min;
    }
    if (rightInfo!=null){
        max = rightInfo.max;
    }
    return new Info(min, max, true);
}

2. 树型DP题目套路

之所以称之为树型DP，是因为这个套路用于解决 树的问题。那么为什么叫DP，这是由于node节点的信息，来自左右子树的信息，类似于动态规划中的状态转移。

2.1树型DP可以解决什么问题

怎么理解：

对于1中判断是否二叉搜索树的问题，S规则就是以node为根的这棵树是否是二叉搜索树

最终整棵树是否二叉搜索树，是依赖于树中所有节点的——"最终答案一定在其中"

2.2 解题模板

3.题目练习

3.1 二叉树的最大深度

需要的信息只有树的高度，我们可以向左子树获取，高度然后获取右子树的高度，然后二叉高度取max加上1就是当前节点为根的树的高度

  public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }

        int leftH = maxDepth(root.left);
        int rightH = maxDepth(root.right);

        return Math.max(leftH,rightH)+1;
    }

3.2 判断一颗树是否二叉平衡树

• 需要什么信息：左右树的高度，左右树是否是平衡的
• 怎么根据左右构造当前树的信息：当前高度=max（左右高度）+1 ，当前是否平衡=左平衡右平衡且二者高度差不大于1

/***
 * 是否是平衡二叉树
 * @return
 */
public static boolean isAVL(TreeNode root) {
    return process(root).getKey();
}

public static Pair<Boolean, Integer> process(TreeNode root) {
    //当前节点为null 那么是平衡二叉树
    if (root == null) {
        return new Pair<>(true, 0);
    }
    //右树
    Pair<Boolean, Integer> rightData = process(root.right);
    //左树
    Pair<Boolean, Integer> leftData = process(root.left);
    //右树是否是平衡
    boolean rTreeIsAVL = rightData.getKey();
    //右树高度
    int rHigh = rightData.getValue();
    //左树是否平衡
    boolean lTreeIsAVL = leftData.getKey();
    //左树高度
    int lHigh = rightData.getValue();
    //当前树是平衡要求：左树平衡 右树平衡 且二者高度差小于1
    boolean thisNodeIsAvl = rTreeIsAVL
            && lTreeIsAVL
            && Math.abs(rHigh - lHigh) < 2;
    //返回当前树的结果 高度树是左右高度最大+1
    return new Pair<>(thisNodeIsAvl, Math.max(rHigh, lHigh) + 1);
}

3.3 判断一棵树是否满二叉树

满二叉树 树的高度h和树节点数目n具备 n = 2的h次方 -1 的特性

• 需要左右树的高度，左右树的节点个数
• 怎么根据左右构造当前树的信息：当前高度=max（左高，右高）+1，当前节点个数=左个数+右个数+1

public static boolean isFullTree(TreeNode root) {
    Pair<Integer, Integer> rootRes = process(root);
    int height = rootRes.getKey();
    int nodeNums = rootRes.getValue();
    return nodeNums == Math.pow(2, height)-1;
}

//key 高度 v 节点个数
public static Pair<Integer, Integer> process(TreeNode node) {
    if (node == null) {
        return new Pair<>(0, 0);
    }
    Pair<Integer, Integer> rInfo = process(node.right);
    Pair<Integer, Integer> lInfo = process(node.left);
    int thisNodeHeight = Math.max(rInfo.getKey(), lInfo.getKey()) + 1;
    int thisNodeNum = rInfo.getValue() + lInfo.getValue() + 1;
    return new Pair<>(thisNodeHeight, thisNodeNum);
}