机器学习（十六）— LDA和PCA降维

一、LDA算法

　　基本思想：LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

　　浅显来讲，LDA方法的考虑是，对于一个多类别的分类问题，想要把它们映射到一个低维空间，如一维空间从而达到降维的目的，我们希望映射之后的数据间，两个类别之间“离得越远”，且类别内的数据点之间“离得越近”，这样两个类别就越好区分。因此LDA方法分别计算“within-class”的分散程度Sw和“between-class”的分散程度Sb，而我们希望的是Sb/Sw越大越好，从而找到最合适的映射向量w。

　　

　　LDA算法的主要优点有：

　　　　1）在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。

　　　　2）LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

　　LDA算法的主要缺点有：

　　　　1）LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。

　　　　2）LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。

　　　　3）LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。

　　　　4）LDA可能过度拟合数据。

二、PCA算法

1、基本思想：

　　主成分分析（Principal components analysis，以下简称PCA）是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。

　　PCA顾名思义，就是找出数据里最主要的方面，用数据里最主要的方面来代替原始数据。　

　　第一种解释是样本点到这个直线的距离足够近，第二种解释是样本点在这个直线上的投影能尽可能的分开。

　　我们知道“基于最小投影距离”就是样本点到这个超平面的距离足够近，也就是尽可能保留原数据的信息；而“基于最大投影方差”就是让样本点在这个超平面上的投影能尽可能的分开，也就是尽可能保留原数据之间的差异性。

　　假如我们把n'从1维推广到任意维，则我们的希望降维的标准为：样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。

　　基于上面的两种标准，我们可以得到PCA的两种等价推导。

2、优缺点

　　作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。

　　PCA算法的主要优点有：

　　　　1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。　

　　　　2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

　　　　3）计算方法简单，主要运算是特征值分解，易于实现。

　　　　4）当数据受到噪声影响时，最小的特征值所对应的特征向量往往与噪声有关，舍弃能在一定程度上起到降噪的效果。

　　　　PCA算法的主要缺点有：

　　　　1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

　　　　2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

　　为啥W'XX'W可以度量样本的差异性。最后得出结论：XX'就是X的协方差矩阵，其中对角线元素为各个字段的方差，而非对角线元素表示变量i和变量j两个字段的协方差。

　　注意：

　　由于 PCA 减小了特征维度，因而也有可能带来过拟合的问题。PCA 不是必须的，在机器学习中，一定谨记不要提前优化，只有当算法运行效率不尽如如人意时，再考虑使用 PCA 或者其他特征降维手段来提升训练速度。

　　降低特征维度不只能加速模型的训练速度，还能帮我们在低维空间分析数据，例如，一个在三维空间完成的聚类问题，我们可以通过 PCA 将特征降低到二维平面进行可视化分析。

3、算法流程

　　下面给出第一篇博文中总结的算法流程。

　　输入：n维样本集D=(x1,x2,...,xm)

　　输出：n'维样本集D'=(z1,z2,...,zm), 其中n'≤n

　　1. 对所有样本进行中心化（均值为0）：这是必须

　　

　　2. 计算样本的协方差矩阵XX'

　　3. 对协方差矩阵XX'进行特征分解（https://blog.csdn.net/jingyi130705008/article/details/78939463），得到对应的特征值和特征向量

　　4. 取出最大的n'个特征值对应的特征向量（w1,w2,...,wn'）,对其进行标准化，组成特征向量矩阵W

　　5. 对于训练集中的每一个样本，进行相应转换：

　　　

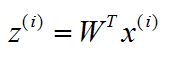
　　6. 得到输出样本集D'=(z1,z2,...,zm)

　　

　　备注：有时候，我们不指定降维后的n'的值，而是换种方式，指定一个降维到的主成分比重阈值t。这个阈值t在(0,1]之间。假如我们的n个特征值为λ1≥λ2≥...≥λn,则n'可以通过下式得到:

　　　　　　

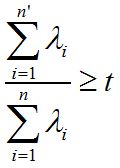
三、二者对比

　　LDA用于降维，和PCA有很多相同，也有很多不同的地方，因此值得好好的比较一下两者的降维异同点。

　　　　首先我们看看相同点：

　　　　1）两者均可以对数据进行降维。

　　　　2）两者在降维时均使用了矩阵特征分解的思想。

　　　　3）两者都假设数据符合高斯分布。

　　　　我们接着看看不同点：

　　　　1）LDA是有监督的降维方法，而PCA是无监督的降维方法

　　　　2）LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。

　　　　3）LDA除了可以用于降维，还可以用于分类。

　　　　4）LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。

参考文献：https://www.cnblogs.com/pinard/p/6244265.html