【bzoj2752】[HAOI2012]高速公路(road) 线段树

题目描述

Y901高速公路是一条重要的交通纽带，政府部门建设初期的投入以及使用期间的养护费用都不低，因此政府在这条高速公路上设立了许多收费站。
Y901高速公路是一条由N-1段路以及N个收费站组成的东西向的链，我们按照由西向东的顺序将收费站依次编号为1~N，从收费站i行驶到i+1(或从i+1行驶到i)需要收取Vi的费用。高速路刚建成时所有的路段都是免费的。
政府部门根据实际情况，会不定期地对连续路段的收费标准进行调整，根据政策涨价或降价。
无聊的小A同学总喜欢研究一些稀奇古怪的问题，他开车在这条高速路上行驶时想到了这样一个问题:对于给定的l,r(l<r),在第l个到第r个收费站里等概率随机取出两个不同的收费站a和b，那么从a行驶到b将期望花费多少费用呢?

输入

第一行2个正整数N,M，表示有N个收费站，M次调整或询问
接下来M行，每行将出现以下两种形式中的一种
C l r v 表示将第l个收费站到第r个收费站之间的所有道路的通行费全部增加v
Q l r   表示对于给定的l,r，要求回答小A的问题
所有C与Q操作中保证1<=l<r<=N

输出

对于每次询问操作回答一行，输出一个既约分数
若答案为整数a，输出a/1

样例输入

4 5
C 1 4 2
C 1 2 -1
Q 1 2
Q 2 4
Q 1 4

样例输出

1/1
8/3
17/6

---

题解

线段树

首先将每次修改和询问的r减1，把线段权值转化为点权值。

然后使用总和/总次数的方式计算期望。

考虑第$i$个点$(l\le i\le r)$，它被选中的次数为$(i-l+1)*(r-i+1)$，所以所求即为

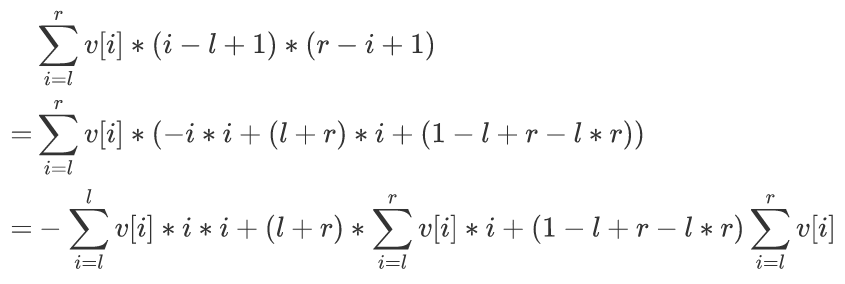
于是直接开3棵线段树维护$v[i]*i*i$、$v[i]*i$、$v[i]$的区间和即可。

注意要开long long。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 100010
#define lson l , mid , x << 1
#define rson mid + 1 , r , x << 1 | 1
using namespace std;
typedef long long ll;
struct data
{
    ll sum[N << 2] , si[N << 2] , add[N << 2];
    void pushdown(int x)
    {
        if(add[x])
        {
            sum[x << 1] += add[x] * si[x << 1] , add[x << 1] += add[x];
            sum[x << 1 | 1] += add[x] * si[x << 1 | 1] , add[x << 1 | 1] += add[x];
            add[x] = 0;
        }
    }
    void build(int flag , int l , int r , int x)
    {
        if(l == r)
        {
            if(flag == 0) si[x] = 1;
            else if(flag == 1) si[x] = l;
            else si[x] = (ll)l * l;
            return;
        }
        int mid = (l + r) >> 1;
        build(flag , lson) , build(flag , rson);
        si[x] = si[x << 1] + si[x << 1 | 1];
    }
    void update(int b , int e , ll a , int l , int r , int x)
    {
        if(b <= l && r <= e)
        {
            sum[x] += a * si[x] , add[x] += a;
            return;
        }
        pushdown(x);
        int mid = (l + r) >> 1;
        if(b <= mid) update(b , e , a , lson);
        if(e > mid) update(b , e , a , rson);
        sum[x] = sum[x << 1] + sum[x << 1 | 1];
    }
    ll query(int b , int e , int l , int r , int x)
    {
        if(b <= l && r <= e) return sum[x];
        pushdown(x);
        int mid = (l + r) >> 1;
        ll ans = 0;
        if(b <= mid) ans += query(b , e , lson);
        if(e > mid) ans += query(b , e , rson);
        return ans;
    }
}A , B , C;
char str[5];
ll gcd(ll a , ll b)
{
    return b ? gcd(b , a % b) : a;
}
int main()
{
    int n , m , x , y;
    ll z , t , d;
    scanf("%d%d" , &n , &m) , n -- ;
    A.build(0 , 1 , n , 1) , B.build(1 , 1 , n , 1) , C.build(2 , 1 , n , 1);
    while(m -- )
    {
        scanf("%s%d%d" , str , &x , &y) , y -- ;
        if(str[0] == 'C')
            scanf("%lld" , &z) , A.update(x , y , z , 1 , n , 1) , B.update(x , y , z , 1 , n , 1) , C.update(x , y , z , 1 , n , 1);
        else
        {
            t = (y - x + 1 - (ll)y * x) * A.query(x , y , 1 , n , 1) + (y + x) * B.query(x , y , 1 , n , 1) - C.query(x , y , 1 , n , 1);
            d = gcd(t , (ll)(y - x + 1) * (y - x + 2) / 2);
            printf("%lld/%lld\n" , t / d , (ll)(y - x + 1) * (y - x + 2) / 2 / d);
        }
    }
    return 0;
}