对A-Star寻路算法的粗略研究

首先来看看完成后的效果：

其中灰色代表路障，绿色是起点和移动路径，红色代表终点

// = openArray[i+1].F) {
minNode = openArray[i+1];
}
}
start = minNode;
//将新开始点加入关闭列表
close.push(start);

//将新开始点从开启列表中移除
for(i = 0; i ';
for(var j = -3; j '+j+','+i+'

';
} else {
html += ' '+j+','+i+'

';
}
}
html += '

';
}
t.innerHTML = html;
}

function addStone() {
var tdCollections = $('td');
for(var i = 0; i

为了继续学习，需要明白几个概念。

曼哈顿距离

曼哈顿距离的定义是，两个物体南北方向的距离与东西方向的距离之和。看起来就好像是直角三角形的两条边之和。

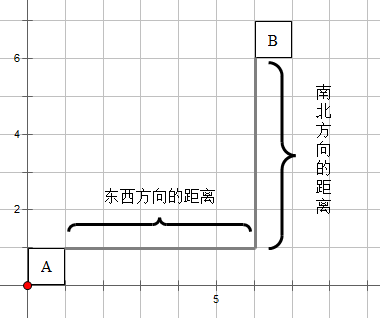
用代码表示出来就是：

/**

 * 计算两点间的曼哈顿距离

 * @param goalNode  {Object} 终点坐标

 * @param startNode {Object} 起点坐标

 * @returns {number} 两点间的曼哈顿距离

 */

function Manhattan(goalNode,startNode) {

    return Math.abs(goalNode.x - startNode.x) + Math.abs(goalNode.y - startNode.y);

}

公式F＝G+H

G：从起点开始，沿着计算出的可能路径，移动到该路径上的移动消耗。

H：计算出的可能路径到终点的移动预估消耗。

F：G与H之和。

以下图来说明：

起点S周围有四个可选路径a、b、c、d(为简单起见，不考虑对角线也可行走的情况)，先来看路径a。

从起点S到达a的移动耗费是1格，故G=1。而从a到达终点G的移动耗费估算是5格，故H=5。F是G与H的值相加，为6。

经过观察，a、b、c三个路径的F值是一样的。而d路径的F值为4。可见F值越小，到达终点的花费越少，因此应该选择d路径作为下一步。

到达d路径后，重复前面的过程，搜索周围的路径，找到F值最小的作为下一步，同时将这个路径作为新的起始点。因为接下来每个路径的F值

都是参照这个新起始点来计算的。

由上图可知，S通往G的最佳路径是d、e、f。

但是还有一种情况，比如下图(灰色表示路障，无法通行)：

e和f的F值是一样的，这时候选择哪个呢？其实都可以，一般选择最后一个被计算出来的路径即可。

具体实现

上述方法虽然可行，但是如果不加以限制，会造成一些不良后果。当从起点S到达新路径d时，d仍需要对周围的路径进行探索，起点S也将包含其中，很显然这是不必要而且浪费的。对此，我们需要维护两个列表，一个称为路径开启列表，一个称为路径关闭列表。

var open = [];  //开启列表

var close = [];  //关闭列表

open列表的职责是探索周围路径时，将可通行的路径(无路障的路径)加入列表中；

close列表则负责将各个新起点加入其中(相应的这些新起点也要从open列表中移除)，下一次执行路径探索时，如果该路径存在这个列表中，则忽略它。

当终点G被包含在close列表中时，搜索结束。

需要注意的是，为每个新起点标记它的父结点，即它是从哪里过来的(比如d路径的父结点就是S，e的父结点是d)，这样在到达终点G时，就能够根据它的父结点

一级一级地返回，从而找到这条“通路”的所有坐标，有点像链表这种数据结构。

完整代码：

html部分

<!doctype html>

<html lang="en">

<head>

    <meta charset="UTF-8">

    <title>a-star</title>

    <style>

        body{

            margin: 0;

            font-size:12px;

        }

        table{border-collapse: collapse;

            width: 100%; table-layout: fixed}

        table th,table td{border:1px solid #000}

        #t{

            width: 831px;

        }

        #t td{

            width: 30px;

            height: 30px;

            text-align: center;

        }

        .start{background-color: #00fc5f}

        .block{background-color:#cacaca}

        .goal{background-color: #ff2211}

        .visited{background-color: #009921;}

    </style>

    <script src="../jquery-2.1.3.js"></script>

</head>

<body>

<input id="start" type="button" value="开始寻路"/>

<script src="a-star.js"></script>

<script>

    $('#start').bind('click',function() {

        move(start,end);

    });

</script>

</body>

</html>

js部分

 var open = [],  //开启列表

     close = [], //关闭列表

     start = {}, //起点坐标

     end = {};   //终点坐标

 var d = document;

 /**

  * 检查待测坐标是否在坐标集合内

  * @param toBeCheckNode {Object} 待检查坐标 {x,y}

  * @param sourceNode {Array} 坐标集合

  * @returns {boolean} 待测坐标是否在坐标集合内

  */

 function isNodeExists(toBeCheckNode,sourceNode) {

     for(var i in sourceNode) {

         if (sourceNode.hasOwnProperty(i)) {

             if (parseInt(toBeCheckNode.x) === sourceNode[i].x && parseInt(toBeCheckNode.y) === sourceNode[i].y) return true;

         }

     }

     return false;

 }

 /**

  * 返回数组中的某个元素

  * @param el 待返回元素

  * @param arr 数组

  * @returns {Object} 返回该元素

  */

 function getElementInArray(el,arr) {

     for(var i in arr) {

         if(arr.hasOwnProperty(i)) {

             if(parseInt(el.x) === arr[i].x && parseInt(el.y) === arr[i].y) {

                 return arr[i];

             }

         }

     }

     return null;

 }

 /**

  * 计算两点间的曼哈顿距离

  * @param goalNode  {Object} 终点坐标

  * @param startNode {Object} 起点坐标

  * @returns {number} 两点间的曼哈顿距离

  */

 function Manhattan(goalNode,startNode) {

     return Math.abs(goalNode.x - startNode.x) + Math.abs(goalNode.y - startNode.y);

 }

 /**

  * 选择最佳路径作为新起始点

  * @param openArray {Array} 开启列表

  * @returns {Object} 返回新起始点

  */

 function selectNewStart(openArray) {

     var minNode = openArray[0],i;

     for(i = 0,len = openArray.length - 1; i < len; i++) {

         if(minNode.F >= openArray[i+1].F) {

             minNode = openArray[i+1];

         }

     }

     start = minNode;

     //将新开始点加入关闭列表

     close.push(start);

     //将新开始点从开启列表中移除

     for(i = 0; i < openArray.length; i++) {

         if(minNode.x === openArray[i].x && minNode.y === openArray[i].y) {

             openArray.splice(i,1);

             break;

         }

     }

     return start;

 }

 /**

  * 遍历周围节点并加入开启列表

  * @param node {Object} 一个起始点

  */

 function searchAround(node) {

     for(var i = -1; i <= 1;i++) {

         for(var j = -1; j <= 1; j++) {

             var x = node.x + i,

                 y = node.y + j;

             //判断是否为有效的路径点

             var nodeExsits = findCurrentPositionInfo(x,y) != null;

             if(!nodeExsits) continue;

             var t = parseInt(findCurrentPositionInfo(x,y).getAttribute('type'));

             if(!(x !== node.x && y !== node.y)) {

                 if(x!== node.x || y !== node.y) {

                     var curNode = {x:x,y:y,type:t};

                     //如果该坐标无法通行，则加入关闭列表中

                     if(curNode.type === 4 ||

                         curNode.type === 0 ||

                         curNode.type === 44) {

                         if(isNodeExists(curNode,close)) continue;

                         close.push(curNode);

                     }

                     //如果该坐标已在关闭列表中，略过

                     if(isNodeExists(curNode,close)) continue;

                     //如果该坐标已在开启列表中，则重新计算它的G值

                     if(isNodeExists(curNode,open)) {

                         var new_GValue = Manhattan(curNode,start),

                             //在开启列表中取出这个元素

                             inOpenNode = getElementInArray(curNode,open),

                             //取出旧的G值

                             old_GValue = inOpenNode.G;

                         //如果G值更小，则意味着当前到达它的路径比上一次的好，更新它的父结点

                         //以及G值，并重新计算它的F值

                         if(new_GValue < old_GValue) {

                             inOpenNode.parent = start;

                             inOpenNode.G = new_GValue;

                             inOpenNode.F = inOpenNode.G + inOpenNode.H;

                         }

                         continue;

                     }

                     //设置父节点

                     curNode.parent = {x:node.x,y:node.y};

                     curNode.G = Manhattan(curNode,node);

                     curNode.H = Manhattan(end,curNode);

                     //估算值

                     curNode.F = curNode.G + curNode.H;

                     //将坐标加入开启列表中

                     open.push(curNode);

                 }

             }

         }

     }

 }

 function findCurrentPositionInfo(x, y) {

     var tds = $('td'),

         s = x + "," + y;

     for(var i = 0; i < tds.length; i++) {

         if(tds[i].innerHTML === s) return tds[i];

     }

     return null;

 }

 function generateMap() {

     var t = d.createElement('table');

     t.id = 't';

     d.body.appendChild(t);

     var html = '';

     for(var i = -3; i < 10; i++) {

         html += '<tr>';

         for(var j = -3; j < 15; j++) {

             if(i === 0 && j === 0) {

                 html += '<td class="start" type="1">'+j+','+i+'</td>';

             } else {

                 html += '<td type="1">'+j+','+i+'</td>';

             }

         }

         html += '</tr>';

     }

     t.innerHTML = html;

 }

 function addStone() {

     for(var i = 0; i < 50; i++) {

         var r = Math.ceil(Math.random() * 233);

         if(r === 57) continue;

         var res = tdCollections.eq(r).addClass('block');

         res.attr('type',0);

     }

 }

 function setGoal() {

     var r = Math.ceil(Math.random() * 233);

     if(r === 57 || tdCollections.eq(r).hasClass('block')) return setGoal();

     var res = tdCollections.eq(r).addClass('goal');

     //var res = tdCollections.eq(24).addClass('goal');

     return {

         x:res.html().split(',')[0],

         y:res.html().split(',')[1]

     }

 }

 function setColor(start) {

     var x = start.x,

         y = start.y,

         el = findCurrentPositionInfo(x,y);

     $(el).addClass('visited');

 }

 function move(s,e) {

     searchAround(s);

     s = selectNewStart(open);

     setColor(s);

     if(!isNodeExists(e,close)) {

         setTimeout(function() {

             log();

             return move(s,e);

         },100);

     }

 }

 function init() {

     open = [];

     close = [];

     start = {};

     end = {};

 }

 function log() {

     console.log('当前起点：',start);

     console.log('开启列表：',open);

     console.log('关闭列表：',close);

 }

 generateMap();

 var tdCollections = $('td');

 addStone();

 end = setGoal();

 start = {x:0,y:0,type:1};

 close.push(start);

 //move(start,end);