Big Sur 11.0.1 让2K屏幕开启Hidpi

首先来个成果图：

一、复制显示器配置文件

---

终端输入命令：cd /System/Library/Displays/Contents/Resources/Overrides

接着输入：open .

打开DisplayVendorID-610文件夹找到DisplayProductID-a033，复制保存到桌面备用。

二、配置专属显示器文件

---

用FixEDID快速查看的外接显示器的2个数值，记下来

DisplayProductID

DisplayVendortID

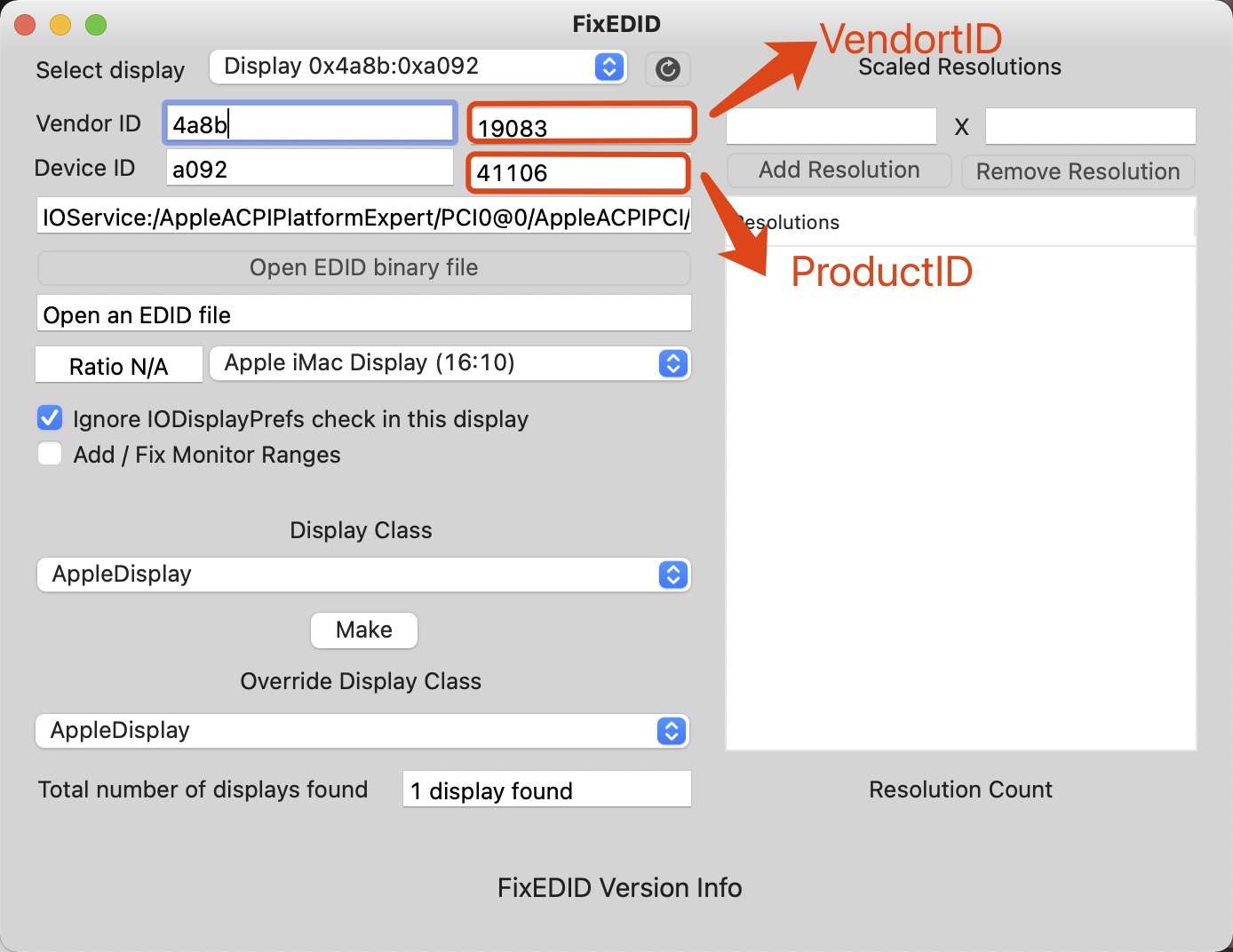
用PlistEdit Pro软件打开复制到桌面的DisplayProductID-a033

上图是成果，照这个改就行了，其他的都删掉。

第一个框框是DisplayProductID

第二个框框是DisplayVendortID

第三个框框是分辨率的16进制

PS：这里我自己保留0、1、2因为只用了三个分辨率，大家自己可以选择，删除多余的对象后，依次填你想要的HIDPI分辨率16进制的，比如1920×1080的HIDPI就要填入3840×2160的16进制00000F00 00000870 00

这三个分辨率分别是1920×1080,1600×900,1280×720对应的HIDPI的16进制分辨率。

三、关闭SIP(这玩意11.0.1真的有毒)

---

先声明我是黑苹果，我是直接在OC中修改的config.plist

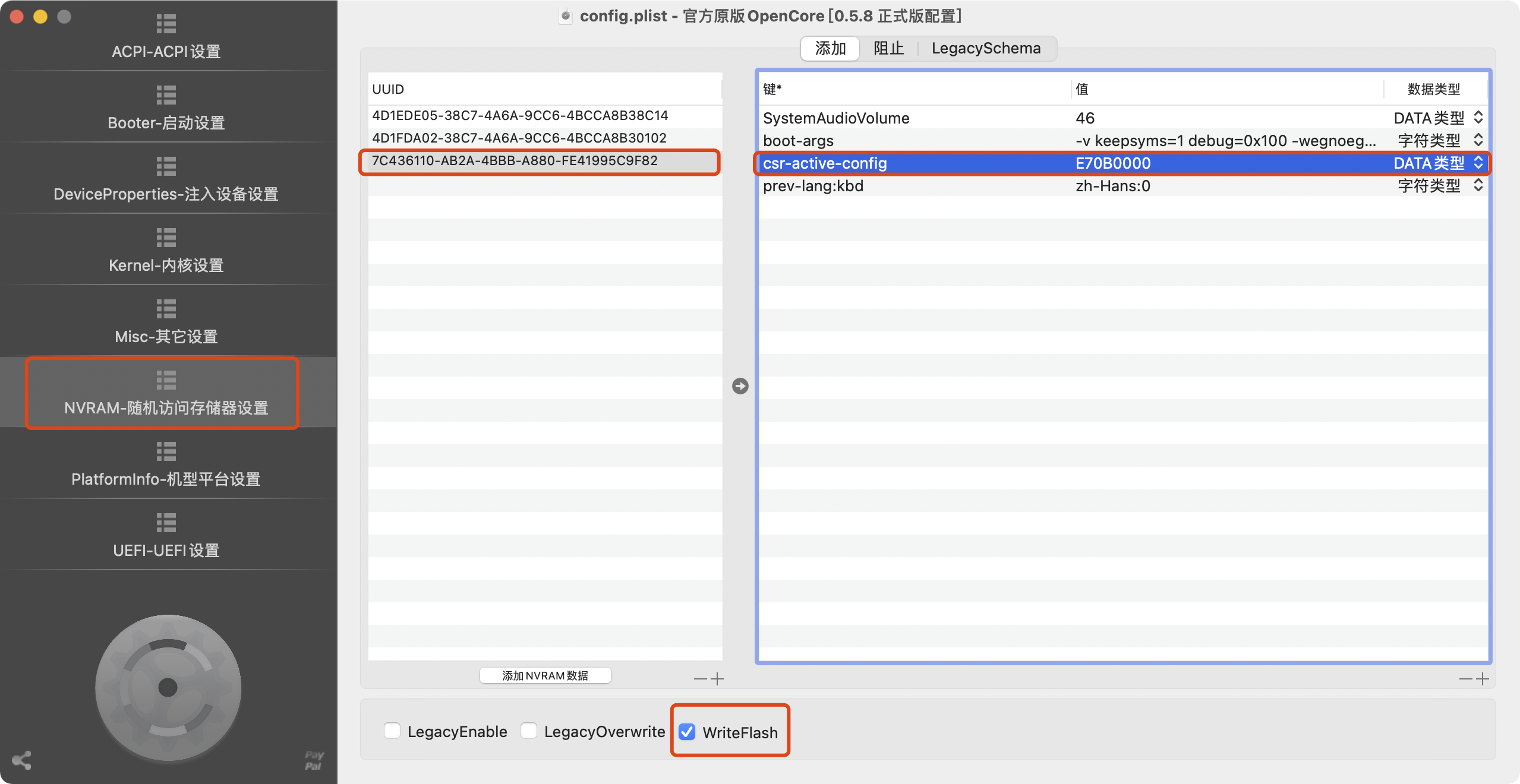
按照我选中的框框修改，csr-active-config 原本初始值是00000000，改成E70B0000即可关闭SIP

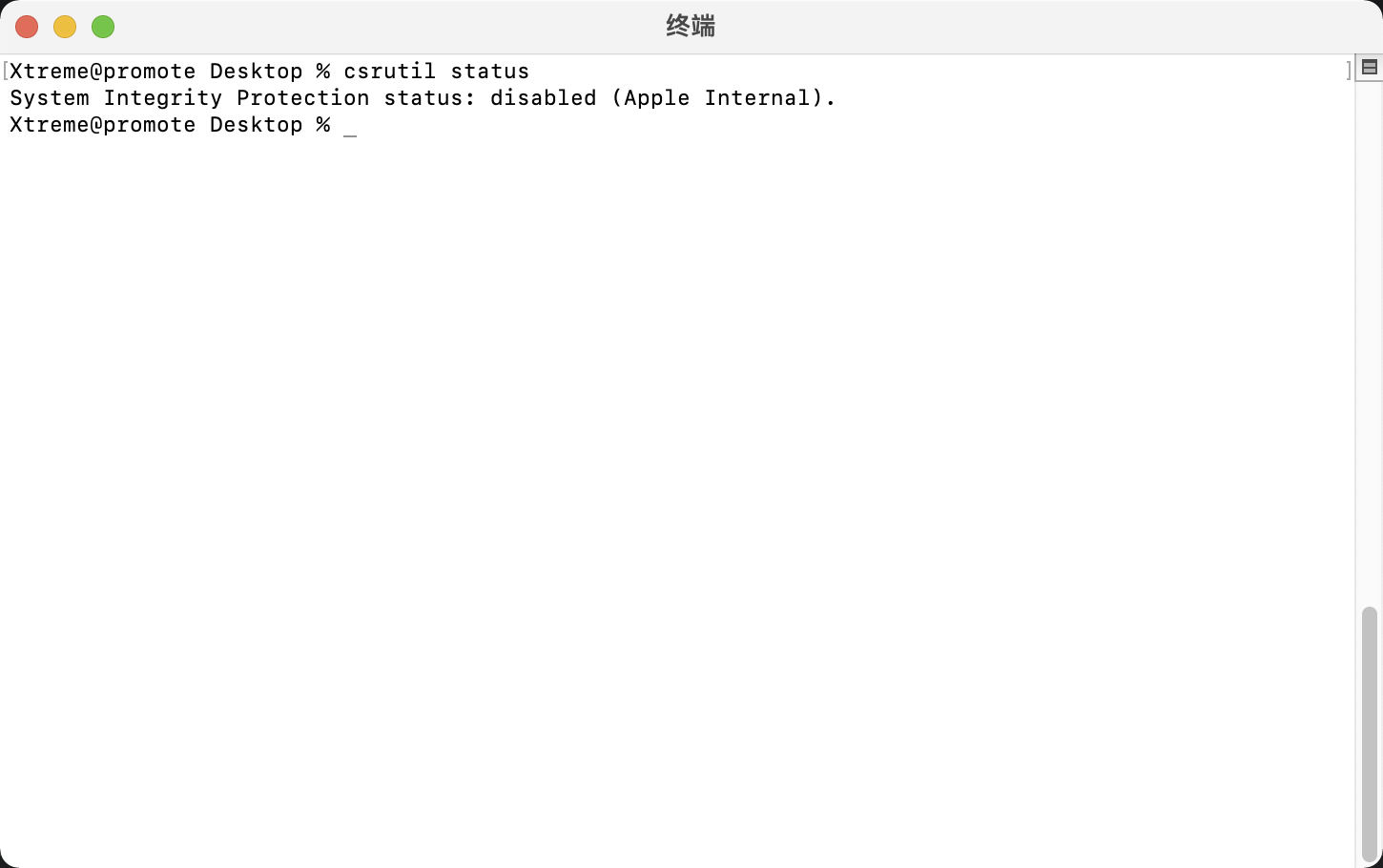
但是还没完... 重启系统

运行命令：csrutil status csrutil authenticated-root disable

看看有没有显示关闭

四、解决文件复制问题

---

将修改好的DisplayProductID-XXX文件放到DisplayVendorID-XXX文件夹里，然后整个文件夹复制到/System/Library/Displays/Contents/Resources/Overrides目录下

一句话的事，多简单呀~~~

但是他喵的复制文件一直提示没有权限，郁闷~~~

下面开始我的操作了

运行命令：diskutil list 查看MAC的系统盘是在哪里，注意是系统盘 不是数据盘

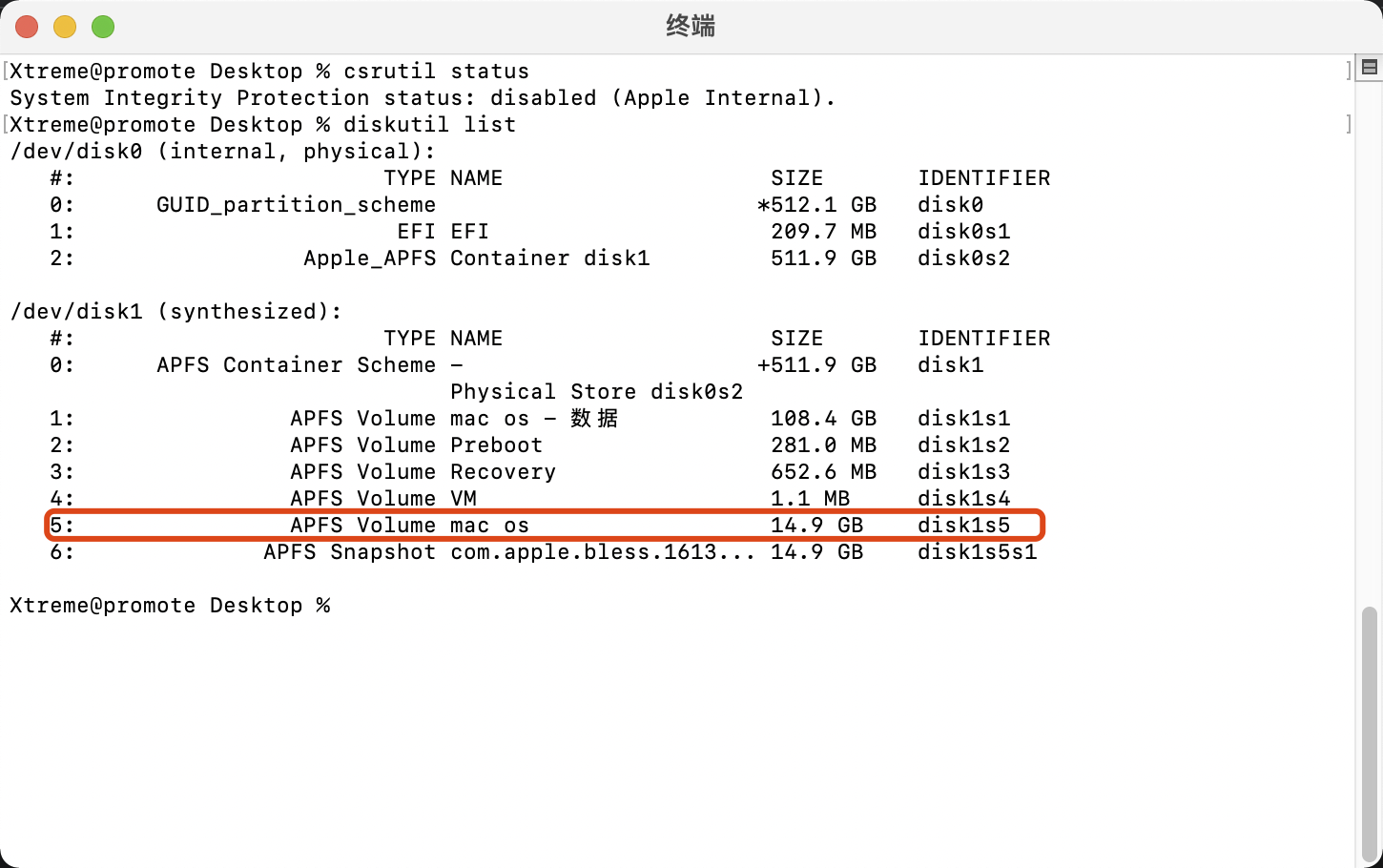
比如我的就是：disk1s5 把这个记下来

运行命令：sudo mount -o nobrowse -t apfs /dev/[磁盘名] [挂载路径]

解释下：[磁盘名] = disk1s5 [挂载路径] = /Users/你的用户名/随便某个目录

比如我运行命令：sudo mount -o nobrowse -t apfs /dev/disk1s5 /Users/Xtreme/Downloads

接下来复制文件，可以用Finder直接拖进去，或者用命令：sudo cp -R [配置文件路径] [挂载路径]/System/Library/Displays/Contents/Resources/Overrides

PS：复制完就重启，第一次启动logo会变大，之后就没事了。