强化学习 3—— 使用蒙特卡洛采样法（MC）解决无模型预测与控制问题

一、问题引入

回顾上篇强化学习 2 —— 用动态规划求解 MDP我们使用策略迭代和价值迭代来求解MDP问题

1、策略迭代过程：

1、评估价值 (Evaluate)

\[v_{i}(s) = \sum_{a\in A} \pi(a|s) \left( {\color{red}R(s, a)} + \gamma \sum_{s' \in S} {\color{red}P(s'|s, a)} \cdot v_{i-1}(s') \right)
\]

2、改进策略（Improve）

\[q_i(s,a) = {\color{red}R(s, a)} + \gamma \sum_{s' \in S} {\color{red}P_{(s'|s,a)}} \cdot v_i(s') \\
\pi_{i+1}(s) = argmax_a \; q^{\pi_i}(s,a)
\]

2、价值迭代过程：

\[v_{i+1}(s) \leftarrow max_{a \in A} \; \left({\color{red}R(s, a)} + \gamma \sum_{s' \in S} {\color{red}P_{(s'|s,a)}} \cdot V_i(s')\right)
\]

然后提取最优策略 $ \pi $

\[\pi^*(s) \leftarrow argmax_a \; \left({\color{red}R(s, a)} + \gamma \sum_{s' \in S} {\color{red}P_{(s'|s,a)}} \cdot V_{end}(s')\right)
\]

可以发现，对于这两个算法，有一个前提条件是奖励 R 和状态转移矩阵 P 我们是知道的，因此我们可以使用策略迭代和价值迭代算法。对于这种情况我们叫做 Model base。同理可知，如果我们不知道环境中的奖励和状态转移矩阵，我们叫做 Model free。

不过有很多强化学习问题，我们没有办法事先得到模型状态转化概率矩阵 P，这时如果仍然需要我们求解强化学习问题，那么这就是不基于模型（Model Free）的强化学习问题了。

其实稍作思考，大部分的环境都是属于 Model Free 类型的，比如熟悉的雅达利游戏等等。另外动态规划还有一个问题：需要在每一次回溯更新某一个状态的价值时，回溯到该状态的所有可能的后续状态。导致对于复杂问题计算量很大。

所以，我们本次探讨在 Model Free 情况下的策略评估方法，策略控制部分留到下篇讨论。对于 Model Free 类型的强化学习模型如下如所示：

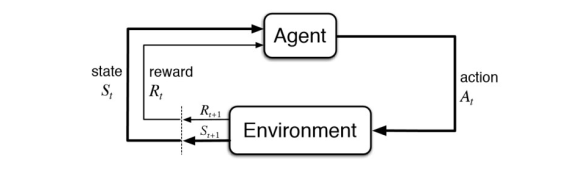
此时需要智能体直接和环境进行交互，环境根据智能体的动作返回下一个状态和相应的奖励给智能体。这时候就需要智能体搜集和环境交互的轨迹（Trajectory / episode）。

对于 Model Free 情况下的策略评估，我们介绍两种采样方法。蒙特卡洛采样法（Monte Carlo）和时序差分法（Temporal Difference）

二、蒙特卡洛采样法（MC）

对于Model Free 我们不知道奖励 R 和状态转移矩阵，那应该怎么办呢？很自然的，我们就想到，让智能体和环境多次交互，我们通过这种方法获取大量的轨迹信息，然后根据这些轨迹信息来估计真实的 R 和 P。这就是蒙特卡洛采样的思想。

蒙特卡罗法通过采样若干经历完整的状态序列(Trajectory / episode)来估计状态的真实价值。所谓的经历完整，就是这个序列必须是达到终点的。比如下棋问题分出输赢，驾车问题成功到达终点或者失败。有了很多组这样经历完整的状态序列，我们就可以来近似的估计状态价值，进而求解预测和控制问题了。

1、MC 解决预测问题

一个给定策略 $\pi$ 的完整有 T 个状态的状态序列如下

\[\{S_1, A_1, R_1, S_2, A_2, R_2, \cdots,S_T, A_T, R_T\}
\]

在马尔科夫决策（MDP）过程中，我们对价值函数 $v_\pi(s)$ 的定义:

\[v_\pi(s) = E_\pi[G_t|S_t = s] = E_\pi[R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3} | S_t = s]
\]

可以看出每个状态的价值函数等于所有该状态收获的期望，同时这个收获是通过后续的奖励与对应的衰减乘积求和得到。那么对于蒙特卡罗法来说，如果要求某一个状态的状态价值，只需要求出所有的完整序列中该状态出现时候的收获再取平均值即可近似求解，也就是：

\[G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3}+\cdots \gamma^{T-t-1}R_T
\]

\[v_\pi(s) \approx average(G_t) \quad s.t.\; S_t = s
\]

上面预测问题的求解公式里，我们有一个average的公式，意味着要保存所有该状态的收获值之和最后取平均。这样浪费了太多的存储空间。一个较好的方法是在迭代计算收获均值，即每次保存上一轮迭代得到的收获均值与次数，当计算得到当前轮的收获时，即可计算当前轮收获均值和次数。可以通过下面的公式理解：

\[\mu_t = \frac{1}{t}\sum_{j=1}^tx_j = \frac{1}{t}\left( x_t + \sum_{j=1}^{t-1}x_j \right) = \frac{1}{t}\left( x_t + (t-1)\mu_{t-1} \right) \\
\Downarrow \\
\mu_t = = \mu_{t-1} + \frac{1}{t}(x_t-\mu_{t-1})
\]

这样上面的状态价值公式就可以改写成：

\[N(S_t) \leftarrow N(S_t) + 1 \\
v(S_t) \leftarrow v(S_t) + \frac{1}{N(S_t)}(G_t-v(S_t))
\]

这样我们无论数据量是多还是少，算法需要的内存基本是固定的。我们可以把上面式子中 $\frac{1}{N(S_t)}$ 看做一个超参数 $\alpha$ ，可以代表学习率。

\[v(S_t) \leftarrow v(S_t) + \alpha(G_t-v(S_t))
\]

对于动作价值函数$Q(S_t, A_t)$，类似的有：

\[Q(S_t, A_t) = Q(S_t, A_t) + \alpha(G_t - Q(S_t, A_t))
\]

2、MC 解决控制问题

MC 求解控制问题的思路和动态规划策略迭代思路类似。在动态规划策略迭代算法中，每轮迭代先做策略评估，计算出价值 $v_k(s)$ ，然后根据一定的方法（比如贪心法）更新当前策略 $\pi$ 。最后得到最优价值函数 $v_*$ 和最优策略$\pi_*$ 。在文章开始处有公式，还请自行查看。

对于蒙特卡洛算法策略评估时一般时优化的动作价值函数 $q_*$，而不是状态价值函数 $v_*$ 。所以评估方法是：

\[Q(S_t, A_t) = Q(S_t, A_t) + \alpha(G_t - Q(S_t, A_t))
\]

蒙特卡洛还有一个不同是一般采用$\epsilon - 贪婪法$更新。$\epsilon -贪婪法$通过设置一个较小的 $\epsilon$ 值，使用 $1-\epsilon$ 的概率贪婪的选择目前认为有最大行为价值的行为，而 $\epsilon$ 的概率随机的从所有 m 个可选行为中选择，具体公式如下：

\[\pi(a|s) =
\begin{cases}
\epsilon/|A| + 1 - \epsilon, & \text{if $a^* = argmax_a \; q(s,a)$} \\
\epsilon/|A|, & \text{otherwise}
\end{cases}
\]

在实际求解控制问题时，为了使算法可以收敛，一般 $\epsilon$ 会随着算法的迭代过程逐渐减小，并趋于0。这样在迭代前期，我们鼓励探索，而在后期，由于我们有了足够的探索量，开始趋于保守，以贪婪为主，使算法可以稳定收敛。

Monte Carlo with $\epsilon - Greedy$ Exploration 算法如下：

3、在策略评估问题中 MC 和 DP 的不同

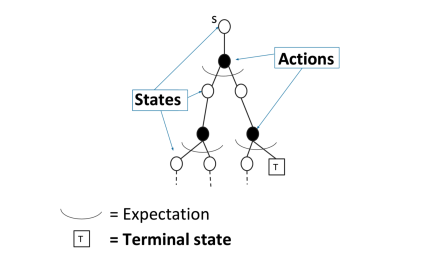
对于动态规划（DP）求解

通过 bootstrapping上个时刻次评估的价值函数 $v_{i-1}$ 来求解当前时刻的价值函数 $v_i$ 。通过贝尔曼等式来实现：

\[V_{t+1}(s) = \sum_{a \in A}\pi(a|s) \left(R(s, a) + \gamma \sum_{s' \in S} P_{(s'|s, a)} \cdot V_t(s')\right)
\]

对于蒙特卡洛（MC）采样

MC通过一个采样轨迹来更新平均价值

\[v(S_t) \leftarrow v(S_t) + \alpha(G_t-v(S_t))
\]

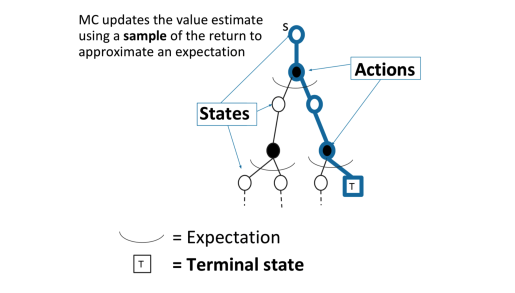
MC可以避免动态规划求解过于复杂，同时还可以不事先知道奖励和装填转移矩阵，因此可以用于海量数据和复杂模型。但是它也有自己的缺点，这就是它每次采样都需要一个完整的状态序列。如果我们没有完整的状态序列，或者很难拿到较多的完整的状态序列，这时候蒙特卡罗法就不太好用了。如何解决这个问题呢，就是下节要讲的时序差分法（TD）。

如果觉得文章写的不错，还请各位看官老爷点赞收藏加关注啊，小弟再此谢谢啦

参考资料：

B 站周老师的强化学习纲要第三节上