集训作业 洛谷P1443 马的遍历

这个题是个搜索，而且有是最少的步数，肯定就是广搜啦，不知道为什么的同学先去学习一下广搜吧。

养成好习惯，看见最少步数就去想想广搜（只是我自己觉得）

竟然这个题可以如此顺畅的想到广搜，感觉不难啊，但还有一个奇怪的地方，

emm，这个有点冷门啊，没事，讲讲（百度一下）就知道了。

奉上百度答案：printf("%-5d",x);

这句话的意思就是左对齐，宽5格，输出x。

到这里我们几乎就全讲完了（我讲的好水，听不的懂的同学去隔壁dgdger的博客看看吧，传送门）

广搜嘛，我直接附上之前讲广搜的链接吧，广搜。

对了，还有一个马的走法，我直接上图吧

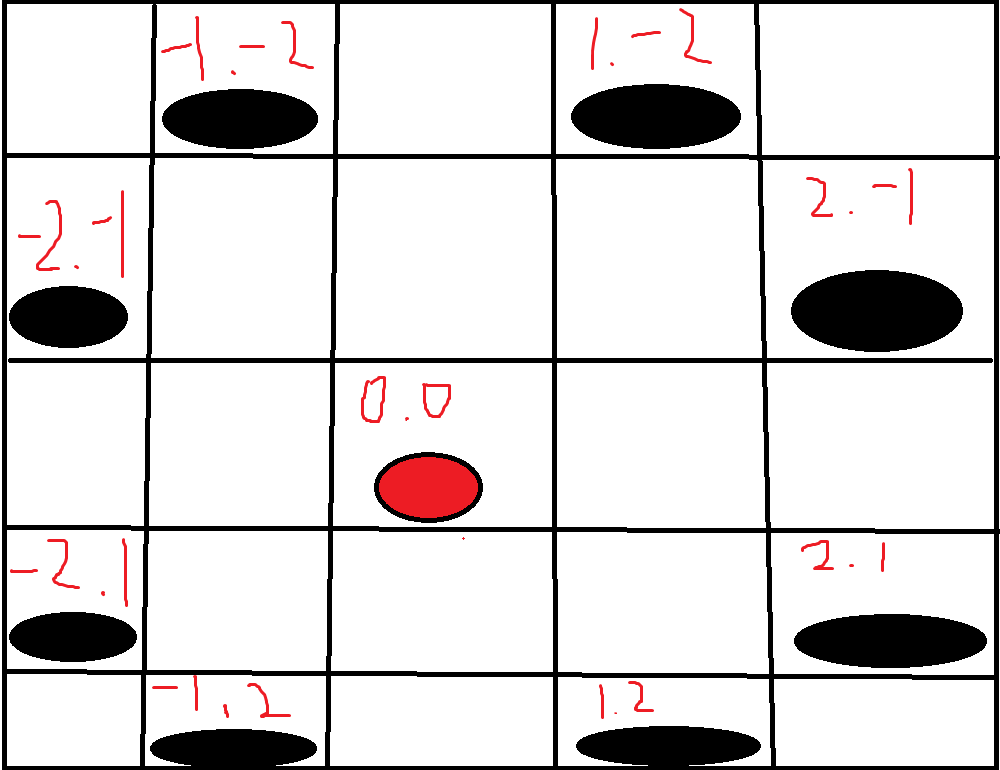
红色的实心圆是马的位置，剩下的黑实心圆是可以走到的位置，上面的红字是坐标（应该是对的）

emm，接下来的讲解就打成注释吧，要仔细看代码哦。

#include<iostream>
#include<cstdio>
using namespace std;
struct z
{
	int x,y,bushu=0;
}ma[200000];//400*400=160000
int a1[10]={1,-1,1,-1,-2,-2,2,2};//这是控制马移动方向的数组，a1是x，a2是y
int a2[10]={-2,-2,2,2,-1,1,-1,1};//众所周知，马走日，所以就这样写了。
int a[500][500],book[500][500],n,m,qx,qy,zx,zy,t,w;//a是记录到达每个点最小位置的数组，book就是记忆化数组。
int main()
{
	cin>>n>>m>>qx>>qy;//正常的输入
	a[qx][qy]=-1;//来一波初始化，为什么要初始化成-1呢？因为这样不被走到的地方就直接是-1了，不用另外判断。
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			a[i][j]=-1;
		}
	}
	a[qx][qy]=0;//出生点不需要走就可以到达。
	book[qx][qy]=1;//来过出生点，再来就是绕路了。
	t=0;//头和尾
	w=0;
	ma[t].x=qx;//这里我用的数组，queue也可以的。
	ma[t].y=qy;//存下位置
	ma[t].bushu=0;//存下步数
	t++;
	while(w<t)//还是有地方可以走的（目前不绕路的地方）
	{
		for(int i=0;i<8;i++)//马有8个走法
		{
			zx=ma[w].x+a1[i];//zx和zy表示这一次走完后的位置。
			zy=ma[w].y+a2[i];
			if(zx<=n&&zx>0&&zy<=m&&zy>0&&book[zx][zy]==0)//如果没有绕圈子，也没有越界，才可以储存
			{
				//绕圈子就是广搜中的记忆化搜索，大家可以学一下
				book[zx][zy]=1;//现在我来过这个地方了。下次来就可以知道是绕圈子了。
				ma[t].x=zx;//存下来
				ma[t].y=zy;
				ma[t].bushu=ma[w].bushu+1;//我从上一个地方走来，用ma[w].bushu步，走到这里用了一步，加起来就是从起点走到这里用的步数啦。
				a[zx][zy]=ma[t].bushu;//这个位置是第一次来，那就一定是最小步数。
				t++;
			}
		}
		w++;//别忘了w++，重复查看一个点是会TLE的。
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
            printf("%-5d",a[i][j]);//左对齐，宽5格
		}
		cout<<endl;
	}
	return 0;//完美结束
}

这个题和别的广搜没啥区别，如果你这个题过不了，希望你去学习或巩固一下广搜。

结束了……