SAP ABAP RFC接口通用日志工具：abap fm logger

很早之前就想写个能记录函数模块日志的通用工具，最早尝试时，没有想清楚插入代码的体积问题。在一些群友的提醒下，了解到可以用宏来处理这一问题。不过当时比较忙，就没有动笔。最近又想起这件事，花了2天完成了一个初步的实现。介绍给大家，希望能有参考价值。

本文链接：https://www.cnblogs.com/hhelibeb/p/13560754.html

简介

目标

本工具有几个目标：

把日志数据存储到一个统一日志表中，避免为每个接口创建日志表，从而减少重复工作量。
用一段通用代码实现日志存储，可以通过配置表来开关功能。
以JSON格式存储日志，并提供一定的索引查询功能。
允许根据日志的唯一ID来重处理数据（类似WE19）。

目前目标1, 2已经实现，3, 4部分实现，还有进一步完善的空间。

原理

基本原理是使用一些动态编程技术，在函数运行时获取参数值，转换为JSON数据存储到表中。

日志使用唯一ID作为主键。

重处理时，根据日志记录，动态生成ABAP变量，并从JSON中获取值，赋值给变量，再动态地调用日志中记录的FM。

代码量目前还很比较少，只有几百行，可以阅读包含文件ZAFL_MACROS和类ZCL_AFL_UTILITIES以了解更多细节。

关于ABAP动态编程，如果有不懂的地方，可以参考：这一系列文章：Dynamic Programming in ABAP

项目地址

项目名：abap fm logger

Github地址：https://github.com/hhelibeb/abap-fm-logger

请使用ABAPGIT安装，如果你觉得有帮助的话，欢迎Star.

使用

介绍abap fm logger的用法，包含代码、配置、报表等。

报表

日志存储在表ZAFL_LOG中，报表程序ZAFL_VIEWER可以用于查询/重处理日志

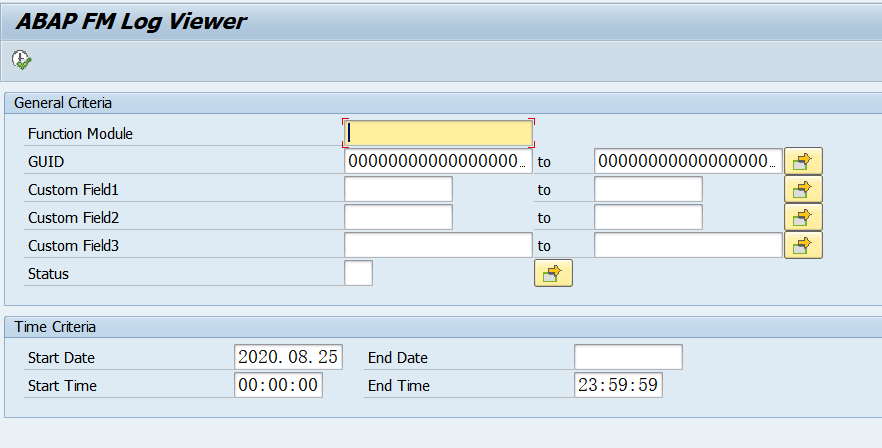
点击JSON字段可以查看参数详情。

选中日志行，点击工具栏的“Process Selected Item”，则程序会尝试使用选中的日志的参数记录重新调用相应接口。

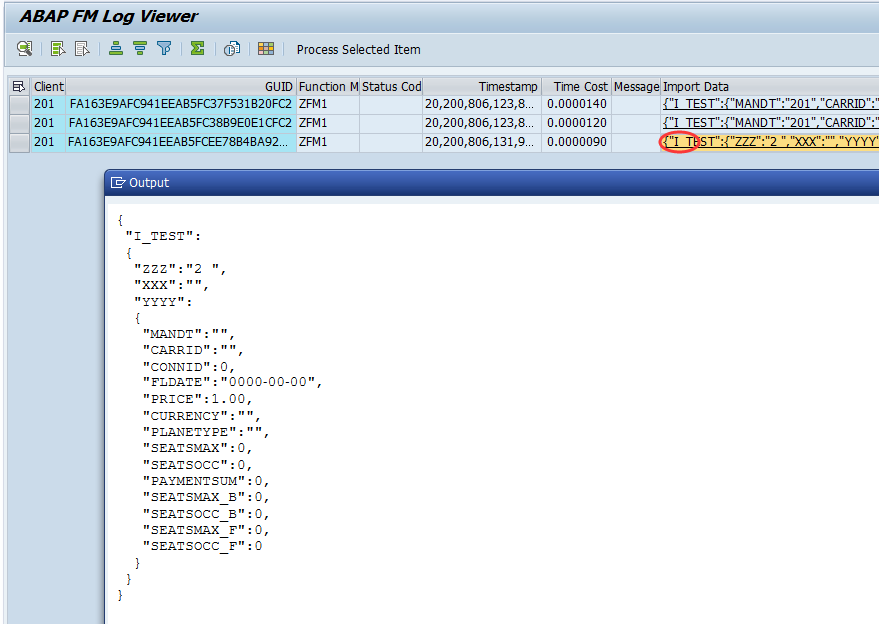
日志存储

只需要2个复制粘贴就能完成代码部分，非常简单：

1, 添加包含文件ZAFL_MACROS到需要记录日志的FM的函数组中，

FUNCTION-POOL zzxxxx.
INCLUDE zafl_macros.

2, 在函数中调用相应的宏，

FUNCTION z_fm.
 
**初始化logger，需要在FM的开头部分调用
  /afl/log_init.
 
**可选，最多指定3个用于搜索的字段（比如公司代码、物料号等）
  /afl/set_custom_fields 'cust field1' 'cust field2' 'cust field3'. 
 
**可选，记录状态码，如S/E等，最多2位
  /afl/set_status 'S' 'message'.
 
**保存日志，必须在FM的结尾处
  /afl/save.
 
ENDFUNCTION.

这里， /afl/log_init 和 /afl/save 是必选的，而 /afl/set_custom_fields 和 /afl/set_status 提供了一些灵活功能，可以按需选择是否调用。

配置

表ZAFL_CONFIG用于配置abap fm logger的功能，选项包括，

FNAME: 函数模块名。
ENABLED: 如勾选，启用日志记录功能。
EXPORT: 如勾选，启用Export参数的记录。
IMPORT: 如勾选，启用IMPORT参数的记录。

另外还可以指定3个索引字段的显示名（CUST_NAME），它们会影响的ZAFL_VIEWER中的显示效果。
可以使用事务SM30维护配置。

待改进

目前发现有2个问题需要改进，

如果接口包含CURR类型字段，虽然可以正常记录日志，但重处理时会无法读取日志中的CURR类型字段值。
没有按字段值搜索日志的功能（类似WE10）。

希望近期可以改进。

（注：严格来说它应该叫做函数模块接口通用日志工具，标题中的RFC是为了搜索关键字考虑的，因此这个工具的正式名称也叫做abap fm logger）