interp1

vq = interp1(x,v,xq) 使用线性插值返回一维函数在特定查询点的插入值。向量 x 包含样本点，v 包含对应值 v(x)。向量 xq 包含查询点的坐标。

如果您有多个在同一点坐标采样的数据集，则可以将 v 以数组的形式进行传递。数组 v 的每一列都包含一组不同的一维样本值。

vq = interp1(x,v,xq,method) 指定备选插值方法：'linear'、'nearest'、'next'、'previous'、'pchip'、'cubic'、'v5cubic'、'makima' 或 'spline'。默认方法为 'linear'。

vq = interp1(x,v,xq,method,extrapolation) 用于指定外插策略，来计算落在 x 域范围外的点。如果希望使用 method 算法进行外插，可将 extrapolation 设置为 'extrap'。您也可以指定一个标量值，这种情况下，interp1 将为所有落在 x 域范围外的点返回该标量值。

vq = interp1(v,xq) 返回插入的值，并假定一个样本点坐标默认集。默认点是从 1 到 n 的数字序列，其中 n 取决于 v 的形状：

当 v 是向量时，默认点是 1:length(v)。
当 v 是数组时，默认点是 1:size(v,1)。

如果您不在意点之间的绝对距离，则可使用此语法。

vq = interp1(v,xq,method) 指定备选插值方法中的任意一种，并使用默认样本点。

vq = interp1(v,xq,method,extrapolation) 指定外插策略，并使用默认样本点。

pp = interp1(x,v,method,'pp') 使用 method 算法返回分段多项式形式的 v(x)。

注意

不建议使用该语法。请改用 griddedInterpolant。

示例

基于粗略采样的正弦函数进行插值

定义样本点 x 及其对应样本值 v。

x = 0:pi/4:2*pi;

v = sin(x);

将查询点定义为 x 范围内更精细的采样点。

xq = 0:pi/16:2*pi;

在查询点插入函数并绘制结果。

figure

vq1 = interp1(x,v,xq);

plot(x,v,'o',xq,vq1,':.');

xlim([0 2*pi]);

title('(Default) Linear Interpolation');

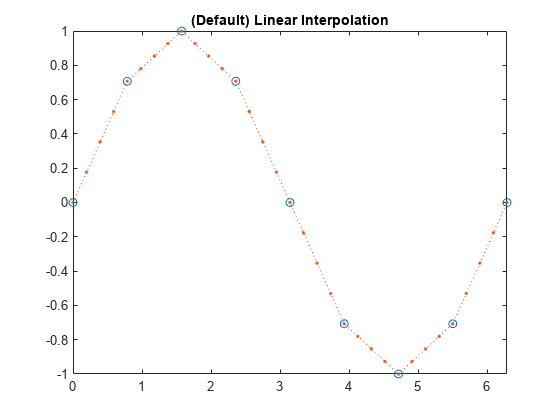
现在使用 'spline' 方法计算相同点处的 v。

figure

vq2 = interp1(x,v,xq,'spline');

plot(x,v,'o',xq,vq2,':.');

xlim([0 2*pi]);

title('Spline Interpolation');

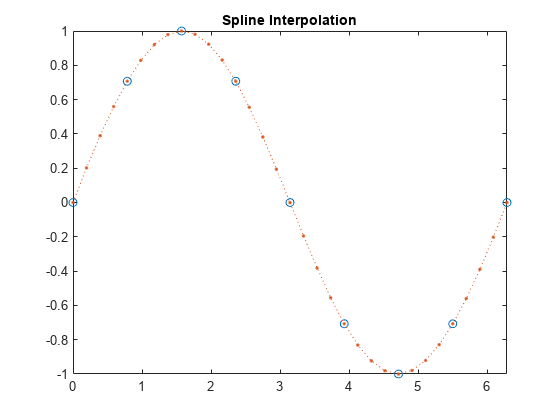
在不指定样本点的情况下进行插值

定义一组函数值。

v = [0  1.41  2  1.41  0  -1.41  -2  -1.41 0];

定义一组介于默认点 1:9 之间的查询点。在这种情况下，默认点为 1:9，因为 v 包含 9 个值。

xq = 1.5:8.5;

计算 xq 处的 v。

vq = interp1(v,xq);

绘制结果。

figure

plot((1:9),v,'o',xq,vq,'*');

legend('v','vq');

复数值插值

定义一组样本点。

x = 1:10;

定义函数 v(x)=5x+x2i 在样本点处的值。

v = (5*x)+(x.^2*1i);

将查询点定义为 x 范围内更精细的采样点。

xq = 1:0.25:10;

在查询点处进行 v 插值。

vq = interp1(x,v,xq);

用红色绘制结果的实部，用蓝色绘制虚部。

figure

plot(x,real(v),'*r',xq,real(vq),'-r');

hold on

plot(x,imag(v),'*b',xq,imag(vq),'-b');

日期和时间的插值

对时间戳数据点进行插值。

以包含温度读数的数据集为例，这些读数每四个小时测量一次。创建包含一天的数据的表，并绘制数据图。

x = (datetime(2016,1,1):hours(4):datetime(2016,1,2))';

x.Format = 'MMM dd, HH:mm';

T = [31 25 24 41 43 33 31]';

WeatherData = table(x,T,'VariableNames',{'Time','Temperature'})

WeatherData=7×2 table

        Time         Temperature

    _____________    ___________

    Jan 01, 00:00        31

    Jan 01, 04:00        25

    Jan 01, 08:00        24

    Jan 01, 12:00        41

    Jan 01, 16:00        43

    Jan 01, 20:00        33

    Jan 02, 00:00        31

plot(WeatherData.Time, WeatherData.Temperature, 'o')

插入数据集以预测一天中每一分钟内的温度读数。由于数据是周期性的，因此请使用 'spline' 插值方法。

xq = (datetime(2016,1,1):minutes(1):datetime(2016,1,2))';

V = interp1(WeatherData.Time, WeatherData.Temperature, xq, 'spline');

绘制插入的点。

hold on

plot(xq,V,'r')

使用两种不同方法进行外插

定义样本点 x 及其对应样本值 v。

x = [1 2 3 4 5];

v = [12 16 31 10 6];

指定查询点 xq，这些查询点延伸到 x 的定义域以外。

xq = [0 0.5 1.5 5.5 6];

使用 'pchip' 方法计算 xq 处的 v。

vq1 = interp1(x,v,xq,'pchip')

vq1 = 1×5

   19.3684   13.6316   13.2105    7.4800   12.5600

接着，使用 'linear' 方法计算 xq 处的 v。

vq2 = interp1(x,v,xq,'linear')

vq2 = 1×5

   NaN   NaN    14   NaN   NaN

现在将 'linear' 方法与 'extrap' 选项结合使用。

vq3 = interp1(x,v,xq,'linear','extrap')

vq3 = 1×5

     8    10    14     4     2

'pchip' 默认外插，但 'linear' 不会。

为 x 域范围外的所有查询指定常量值

定义样本点 x 及其对应样本值 v。

x = [-3 -2 -1 0 1 2 3];

v = 3*x.^2;

指定查询点 xq，这些查询点延伸到 x 的定义域以外。

xq = [-4 -2.5 -0.5 0.5 2.5 4];

现在使用 'pchip' 方法计算 xq 处的 v，并为 x 域范围外的所有查询点赋予值 27。

vq = interp1(x,v,xq,'pchip',27)

vq = 1×6

   27.0000   18.6562    0.9375    0.9375   18.6562   27.0000

在一个传递点插入多组数据

定义样本点。

x = (-5:5)';

在 x 所定义的点处对三个不同的抛物线函数采样。

v1 = x.^2;

v2 = 2*x.^2 + 2;

v3 = 3*x.^2 + 4;

创建矩阵 v，其列为向量 v1、v2 和 v3。

v = [v1 v2 v3];

将一组查询点 xq 定义为 x 范围内更精细的采样点。

xq = -5:0.1:5;

计算 xq 处的全部三个函数，并绘制结果。

vq = interp1(x,v,xq,'pchip');

figure

plot(x,v,'o',xq,vq);

h = gca;

h.XTick = -5:5;

绘图中的圆圈表示 v，实线表示 vq。

输入参数

`x` - 样本点
向量

样本点，指定为一行或一列实数向量。x 中的值必须各不相同。x 的长度必须符合以下要求之一：

如果 v 为向量，则 length(x) 必须等于 length(v)。
如果 v 为数组，则 length(x) 必须等于 size(v,1)。

示例： [1 2 3 4 5 6 7 8 9 10]

示例： 1:10

示例： [3 7 11 15 19 23 27 31]'

数据类型： single | double | duration | datetime

`v` - 样本值
向量 | 矩阵 | 数组

样本值，指定为实数/复数向量、矩阵或数组。如果 v 是矩阵或数组，则每列包含单独的一组一维值。

如果 v 包含复数，则 interp1 将分别插入实部和虚部。

示例： rand(1,10)

示例： rand(10,1)

示例： rand(10,3)

数据类型： single | double | duration | datetime
复数支持：是

`xq` - 查询点
标量 | 向量 | 矩阵 | 数组

查询点，指定为实数标量、向量、矩阵或数组。

示例： 5

示例： 1:0.05:10

示例： (1:0.05:10)'

示例： [0 1 2 7.5 10]

数据类型： single | double | duration | datetime

`method` - 插值方法
`'linear'` （默认） | `'nearest'` | `'next'` | `'previous'` | `'pchip'` | `'cubic'` | `'v5cubic'` | `'makima'` | `'spline'`

插值方法，指定为下表中的选项之一。

方法	说明	连续性	注释
`'linear'`	线性插值。在查询点插入的值基于各维中邻点网格点处数值的线性插值。这是默认插值方法。	C0	需要至少 2 个点。比最近邻点插值需要更多内存和计算时间。
`'nearest'`	最近邻点插值。在查询点插入的值是距样本网格点最近的值。	不连续	需要至少 2 个点。最低内存要求最快计算时间
`'next'`	下一个邻点插值。在查询点插入的值是下一个抽样网格点的值。	不连续	需要至少 2 个点。内存要求和计算时间与 `'nearest'` 相同
`'previous'`	上一个邻点插值。在查询点插入的值是上一个抽样网格点的值。	不连续	需要至少 2 个点。内存要求和计算时间与 `'nearest'` 相同
`'pchip'`	保形分段三次插值。在查询点插入的值基于邻点网格点处数值的保形分段三次插值。	C1	需要至少 4 个点。比 `'linear'` 需要更多内存和计算时间
`'cubic'` 注意 `interp1(...,'cubic')` 的行为在以后的版本中会有所变化。在以后的版本中，此方法将执行三次卷积。	与 `'pchip'` 相同。	C1	此方法目前返回与 `'pchip'` 相同的结果。
`'v5cubic'`	用于 MATLAB 5 的三次卷积。	C1	点之间的间距必须均匀。`'cubic'` 将在以后的版本中替代 `'v5cubic'`。
`'makima'`	修正 Akima 三次 Hermite 插值。在查询点插入的值基于次数最大为 3 的多项式的分段函数。为防过冲，已修正 Akima 公式。	C1	需要至少 2 个点。产生的波动比 `'spline'` 小，但不像 `'pchip'` 那样急剧变平计算成本高于 `'pchip'`，但通常低于 `'spline'` 内存要求与 `'spline'` 类似
`'spline'`	使用非结终止条件的样条插值。在查询点插入的值基于各维中邻点网格点处数值的三次插值。	C2	需要至少 4 个点。比 `'pchip'` 需要更多内存和计算时间

`extrapolation` - 外插策略
`'extrap'` | 标量值

外插策略，指定为 'extrap' 或实数标量值。

如果希望 interp1 使用与内插所用相同的方法来计算落在域范围外的点，则指定 'extrap'。
如果希望 interp1 为落在域范围外的点返回一个特定常量值，则指定一个标量值。

默认行为取决于输入参数：

如果您指定 'pchip'、'spline' 或 'makima' 插值方法，则默认行为是 'extrap'。
任何其他方法都会为落在域范围外的查询点默认返回 NaN。

示例： 'extrap'

示例： 5

数据类型： char | string | single | double

输出参数

`vq` - 插入的值
标量 | 向量 | 矩阵 | 数组

插入的值，以标量、向量、矩阵或数组的形式返回。vq 的大小取决于 v 和 xq 的形状。

v 的形状	xq 的形状	Vq 的大小	示例
向量	向量	`size(xq)`	如果 `size(v) = [1 100]` 且 `size(xq) = [1 500]`，则 `size(vq) = [1 500]`。
向量	矩阵或 N 维数组	`size(xq)`	如果 `size(v) = [1 100]` 且 `size(xq) = [50 30]`，则 `size(vq) = [50 30]`。
矩阵或 N 维数组	向量	`[length(xq) size(v,2),...,size(v,n)]`	如果 `size(v) = [100 3]` 且 `size(xq) = [1 500]`，则 `size(vq) = [500 3]`。
矩阵或 N 维数组	矩阵或 N 维数组	`[size(xq,1),...,size(xq,n),... size(v,2),...,size(v,m)]`	如果 `size(v) = [4 5 6]` 且 `size(xq) = [2 3 7]`，则 `size(vq) = [2 3 7 5 6]`。

`pp` - 分段多项式
结构体

分段多项式，以可传递到 ppval 函数进行计算的结构体的形式返回。

详细信息