洛谷P3355 骑士共存问题

题目描述

在一个 n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

　　

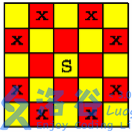
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

输入输出格式

输入格式：

第一行有 2 个正整数n 和 m (1<=n<=200, 0<=m<n2)，分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 2 个正整数，表示障碍的方格坐标。

输出格式：

将计算出的共存骑士数输出

输入输出样例

输入样例#1： 复制

3 2
1 1
3 3

输出样例#1： 复制

5 

最大流与最小割之间的转换

最多放多少骑士==最少拿走多少

观察图片不难发现：黄色的不能攻击黄色的，红色同理

那么不难想到二分图匹配

这样就转化成了二分图最小定点覆盖

而二分图最小顶点覆盖==二分图最大匹配。证明可以看[这里](http://www.cnblogs.com/jianglangcaijin/p/6035945.html)

从S向红色连边（权重为1），从红色向能攻击到的黄色连边（权重为INF），从黄色向T连边（权重为1）

 

// luogu-judger-enable-o2
#include<cstdio>
#include<cstring>
#include<queue>
#define AddEdge(x,y,z) add_edge(x,y,z),add_edge(y,x,0);
using namespace std;
const int MAXN=,INF=1e8+;
inline char nc()
{
    static char buf[MAXN],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,,MAXN,stdin),p1==p2)?EOF:*p1++;
}
inline int read()
{
    char c=nc();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=nc();}
    while(c>=''&&c<=''){x=x*+c-'';c=nc();}
    return x*f;
}
int N,M,S,T;
struct node
{
    int u,v,flow,nxt;
}edge[MAXN*];
int head[MAXN],cur[MAXN],num=;
inline void add_edge(int x,int y,int z)
{
    edge[num].u=x;
    edge[num].v=y;
    edge[num].flow=z;
    edge[num].nxt=head[x];
    head[x]=num++;
}
int deep[MAXN];
inline bool BFS()
{
    memset(deep,,sizeof(deep));
    deep[S]=;
    queue<int>q;
    q.push(S);
    while(q.size()!=)
    {
        int p=q.front();
        q.pop();
        for(int i=head[p];i!=-;i=edge[i].nxt)
            if(!deep[edge[i].v]&&edge[i].flow)
            {
                deep[edge[i].v]=deep[p]+;q.push(edge[i].v);
                if(edge[i].v==T) return ;
            }
    }
    return deep[T];
}
int DFS(int now,int nowflow)
{
    if(now==T||nowflow<=)    return nowflow;
    int totflow=;
    for(int &i=cur[now];i!=-;i=edge[i].nxt)
    {
        if(deep[edge[i].v]==deep[now]+&&edge[i].flow)
        {
            int canflow=DFS(edge[i].v,min(nowflow,edge[i].flow));
            edge[i].flow-=canflow;edge[i^].flow+=canflow;
            totflow+=canflow;
            nowflow-=canflow;
            if(nowflow<=) break;
        }
    }
    return totflow;
}
int Dinic()
{
    int ans=;
    while(BFS())
    {
        memcpy(cur,head,sizeof(head));
        ans+=DFS(S,INF);
    }
    return ans;
}
int a[][],c[][];
int xx[]={,-,-,-,-,+,+,+,+};
int yy[]={,-,-,+,+,+,+,-,-};
int main()
{
    #ifdef WIN32
    freopen("a.in","r",stdin);
    #else
    #endif
    memset(head,-,sizeof(head));
    N=read();M=read();S=;T=N*N+;
    for(int i=;i<=M;i++)
    {
        int x=read(),y=read();
        c[x][y]=;
    }
    for(int i=;i<=N;i++)
        for(int j=;j<=N;j++)
            a[i][j]=(i-)*N+j;
    for(int i=;i<=N;i++)
        for(int j=;j<=N;j++)
        {
            if(c[i][j]) continue;
            if((i+j)%)
            {
                AddEdge(S,a[i][j],);
                for(int k=;k<=;k++)
                {
                    int wx=i+xx[k],wy=j+yy[k];
                    if(wx>=&&wx<=N&&wy>=&&wy<=N)
                        AddEdge(a[i][j],a[wx][wy],INF);
                }
            }
            else AddEdge(a[i][j],T,);
        }
    printf("%d",N*N-M-Dinic());

    return  ;
}