POJ——T2446 Chessboard

http://poj.org/problem?id=2446

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 18560		Accepted: 5857

Description

Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below). 

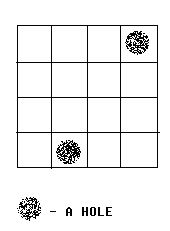
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below: 
1. Any normal grid should be covered with exactly one card. 
2. One card should cover exactly 2 normal adjacent grids.

Some examples are given in the figures below: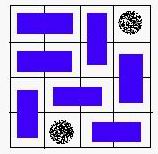 
 
A VALID solution.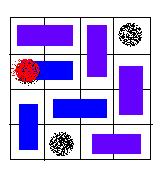
 
An invalid solution, because the hole of red color is covered with a card.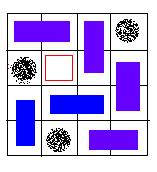
 
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

Input

There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.

Output

If the board can be covered, output "YES". Otherwise, output "NO".

Sample Input

4 3 2
2 1
3 3

Sample Output

YES

Hint

 
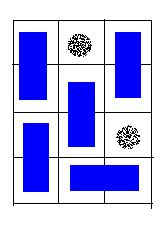
A possible solution for the sample input.

Source

POJ Monthly,charlescpp

 

题解：

把棋盘染成这个样子，有障碍的不染，用黑色格子与白色格子匹配，对这一个二分图求最大匹配。如果Ans*2+K=N*M,则能完全覆盖

 #include <algorithm>
 #include <cstring>
 #include <cstdio>

 using namespace std;

 const int N(*);
 int n,m,p,x,y,ans;
 int match[N][N][],lose[N][N];
 int vis[N][N],sumvis;
 int fx[]={,,-,};
 int fy[]={,,,-};

 bool DFS(int x,int y)
 {
     for(int i=;i<;i++)
     {
         int xx=x+fx[i], yy=y+fy[i];
         if(vis[xx][yy]!=sumvis&&!lose[xx][yy])
         {
             vis[xx][yy]=sumvis;
             if(!match[xx][yy][]||DFS(match[xx][yy][],match[xx][yy][]))
             {
                 match[xx][yy][]=x;
                 match[xx][yy][]=y;
                 return true;
             }
         }
     }
     return false;
 }

 int main()
 {
     while(~scanf("%d%d%d",&n,&m,&p))
     {
         if((n*m-p)%)
         {
             printf("NO\n");
             continue;
         }
         ans=sumvis=;
         memset(vis,,sizeof(vis));
         memset(lose,,sizeof(lose));
         memset(match,,sizeof(match));
         for(int i=;i<=p;i++)
         {
             scanf("%d%d",&x,&y);
             lose[y][x]=;
         }
         for(int i=;i<=n;i++)
             lose[i][]=lose[i][m+]=;
         for(int i=;i<=m;i++)
             lose[][i]=lose[n+][i]=;
         for(int i=;i<=n;i++)
           for(int j=;j<=m;j++)
             if((i+j)%==&&!lose[i][j])
             {
                 sumvis++;
                 if(DFS(i,j)) ans++;
             }
         if(ans*+p==m*n) printf("YES\n");
         else printf("NO\n");
     }
     return ;
 }