Codeforces 651 C. Watchmen-曼哈顿距离和欧几里得距离

C. Watchmen

 

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Watchmen are in a danger and Doctor Manhattan together with his friend Daniel Dreiberg should warn them as soon as possible. There are n watchmen on a plane, the i-th watchman is located at point (x_i, y_i).

They need to arrange a plan, but there are some difficulties on their way. As you know, Doctor Manhattan considers the distance between watchmen i and j to be |x_i - x_j| + |y_i - y_j|. Daniel, as an ordinary person, calculates the distance using the formula .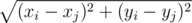

The success of the operation relies on the number of pairs (i, j) (1 ≤ i < j ≤ n), such that the distance between watchman i and watchmen j calculated by Doctor Manhattan is equal to the distance between them calculated by Daniel. You were asked to compute the number of such pairs.

Input

The first line of the input contains the single integer n (1 ≤ n ≤ 200 000) — the number of watchmen.

Each of the following n lines contains two integers x_i and y_i (|x_i|, |y_i| ≤ 10⁹).

Some positions may coincide.

Output

Print the number of pairs of watchmen such that the distance between them calculated by Doctor Manhattan is equal to the distance calculated by Daniel.

Examples

Input

3
1 1
7 5
1 5

Output

2

Input

6
0 0
0 1
0 2
-1 1
0 1
1 1

Output

11

Note

In the first sample, the distance between watchman 1 and watchman 2 is equal to |1 - 7| + |1 - 5| = 10 for Doctor Manhattan and 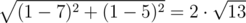 for Daniel. For pairs (1, 1), (1, 5) and (7, 5), (1, 5) Doctor Manhattan and Daniel will calculate the same distances.

题意就是曼哈顿距离和欧几里得距离，自己把公式随便算一算就得出要在同一个横坐标或者是同一个纵坐标的才成立，然后就可以用握手问题的那个公式，再把重复的相同的位置去掉就可以。

然而握手问题的公式我不会写。。。所以想了一个其他的，代码看一下就会懂的。。。

要用long long。。。

然后就是排序的时候要注意！！！别写错了==,wa在排序写错了。。。

代码:

#include<bits/stdc++.h>
using namespace std;
const int N=2*1e7;
typedef long long ll;
struct node{
  int a,b;
}dis[N];
bool cmp1(node x,node y){
    if(x.a==y.a)
        return x.b<y.b;
        return x.a<y.a;
}
bool cmp2(node x,node y){
    if(x.b==y.b)
        return x.a<y.a;
        return x.b<y.b;
}
int main(){
    int n;
    ll cnt,ans;
    while(~scanf("%d",&n)){
        for(int i=0;i<n;i++)
            scanf("%I64d%I64d",&dis[i].a,&dis[i].b);
            sort(dis,dis+n,cmp1);
            cnt=0;ans=0;
            for(int i=1;i<n;i++){
                if(dis[i].a==dis[cnt].a)
                    ans+=abs(i-cnt);
                else
                    cnt=i;
            }
            cnt=0;
            sort(dis,dis+n,cmp2);
            for(int i=1;i<n;i++){
                if(dis[i].b==dis[cnt].b)
                    ans+=abs(i-cnt);
                else
                    cnt=i;
            }
            cnt=0;
            for(int i=1;i<n;i++){
                if(dis[i].a==dis[cnt].a&&dis[i].b==dis[cnt].b)
                    ans-=abs(i-cnt);
                else
                    cnt=i;
            }
            printf("%I64d\n",ans);
    }
    return 0;
}