Yang, McKee - OIT and Indirect Shadows(SIGGRAPH 2010 Advanced RealTime Rendering Course).pptx

最近又发现了好东西

mark

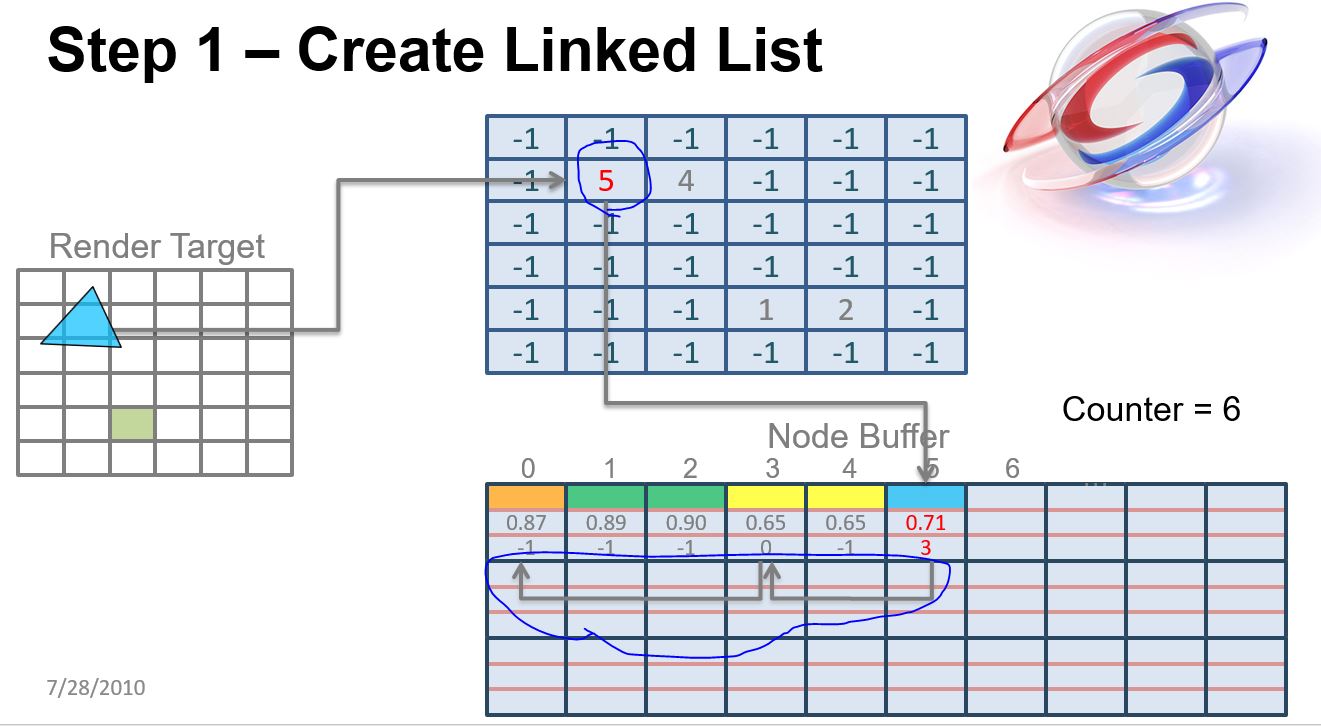
注意画圈的地方 向前的指针 所以只存链表尾部节点到 pixel就可以 比如用5覆盖3 通过node buffer的指针可以找回去

order-independent transparency & programmable blending的更多相关文章

  1. [ZZ] KlayGE 游戏引擎 之 Order Independent Transparency（OIT）

    转载请注明出处为KlayGE游戏引擎,本文的永久链接为http://www.klayge.org/?p=2233 http://dogasshole.iteye.com/blog/1429665 ht ...

  2. Order Independent Transparency

    http://on-demand.gputechconf.com/gtc/2014/presentations/S4385-order-independent-transparency-opengl. ...

  3. metal2 里 programmable blending 和image block的区别 语法以及persistent thread group的语法

    programmable blending 刚接触这个概念的时候 挺激动的 因为能解决很多管线里面的问题 比如 切一次rt再切回来 为了做read write same rt 有了这个 就不用切啦 可 ...

  4. Wikipedia : OIT history

    http://en.wikipedia.org/wiki/Order-independent_transparency Order-independent transparency From Wiki ...

  5. Intel OIT demo

    https://software.intel.com/en-us/blogs/2013/07/18/order-independent-transparency-approximation-with- ...

  6. Single Depth peeling 顺序无关渲染(OIT)

    什么是顺序无关渲染 在3D渲染中,物体的渲染是按一定的顺序渲染的,这也就可能导致半透明的物体先于不透明的物体渲染,结果就是可能出现半透明物体后的物体由于深度遮挡而没有渲染出来.对于这种情况通常会先渲染 ...

  7. CSharpGL(22)实现顺序无关的半透明渲染(Order-Independent-Transparency)

    +BIT祝威+悄悄在此留下版了个权的信息说: CSharpGL(22)实现顺序无关的半透明渲染(Order-Independent-Transparency) 在 GL.Enable(GL_BLEND ...

  8. MSAA

    多重采样抗锯齿(MultiSampling Anti-Aliasing,簡稱MSAA)是一种特殊的超级采样抗锯齿(SSAA).MSAA首先来自于OpenGL.具体是MSAA只对Z缓存(Z-Buffer ...

  9. iOS苹果官方Demo合集

    Mirror of Apple’s iOS samples This repository mirrors Apple’s iOS samples. Name Topic Framework Desc ...

随机推荐

  1. python录音并调用百度语音识别接口

    #!/usr/bin/env python import requests import json import base64 import pyaudio import wave import os ...

  2. C# String与Byte数组的转换

    string转byte[]: byte[] byteArray = System.Text.Encoding.Default.GetBytes(str); byte[] byteArray = Enc ...

  3. jinfo 命令

    NAME jinfo - Generates configuration information. SYNOPSIS jinfo [ option ] pid 示例:jinfo 3245

  4. 【Python】【基础知识】【内置常量】

    Python的内置常量有: False.True.None.NotImplemented.Ellipsis.__debug__ 由 site 模块添加的常量:quit.exit.copyright.c ...

  5. Java判断指定日期是否为工作日

    Java判断指定日期是否为工作日 转自:https://www.jianshu.com/p/966659492f2f 转:https://www.jianshu.com/p/05ccb5783f65转 ...

  6. 小菜鸟之HTML第二课

    JavaScript 运行在浏览器上的一种基于对象和事件的驱动的脚本语言 基于对象(windows – document location histroy 便于调用对象属性和方法 事件驱动 键盘和鼠标 ...

  7. # codeblocks 使用技巧+伪单文件编译

    codeblocks 使用技巧+伪单文件编译 shift+F2打开和隐藏左侧工作空间 F2 打开和隐藏下面控制台 CTRL+Shift+c 注释,CTRL+Shift+x取消注释 view->p ...

  8. Javascript——数据类型 和 注释

    数据类型:JavaScript中包括如下7种数据类型:字符串.数字.布尔.数组.对象.null.undefined 字符串: 注意:字符串类型的数据需要使用单引号或双引号引起来. 数字: 注意:Jav ...

  9. dev GridView 的组计和分组计

    /// <summary> /// //添加组计 /// </summary> private void SetGroupSummary(GridView gv, string ...

  10. CentOS7 yum安装Mariadb

    1.安装Mariadb #yum -y install mariadb mariadb-server 1.1当执行程序末端显示Complete则完成安装 2.安装完成后启动服务 # systemctl ...