采用霍夫曼编码(Huffman)画出字符串各字符编码的过程并求出各字符编码 --多媒体技术与应用

题目：有一个字符串：cabcedeacacdeddaaaba，问题：

（1）采用霍夫曼编码画出编码的过程，并写出各字符的编码

（2）根据求得的编码，求得各编码需要的总位数

（3）求出整个字符串总编码长度，并计算出字符串位数在编码前与编码后的比值

解答：
（1）各字符出现频率统计如下表所示。
|符号 |出现次数 |出现频率|
|--|--|--|
| a |7|0.35|
|b|2|0.1|
|c|4|0.2|
|d|4|0.2|
|e|3|0.15|
编码过程如下图所示：

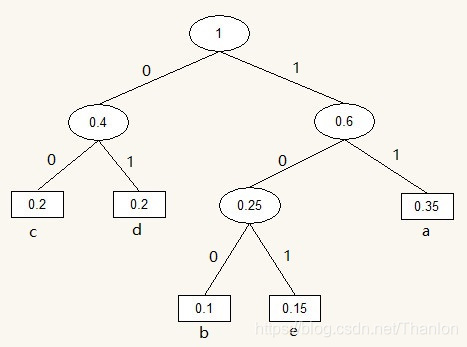
各字符编码如下表所示：
|符号|编码（码字） |
|--|--|
| a | 11 |
| b| 100 |
| c| 00 |
| d| 01|
| e|101 |
（2）由（1）可进一步知道字符编码的码长和需要的位数
|符号|符号出现次数 |概率|编码（码字）|码长|需要的位数
|--|--|--|--|--|--
| a |7|0.35|11|2|14
|b|2|0.1|100|3|6
|c|4|0.2|00|2|8
|d|4|0.2|01|2|8
|e|3|0.15|101|3|9
根据求得的编码，求得各编码需要的总位数是：45位（14+6+8+8+9=45）。
（3）字符串总编码长度：60bit（20 x 3 = 60)。
编码前与编码后的比值：4/3（编码前是60，编码后是45）