机器学习作业（四）神经网络参数的拟合——Python(numpy)实现

题目下载【传送门】

题目简述：识别图片中的数字，训练该模型，求参数θ。

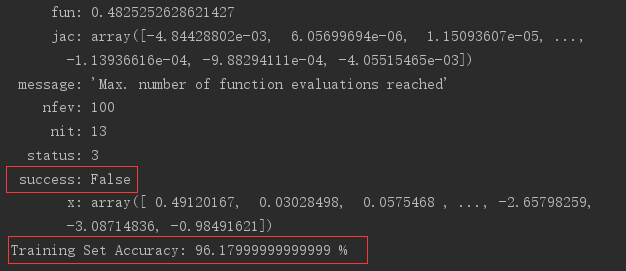
出现了一个问题：虽然训练的模型能够有很好的预测准确率，但是使用minimize函数时候始终无法成功，无论设计的迭代次数有多大，如下图：

 import numpy as np
 import scipy.io as scio
 import matplotlib.pyplot as plt
 import scipy.optimize as op

 # X:5000*400
 # Y:5000*10
 # a1:5000*401（后5000*400）
 # z2:5000*25
 # a2:5000*26（后5000*25）
 # z3:5000*10
 # a3:5000*10
 # Theta1:25*401
 # Theta2:10*26
 # delta3:5000*10
 # delta2:5000*25
 # bigDelta1:25*401
 # bigDelta2:10*26
 # Theta1_grad:25*401
 # Theta2_grad:10*26

 #显示图片数据
 def displayData(X):
     m = np.size(X, 0)  #X的行数，即样本数量
     n = np.size(X, 1)  #X的列数，即单个样本大小
     example_width = int(np.round(np.sqrt(n)))  #单张图片宽度
     example_height = int(np.floor(n / example_width))  #单张图片高度
     display_rows = int(np.floor(np.sqrt(m)))  #显示图中，一行多少张图
     display_cols = int(np.ceil(m / display_rows))  #显示图中，一列多少张图片
     pad = 1  #图片间的间隔
     display_array = - np.ones((pad + display_rows * (example_height + pad),
                             pad + display_cols * (example_width + pad)))  #初始化图片矩阵
     curr_ex = 0  #当前的图片计数
     #将每张小图插入图片数组中
     for j in range(0, display_rows):
         for i in range(0, display_cols):
             if curr_ex >= m:
                 break
             max_val = np.max(abs(X[curr_ex, :]))
             jstart = pad + j * (example_height + pad)
             istart = pad + i * (example_width + pad)
             display_array[jstart: (jstart + example_height), istart: (istart + example_width)] = \
                 np.array(X[curr_ex, :]).reshape(example_height, example_width) / max_val
             curr_ex = curr_ex + 1
         if curr_ex >= m:
             break
     display_array = display_array.T
     plt.imshow(display_array,cmap=plt.cm.gray)
     plt.axis('off')
     plt.show()

 #计算hθ(z)
 def sigmoid(z):
     g = 1.0 / (1.0 + np.exp(-z))
     return g

 #初始化Θ，保持在[-ε，ε]
 def randInitializeWeights(sizeList):
     epsilon_init = 0.12
     theta1_lx = sizeList['theta1_lx']
     theta1_ly = sizeList['theta1_ly']
     theta2_lx = sizeList['theta2_lx']
     theta2_ly = sizeList['theta2_ly']
     theta_size = theta1_lx * theta1_ly + theta2_lx * theta2_ly
     W = np.random.uniform(-epsilon_init, epsilon_init, theta_size)
     return W

 #把一维的矩阵改写为多维
 def changeForm(theta_vector, theta1_lx, theta1_ly, theta2_lx, theta2_ly):
     theta1 = np.array(theta_vector[0: theta1_lx * theta1_ly]).reshape(theta1_lx, theta1_ly)
     theta2 = np.array(theta_vector[theta1_lx * theta1_ly: theta1_lx * theta1_ly + theta2_lx * theta2_ly])\
         .reshape(theta2_lx, theta2_ly)
     theta = {'Theta1': theta1, 'Theta2': theta2}
     return theta

 #计算正向激励的参数a
 def computeA(nn_params, X):
     theta1 = nn_params['Theta1']
     theta2 = nn_params['Theta2']
     m = np.size(X, 0)

     #第二层计算
     one = np.ones(m)
     a1 = np.insert(X, 0, values=one, axis=1)
     a2 = sigmoid(np.dot(a1, theta1.T))
     #第三层计算
     one = np.ones(np.size(a2, 0))
     a2 = np.insert(a2, 0, values=one, axis=1)
     a3 = sigmoid(np.dot(a2, theta2.T))
     a_res = {'a1': a1, 'a2': a2, 'a3': a3}
     return a_res

 #计算g'(z)
 def sigmoidGradient(z):
     g = np.multiply(sigmoid(z), 1 - sigmoid(z))
     return g

 #计算 J
 def nnCostFunction(nn_params, X, Y, lamb, sizeList):
     theta = changeForm(nn_params,
                        sizeList['theta1_lx'], sizeList['theta1_ly'],
                        sizeList['theta2_lx'], sizeList['theta2_ly'])
     theta1 = theta['Theta1']
     theta2 = theta['Theta2']
     m = np.size(X, 0)
     a_res = computeA(theta, X)
     a3 = a_res['a3']
     #计算J
     J = 1 / m * np.sum(-np.multiply(Y, np.log(a3)) - np.multiply((1 - Y), np.log(1 - a3)))
     #规格化
     theta1_copy = theta1[:, 1:]
     theta2_copy = theta2[:, 1:]
     J = J + lamb / (2 * m) * (np.sum(theta1_copy ** 2) + np.sum(theta2_copy ** 2))
     print(J)
     return J

 #计算 D
 def nnGradient(nn_params, X, Y, lamb, sizeList):
     theta = changeForm(nn_params,
                        sizeList['theta1_lx'], sizeList['theta1_ly'],
                        sizeList['theta2_lx'], sizeList['theta2_ly'])
     theta1 = theta['Theta1']
     theta2 = theta['Theta2']
     m = np.size(X, 0)
     a_res = computeA(theta, X)
     a1 = a_res['a1']
     a2 = a_res['a2']
     a3 = a_res['a3']
     theta1_copy = theta1[:, 1:]
     theta2_copy = theta2[:, 1:]
     #计算δ
     delta3 = a3 - Y
     delta2 = np.multiply(np.dot(delta3, theta2_copy), sigmoidGradient(np.dot(a1, theta1.T)))
     #计算Δ
     bigDeilta1 = np.dot(delta2.T, a1)
     bigDeilta2 = np.dot(delta3.T, a2)
     #计算D
     theta1_grad = bigDeilta1 / m + lamb / m * theta1
     theta2_grad = bigDeilta2 / m + lamb / m * theta2
     theta1_grad[:, 0] = bigDeilta1[:, 0] / m
     theta2_grad[:, 0] = bigDeilta2[:, 0] / m
     #当使用高级优化方法来优化神经网络时，需要将多个参数矩阵展开，才能传入优化函数
     grad = np.r_[theta1_grad.flatten(), theta2_grad.flatten()]
     # print(np.size(grad))
     return grad

 #测试参数的初始化
 def debugInitializeWeights(L_out, L_in):
     W = np.arange(1, L_out * (L_in + 1)+1)
     W = np.sin(W)
     W = np.array(W).reshape(L_out, (L_in + 1)) / 10;
     return W

 #数值方法计算梯度
 def computeNumericalGradient(theta, X, Y ,lamb, sizeList):
     numgrad = np.zeros(np.size(theta))
     perturb = np.zeros(np.size(theta))
     e = 1e-4
     for p in range(0, np.size(theta)):
         perturb[p] = e
         theta_minus = theta - perturb
         theta_plus = theta + perturb
         loss1 = nnCostFunction(theta_minus, X, Y, lamb, sizeList)
         loss2 = nnCostFunction(theta_plus, X, Y, lamb, sizeList)
         numgrad[p] = (loss2 - loss1) / (2 * e)
         perturb[p] = 0
     return numgrad

 #梯度检测函数
 def checkNNGradients(lamb):
     #设置测试参数
     input_layer_size = 3;
     hidden_layer_size = 5;
     num_labels = 3;
     lamb = 1
     m = 5;
     sizeList = {'theta1_lx': hidden_layer_size,
                 'theta1_ly': input_layer_size + 1,
                 'theta2_lx': num_labels,
                 'theta2_ly': hidden_layer_size + 1}  # 保存θ大小的参数
     theta1 = debugInitializeWeights(hidden_layer_size, input_layer_size)
     theta2 = debugInitializeWeights(num_labels, hidden_layer_size)
     theta = np.r_[theta1.flatten(), theta2.flatten()]
     X = debugInitializeWeights(m, input_layer_size - 1)
     y = np.random.randint(0, num_labels, (m, 1))
     # 对y进行改写，改为 m*num_labels 规格的矩阵
     Y = np.zeros((m, num_labels))
     for i in range(0, m):
         Y[i, y[i, 0]] = 1
     grad = nnGradient(theta, X, Y, lamb, sizeList)
     numGrad = computeNumericalGradient(theta, X, Y, lamb, sizeList)
     diff = np.linalg.norm(numGrad - grad) / np.linalg.norm(numGrad + grad)
     print('check NN Gradient: diff = ', diff)

 #使用模型进行预测
 def predict(theta1, theta2, X):
     m = np.size(X,0)
     p = np.zeros((np.size(X, 0), 1))
     #第二层计算
     one = np.ones(m)
     X = np.insert(X, 0, values=one, axis=1)
     a2 = sigmoid(np.dot(X, theta1.T))
     #第三层计算
     one = np.ones(np.size(a2,0))
     a2 = np.insert(a2, 0, values=one, axis=1)
     a3 = sigmoid(np.dot(a2, theta2.T))
     p = a3.argmax(axis=1) + 1  #y的值为1-10，所以此处0-9要加1
     return p.flatten()

 # ——————————————主函数————————————————————
 #初始化数据
 input_layer_size = 400
 hidden_layer_size = 25
 num_labels = 10
 sizeList = {'theta1_lx': hidden_layer_size,
             'theta1_ly': input_layer_size + 1,
             'theta2_lx': num_labels,
             'theta2_ly': hidden_layer_size + 1}  #保存θ大小的参数
 lamb = 1

 #加载数据文件
 data = scio.loadmat('ex4data1.mat')
 X = data['X']
 m = np.size(X, 0)
 y = data['y']
 # 对y进行改写，改为5000*10规格的矩阵，第0-9个位置分别表示1，2，...，9，0
 Y = np.zeros((m, num_labels))
 for i in range(0, m):
     Y[i, y[i, 0] - 1] = 1
 rand_indices = np.random.randint(0, m, 100)
 sel = X[rand_indices, :]
 displayData(sel)

 #测试数据θ
 theta = scio.loadmat('ex4weights.mat')
 theta1 = theta['Theta1']
 theta2 = theta['Theta2']
 nn_theta = np.r_[theta1.flatten(), theta2.flatten()]

 #测试nnCostFunction
 # J = nnCostFunction(nn_theta, X, Y, 3, sizeList)
 # print(J)

 #测试nnGradient
 print(nnGradient(nn_theta, X, Y, lamb, sizeList))

 #初始化参数
 nn_params = randInitializeWeights(sizeList)

 # 梯度检测
 # checkNNGradients(lamb)

 # 训练模型
 res = op.minimize(fun=nnCostFunction,
                   x0=nn_params,
                   args=(X, Y, lamb, sizeList),
                   method='TNC',
                   jac=nnGradient,
                   options={'maxiter': 100})
 print(res)

 #计算准确率
 all_theta = changeForm(res.x, sizeList['theta1_lx'], sizeList['theta1_ly'],
                        sizeList['theta2_lx'], sizeList['theta2_ly'])
 res_theta1 = all_theta['Theta1']
 res_theta2 = all_theta['Theta2']
 pred = predict(res_theta1, res_theta2, X)
 acc = np.mean(pred == y.flatten())*100
 print('Training Set Accuracy:',acc,'%')

 #显示中间隐藏层
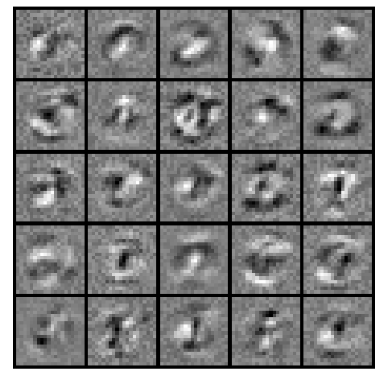
 displayData(res_theta1[:, 1:])

隐藏层显示：