opencv —— Laplacian 拉普拉斯算子、二阶导数用于边缘检测

Laplacian 算子简介

求多元函数的二阶导数的映射又称为 Laplacian 算子:

 

计算拉普拉斯变换：Laplacian 函数

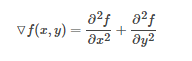
void Laplacian(InputArray src, OutputArray dst, int ddepth, int ksize = 1, double scale = 1, double delta = 0, int borderType = BORDER_DEFAULT);

• src，输入图像，填 Mat 类型即可,但需为单通道 8 位图像。
• dst，输出图像，需要和源图像有一样的尺寸和类型。
• ddepth，输出图像的深度，满足下列要求：

src.depth() = CV_8U, ddepth = -1 / CV_16S / CV_32F / CV_64F

src.depth() = CV_16U / CV_16S, ddepth = -1 / CV_32F / CV_64F

src.depth() = CV_32F, ddepth = -1 / CV_32F / CV_64F

src.depth() = CV_64F, ddepth = -1 / CV_64F

• ksize，表示用于计算二阶导数的滤波器的孔径大小，必须取正奇数。默认值为 1，其实和 3 的效果一样，都采用 3×3 的孔径的滤波器，如下图。

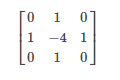
若考虑两个对角线方向的偏导数, 则为:

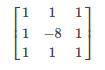
好像只能取 1 和 3，不然算出来的不是近似二阶导数。

• scale，计算拉普拉斯值的时候可选的比例因子，默认值为 1，表示默认情况下不进行缩放。
• delta，输出的拉普拉斯值 = scale * ðf(x,y) + delta。
• borderType，x，y 方向上的滤波器都有一定大小，边缘会处理不到，需要进行边缘扩展。这个参数指定边缘扩充类型。

代码示例：

#include<opencv.hpp>
#include<iostream>
using namespace std;
using namespace cv;
int main() {
    Mat src = imread("C:/Users/齐明洋/Desktop/证件照/6.jpg");
    GaussianBlur(src, src, Size(, ), , );
    imshow("src", src);

    Mat gray, lap_img;
    cvtColor(src, gray, COLOR_BGR2GRAY);
    Laplacian(gray, lap_img, CV_16SC1, );
    convertScaleAbs(lap_img, lap_img);
    imshow("lap_img", lap_img);
    waitKey();
}

效果演示：

借鉴博客：https://www.cnblogs.com/german-iris/p/4840647.html