AcWing 282. 石子合并
#include <iostream>
#include <algorithm>
using namespace std;
const int N = ;
int n;
int s[N];//前缀和
int f[N][N];//状态
int main() {
scanf("%d", &n);
for (int i = ; i <= n; i ++ ) scanf("%d", &s[i]);
for (int i = ; i <= n; i ++ ) s[i] += s[i - ];
//如果区间长度为1,那么合并的代价就为0,所以不用考虑,直接从2开始
for (int len = ; len <= n; len ++ )//枚举区间长度
for (int i = ; i + len - <= n; i ++ ) { //枚举区间起点
int l = i, r = i + len - ;//左右端点
f[l][r] = 1e8;//初始化
for (int k = l; k < r; k ++ )//枚举分界点
f[l][r] = min(f[l][r], f[l][k] + f[k + ][r] + s[r] - s[l - ]);
}
printf("%d\n", f[][n]);
return ;
}
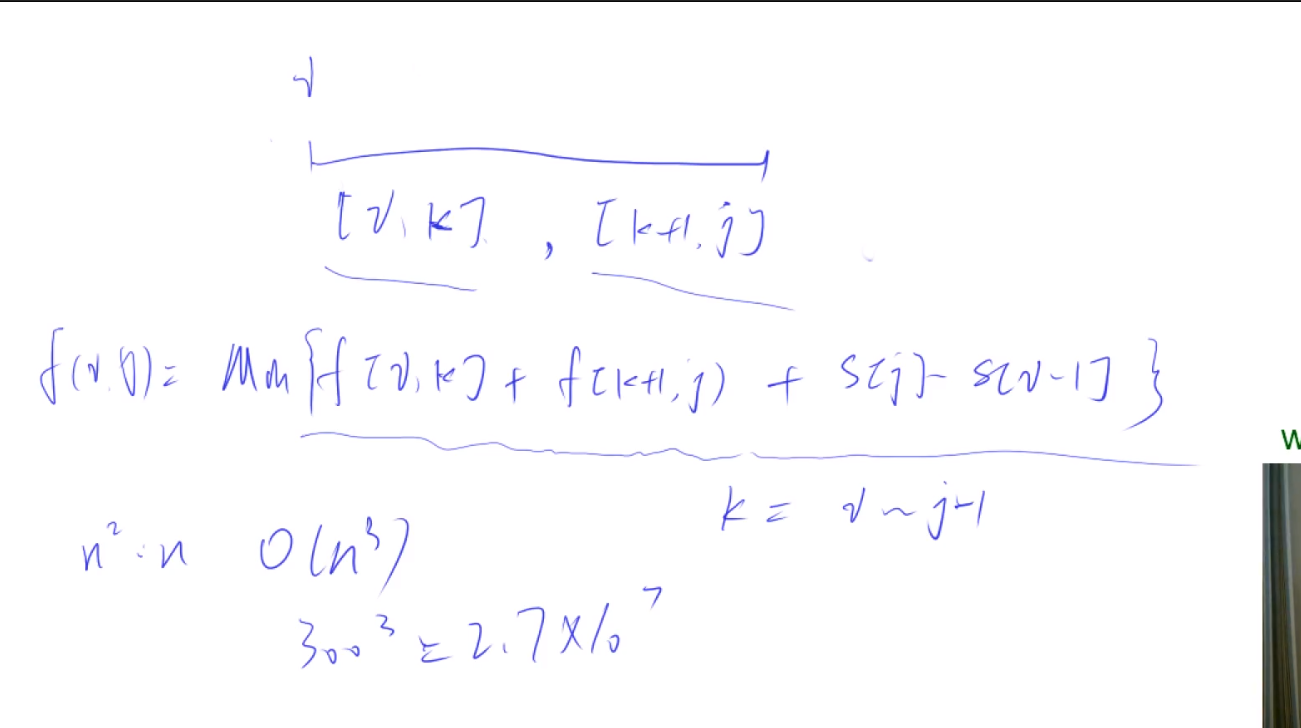

AcWing 282. 石子合并的更多相关文章
- NK 1137: 石子合并问题
1137: 石子合并问题 Time Limit: 1500 ms Memory Limit: 10000 kB Judge type: Multi-cases Total Submit ...
- RQNOJ 490 环形石子合并
题目链接:https://www.rqnoj.cn/problem/490 题目描述 在一个园形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆,并将新的一 ...
- codevs1048 石子合并
题目链接:http://codevs.cn/problem/1048/ 题目描述 Description 有n堆石子排成一列,每堆石子有一个重量w[i], 每次合并可以合并相邻的两堆石子,一次合并的代 ...
- 石子合并[DP-N3]
题目描述 在一个园形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分. 试设计出1个算法,计算出将N堆石子合并成1 ...
- 51Nod 1021 石子合并 Label:Water DP
N堆石子摆成一条线.现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的代价.计算将N堆石子合并成一堆的最小代价. 例如: 1 2 3 4,有 ...
- BZOJ 3229: [Sdoi2008]石子合并
3229: [Sdoi2008]石子合并 时间限制: 3 Sec 内存限制: 128 MB提交: 497 解决: 240[提交][][] 题目描述 在一个操场上摆放着一排N堆石子.现要将石子有次序 ...
- nyoj 737 石子合并(一)。区间dp
http://acm.nyist.net/JudgeOnline/problem.php?pid=737 数据很小,适合区间dp的入门 对于第[i, j]堆,无论你怎么合并,无论你先选哪两堆结合,当你 ...
- BZOJ-3229 石子合并 GarsiaWachs算法
经典DP?稳T 3229: [Sdoi2008]石子合并 Time Limit: 3 Sec Memory Limit: 128 MB Submit: 426 Solved: 202 [Submit] ...
- BZOJ3229 石子合并
Description 在一个操场上摆放着一排N堆石子.现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的得分. 试设计一个算法,计算出将N堆石 ...
随机推荐
- TCP与UDP的一些心得
1:CC攻击是正常的业务逻辑,大并发让你处理不过来,处理XP SP2,以上的系统都封了RAW格式协议封包自定义,除了基于应用层改协议,之外都是模拟或请求来测试传输层2:UDP不会粘包,不会少包,除非缓 ...
- VMware桥接模式下虚拟机ping主机不通
现象: VMware设置为桥接模式,虚拟机ping主机不通,主机ping虚拟机通. 解决: 尝试以下几种方法 关闭主机(专用网络.来宾或公用网络)和虚拟机的防火墙. 更改桥接的物理网卡,确保是主机正在 ...
- 金蝶云星空Python案例地址
https://club.kingdee.com/forum.php?mod=viewthread&tid=1235461
- MyEclipse CI 2019.4 完美激活版(含离线包+激活工具+安装教程)
ps:MyEclipse目前已更新至2019.12.5,但是目前还没有有效的激活方式,本次文章以2019.4为例; 该文章使用离线安装的方式进行安装,在线安装不保证不会出现各类小问题,离线安装包及激活 ...
- react-native简单使用
基本组件的使用介绍 View: Text: TextInput: Image: Button: ActivityIndicator: ScrollView:这是一个列表滚动的组件 ListView:也 ...
- json 的key值不能是变量
var _key = name; var _value = 2; var params = { _key :_ value } _key 为变量 console.log(params); { _key ...
- POJ3723(最小生成树,负权)
题目描述 温迪有一个国家,他想建立一支军队来保护他的国家.他收留了N个女孩和M个男孩,想把她们收留成他的士兵.征兵无特权,必须交纳一万元.女孩和男孩之间有一些关系,温迪可以利用这些关系来降低他的成本. ...
- 题解【AcWing487】金明的预算方案
题面 有依赖的背包问题模板题. 我们观察到 每个主件可以有 0 个.1 个或 2 个附件 , 于是考虑对于每一个主件,我们用枚举子集的方式枚举使用哪一些附件, 然后就是一个经典的分组背包问题了. 注意 ...
- Wannafly Camp 2020 Day 1E 树与路径 - 树上差分,LCA
#include <bits/stdc++.h> using namespace std; #define int long long const int N = 1000005; vec ...
- Failed to set locale, defaulting to C
echo "export LC_ALL=en_US.UTF-8" >> /etc/profile source /etc/profile 没有设置local环境
