[洛谷P3621] [APIO2007] 风铃

Description

你准备给弟弟 Ike 买一件礼物，但是，Ike 挑选礼物的方式很特别：他只喜欢那些能被他排成有序形状的东西。

你准备给 Ike 买一个风铃。风铃是一种多层的装饰品，一般挂在天花板上。

每个风铃都包含一些由竖直线连起来的水平杆。每根杆的两头都有线连接，下面或者挂着另一根水平杆，或者挂着一个玩具。下面是一个风铃的例子：

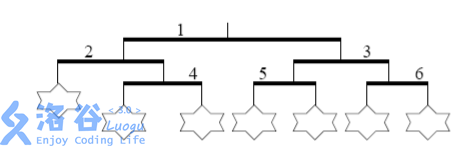
为了满足弟弟，你需要选一个满足下面两个条件的风铃：

(1) 所有的玩具都在同一层(也就是说，每个玩具到天花板之间的杆的个数是一样的)或至多相差一层。

(2) 对于两个相差一层的玩具，左边的玩具比右边的玩具要更靠下一点。

风铃可以按照下面的规则重新排列：任选一根杆，将杆两头的线“交换”。也就是解开一根杆左右两头的线，然后将它们绑到杆的另一头。这个操作不会改变更下面的杆上线的排列顺序。正在训练信息学奥林匹克的你，决定设计一个算法，判断能否通过重新排列，将一个给定的风铃变为 Ike 喜欢的样子。

考虑上面的例子，上图中的风铃满足条件(1)，却不满足条件(2)——最左边的那个玩具比它右边的要高。

但是，我们可以通过下面的步骤把这个风铃变成一个 Ike 喜欢的：

第一步，将杆 1 的左右两边交换，这使得杆 2 和杆 3 的位置互换，交换的结果如下图所示：

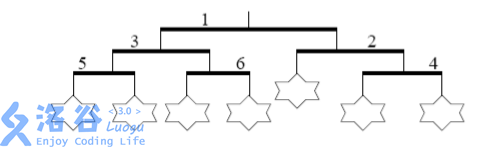
第二步，也是最后一步，将杆 2 的左右两边交换，这使得杆 4 到了左边，原来在左边的玩具到了右边，交换的结果发下图所示：

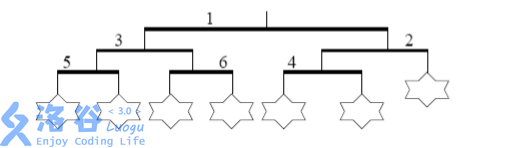
现在的这个风铃就满足 Ike 的条件了。

你的任务是：给定一个风铃的描述，求出最少需要多少次交换才能使这风铃满足 Ike 的条件(如果可能)

Input

输入的第一行包含一个整数 n(1≤n≤100 000)，表示风铃中有多少根杆。

接下来的 n 行描述杆的连接信息。这部分的第 i 行包含两个由空格分隔的整数 li和 ri，描述杆 i 的左右两边悬挂的东西。如果挂的是一个玩具，则对应的值为-1，否则为挂在下面的杆的编号

Output

输出仅包含一个整数。表示最少需要多少次交换能使风铃满足 Ike 的条件。如果不可能满足，输出-1。

Sample Input

6

2 3

-1 4

5 6

-1 -1

-1 -1

-1 -1

Sample Output

2

---

想法

才不会说我是看这个题目好玩才去做的呢

这个题目让我想起了林清玄的散文《风铃》：

有了风铃，风虽然吹过了，还留下美妙的声音

有了心的风铃，生命即使走过了，也会留下动人的痕迹

每一次起风的时候，每一步岁月的脚步，都会那样真实地存在。

等等，跑题了！

这个题就是树形dp嘛，注意判断几种不行的情况：

1.风铃相差层数>1

2.在满足风铃相差层数为1的情况下，把在上面一层的风铃统称为F，把下面一层的风铃统称为G

在某一节点，其两个子节点中都既有F又有G

然后注意各种细节就好了（自古树形dp细节多qwq）

---

代码

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

const int N = 100005;

int ch[N][2],pa[N],dep[N];
int n,rt;

int m,d[N],t;
void get_dep(int u){
    for(int i=0;i<2;i++){
        if(ch[u][i]!=-1){
            dep[ch[u][i]]=dep[u]+1;
            get_dep(ch[u][i]);
        }
        else d[m++]=dep[u]+1,t=max(t,d[m-1]);
    }
}
int sz[N],num[N]; //num表示该节点子树中F与G的总和，sz表示该节点子树中F个数
void dfs0(int u){
    for(int i=0;i<2;i++){
        if(ch[u][i]!=-1){
            dfs0(ch[u][i]);
            num[u]+=num[ch[u][i]]; sz[u]+=sz[ch[u][i]];
        }
        else {
            num[u]++;
            if(dep[u]+1==t-1) sz[u]++;
        }
    }
}

int flag;
int dfs(int u){
    if(sz[u]==0 || sz[u]==num[u]) return 0;
    if(ch[u][0]!=-1 && ch[u][1]!=-1){
        if(sz[ch[u][0]]==0) return dfs(ch[u][1]);
        if(sz[ch[u][1]]==0) return dfs(ch[u][0])+1;
        if(sz[ch[u][0]]==num[ch[u][0]]) return dfs(ch[u][1])+1;
        if(sz[ch[u][1]]==num[ch[u][1]]) return dfs(ch[u][0]);
        flag=0; return 0;
    }
    if(ch[u][0]==-1 && ch[u][1]!=-1){
        if(sz[ch[u][1]]==0) return 1;
        return dfs(ch[u][1])+1;
    }
    if(ch[u][0]!=-1 && ch[u][1]==-1){
        if(sz[ch[u][0]]==0) return 0;
        return dfs(ch[u][0]);
    }
    return 0;
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d",&ch[i][0],&ch[i][1]);
        if(ch[i][0]!=-1) pa[ch[i][0]]=i;
        if(ch[i][1]!=-1) pa[ch[i][1]]=i;
    }

    for(int i=1;i<=n;i++) if(!pa[i]) { rt=i; break; }
    dep[rt]=1; get_dep(rt);

    flag=1;
    for(int i=0;i<m;i++) if(d[i]<t-1) flag=0;
    if(flag==0) { printf("-1"); return 0; }

    dfs0(rt);
    if(sz[rt]==0) { printf("0"); return 0; }

    int ans=dfs(rt);
    if(flag==0) printf("-1");
    else printf("%d",ans);

    return 0;
}