【NOI2010】能量采集

题面

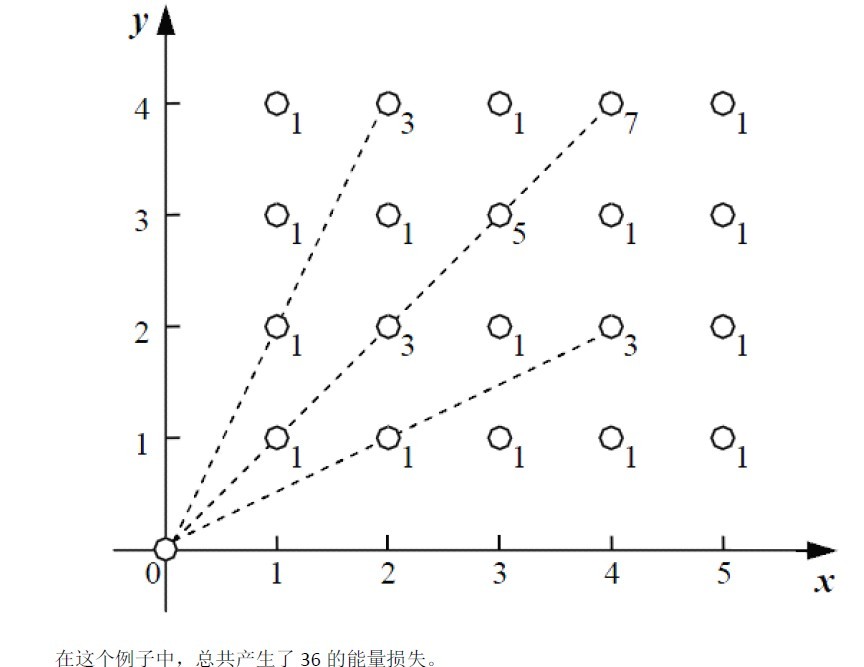
题目分析

对于第\((i,j)\)个位置，对答案的贡献为\(2*gcd(i,j)-1\)。

所以有\(ans=2*\sum\limits_{i=1}^n\sum\limits_{j=1}^mgcd(i,j)-n*m\)。

其中\(\sum\limits_{i=1}^n\sum\limits_{j=1}^mgcd(i,j)=\sum\limits_{d=1}^nd\sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)==d]\)

转化为求\(gcd(i,j)==d\)的对数，方法与【BZOJ2818】Gcd相同。

代码实现

#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdio>
#include<iomanip>
#include<cstdlib>
#define MAXN 0x7fffffff
typedef long long LL;
const int N=100005;
using namespace std;
inline int Getint(){register int x=0,f=1;register char ch=getchar();while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}return x*f;}
int mu[N],prime[N];
bool vis[N];
int main(){
	int n=Getint(),m=Getint();if(n>m)swap(n,m);
	mu[1]=1;
	for(int i=2;i<=n;i++){
		if(!vis[i])prime[++prime[0]]=i,mu[i]=-1;
		for(int j=1;j<=prime[0]&&1ll*i*prime[j]<=n;j++){
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)break;
			mu[i*prime[j]]=-mu[i];
		}
	}
	LL ans=0;
	for(int d=1;d<=n;d++){
		LL ret=0;
		for(int x=1;x*d<=n;x++)
			ret+=1ll*mu[x]*(n/x/d)*(m/x/d);
		ans+=ret*d;
	}
	cout<<2*ans-1ll*n*m;
	return 0;
}