Fisher精确检验【转载】

转自：https://en.wikipedia.org/wiki/Fisher%27s_exact_test

https://www.cnblogs.com/Dzhouqi/p/3440575.html

1.定义

Fisher's exact test( 费希尔精确检验)

是用于分析列联表（contingency tables）统计显著性检验方法，它用于检验两个分类的关联（association)。虽然实际中常常使用于小数据情况，但同样适用于大样本的情况。

//显著性检验都和P值挂钩。

2.例子

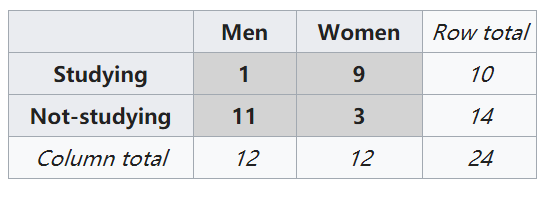
想探求女人和男人之间学习与不学习是否有差异，原假设是不存在差异。

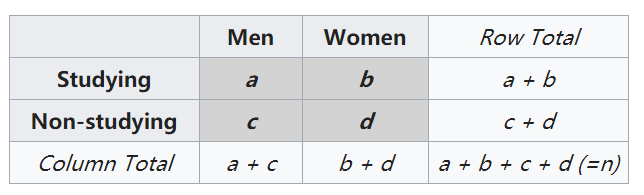
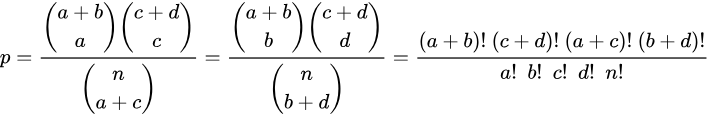
那么给定的这个例子使用上述计算P值得：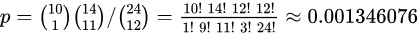

那么计算得到的p值是小的，越小越能拒绝原假设。

即在原假设为真的情况下，当前使用的数据得到的结果却P值是小的，（样本代表总体吧），说明是样本（总体）是出现了小概率事件，那么原来的假设很有可能是存在问题的。小概率时间都出现了。

3.R中实现

> fisher.test(rbind(c(,),c(,)), alternative="less")$p.value
[] 0.001379728

为什么只计算其中一类就可以了？

因为这个列联表得自由度是1，比如第一行中如果有一个是确定的，那么因为和是定值，所以另一个数也就确定了。

//但是这个P值真的是越小越能表示那个啥吗？他有单调性？

//不过从分子来看，b和d和是一定的，那么，如果两者差值越大，对应的二项式系数都会越小。那么分子就会越小。但是分母并不是这个规律。a和b在变小变大的过程中会有一个趋势。

4.为什么P值越小显著性越高？

维基百科上给出了一个例子来说明：

这个例子中明显是有分布差异的。

由上述计算得到的结果：

> fisher.test(rbind(c(,),c(,)), alternative="less")$p.value
[] 3.36519e-05

所以就说明了，P值越小，显著性越高。