机器学习理论基础学习10--- 高斯混合模型GMM

一、什么是高斯混合模型？

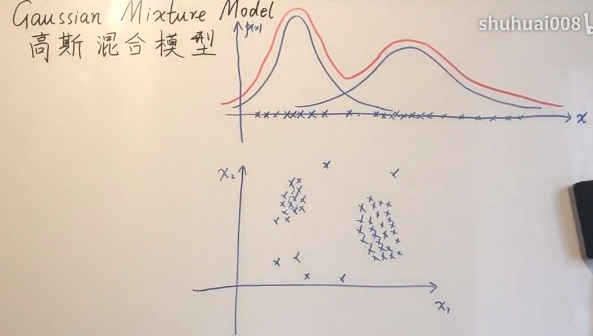
　　高斯混合模型(Gaussian Mixed Model)指的是多个高斯分布函数的线性组合，理论上GMM可以拟合出任意类型的分布，通常用于解决同一集合下的数据包含多个不同的分布的情况（或者是同一类分布，但参数不同，或者是不同类型的分布，比如正态分布和伯努利分布）。

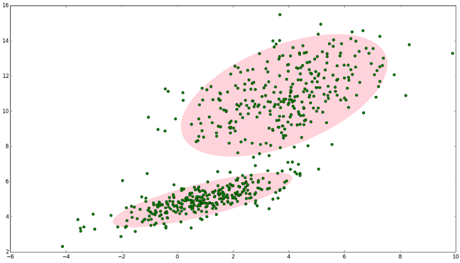上图中的点在我们看来明显分成两个聚类。这两个聚类的点分别通过两个不同的正态分布随机生成而来。但是如果没有GMM,那么只能用一个二维正态分布来描述图1中的数据。图1中的椭圆即为二倍标准差的正态分布椭圆。这显然不太合理，毕竟肉眼一看就觉得应该把它们分成两类。	上图，数据在平面上的空间分布和左图一样，这时使用两个二维高斯分布来描述图中的数据，分别记作 　　　　　　 　　图中的两个椭圆分别是这两个高斯分布的二倍标准差椭圆。可以看到使用两个二维高斯分布来描述图中的数据显然更合理。实际上图中的两个聚类的中的点是通过两个不同的正态分布随机生成而来。 　　如果将两个二维高斯分布合成一个二维的分布，那么就可以用合成后的分布来描述图2中的所有点。最直观的方法就是对这两个二维高斯分布做线性组合，用线性组合后的分布来描述整个集合中的数据。这就是高斯混合模型（GMM）。

1、从几何角度来看：加权平均 ---> 多个高斯分布叠加而成

2、从混合模型角度来看：生成模型

N个样本  x1,x2,...,xN

x是observed variable

z是latent variable，对应着样本x是属于哪一个高斯分布，（离散随机变量）

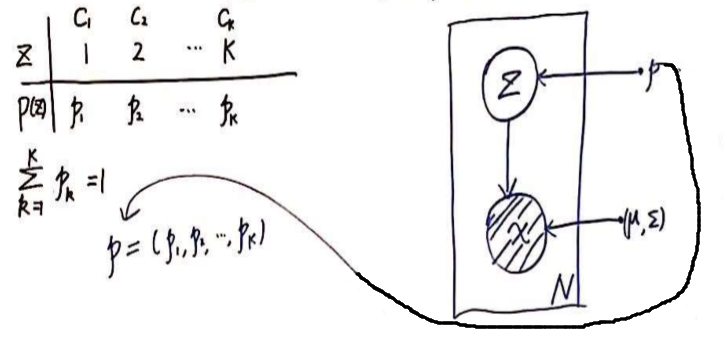
从图上可以看出，任意一个样本，都可能来自任意一个分布，只是来自任意一个分布的权重是有大有小的。

二、怎么求解高斯混合模型？

1、直接使用MLE，无法得出解析解

2、改用EM求解

 最后结果如下：

三、GMM总结

优点：

(1)可以给出一个样本属于某类的概率；
(2)不仅可以用于聚类，还可以用于概率密度的估计；
(3)可以用于生产新的样本点

缺点：
(1)需要确定K值
(2)使用EM算法来求解，往往只能收敛于局部最优；