Opencv Convex Hull (凸包)
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
Mat img1, img2, img3, img4, img_result, img_gray1, img_gray2, img_gray3, img_canny1;
char win1[] = "window1";
char win2[] = "window2";
char win3[] = "window3";
char win4[] = "window4";
char win5[] = "window5";
int thread_value = 100;
int max_value = 255;
RNG rng1(12345);
int Demo_Convex_Hull();
void Demo_1(int, void*);
//发现凸包
int Demo_Convex_Hull()
{
namedWindow(win1, CV_WINDOW_AUTOSIZE);
namedWindow(win2, CV_WINDOW_AUTOSIZE);
//namedWindow(win3, CV_WINDOW_AUTOSIZE);
img1 = imread("D://images//1//temp2.jpg");
//img2 = imread("D://images//1//p5_1.jpg");
if (img1.empty())
{
cout << "could not load image..." << endl;
return 0;
}
imshow(win1, img1);
img4 = Mat::zeros(img1.size(),CV_8UC3);
//转灰度图
cvtColor(img1, img_gray1, CV_BGR2GRAY);
//模糊处理
blur(img_gray1, img2, Size(3, 3), Point(-1, -1),BORDER_DEFAULT);
createTrackbar("track", win1, &thread_value, max_value, Demo_1);
Demo_1(0,0);
return 0;
}
void Demo_1(int,void*)
{
vector<vector<Point>> vec_p;
vector<Vec4i> vec_4i;
threshold(img2, img3, thread_value, max_value, THRESH_BINARY);
findContours(img3, vec_p, vec_4i, RETR_TREE, CHAIN_APPROX_SIMPLE, Point(0, 0));
vector<vector<Point>> convexs(vec_p.size());
for (size_t i=0;i<vec_p.size();i++)
{
convexHull(vec_p[i], convexs[i], false, true);
}
for (size_t j=0;j<vec_p.size();j++)
{
Scalar color_1 = Scalar(rng1.uniform(0,255), rng1.uniform(0, 255), rng1.uniform(0, 255));
drawContours(img4, vec_p, j, color_1, 2, LINE_8, vec_4i, 0, Point(0, 0));
drawContours(img4, convexs, j, color_1, 2, LINE_8, vec_4i, 0, Point(0, 0));
}
imshow(win2,img4);
}
int main()
{
Demo_Convex_Hull();
waitKey(0);
return 0;
}
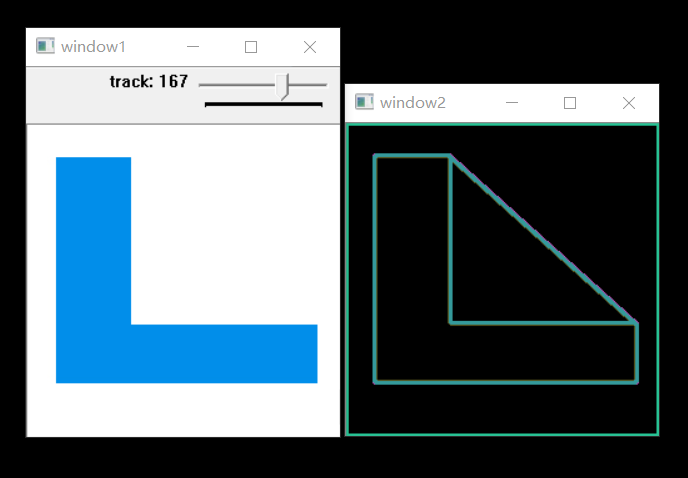
Opencv Convex Hull (凸包)的更多相关文章
- [GYM 100492A] Average Convex Hull 凸包好题
大致题意: 给出一个点集,其中有一个点有相同的几率会被删除,求删除之后的点集够成的凸包上的点的平均数. 首先看到题目,可以考虑枚举删除的点,将其凸包上前后两点以及两点间凸包内所有点构建凸包,因为凸包内 ...
- 2.2 convex hull凸包
1.定义:一组平面上的点,求一个包含所有点的最小的凸多边形,就是凸包问题. 利用编程解决凸包问题,应该得到一组逆时针的顶点的顺序集合,在边上但不是顶点,则不包含在集合里. 2.机械的方法:将点所在的位 ...
- P6810 「MCOI-02」Convex Hull 凸包
Link 一句话题意: 求出 \(\displaystyle\sum_{i=1}^{n}\sum_{j=1}^{m}\tau(i)\tau(j)\tau(gcd(i,j))\) 前置知识 \(diri ...
- 【题解】「MCOI-02」Convex Hull 凸包
题目戳我 \(\text{Solution:}\) \[\sum_{i=1}^n \sum_{j=1}^n \rho(i)\rho(j)\rho(\gcd(i,j)) \] \[=\sum_{d=1} ...
- OpenCV入门之寻找图像的凸包(convex hull)
介绍 凸包(Convex Hull)是一个计算几何(图形学)中的概念,它的严格的数学定义为:在一个向量空间V中,对于给定集合X,所有包含X的凸集的交集S被称为X的凸包. 在图像处理过程中,我们 ...
- opencv::凸包-Convex Hull
概念介绍 什么是凸包(Convex Hull),在一个多变形边缘或者内部任意两个点的连线都包含在多边形边界或者内部. 正式定义:包含点集合S中所有点的最小凸多边形称为凸包 Graham扫描算法 首先选 ...
- 凸包(Convex Hull)构造算法——Graham扫描法
凸包(Convex Hull) 在图形学中,凸包是一个非常重要的概念.简明的说,在平面中给出N个点,找出一个由其中某些点作为顶点组成的凸多边形,恰好能围住所有的N个点. 这十分像是在一块木板上钉了N个 ...
- Monotone Chain Convex Hull(单调链凸包)
Monotone Chain Convex Hull(单调链凸包)算法伪代码: //输入:一个在平面上的点集P //点集 P 按 先x后y 的递增排序 //m 表示共a[i=0...m]个点,ans为 ...
- OpenCV学习(29) 凸包(convexhull)
在opencv中,通过函数convexHulll能很容易的得到一系列点的凸包,比如由点组成的轮廓,通过convexHull函数,我们就能得到轮廓的凸包.下面的图就是一些点集的凸包. 求凸包的代码如下: ...
随机推荐
- linux下如何添加一个用户并且让用户获得root权限【转载】
原文:http://www.cnblogs.com/johnw/p/5499442.html 1.添加用户,首先用adduser命令添加一个普通用户,命令如下: #adduser tommy //添加 ...
- 【转】Linux动态链接(4)ldd与ldconfig
原文网址:http://tsecer.blog.163.com/blog/static/15018172012414105551345/ 一.动态链接工具ldd和ldconfig是动态链接的两个重要辅 ...
- 使用RawComparator加速Hadoop程序
使用RawComparator加速Hadoop程序 在前面两篇文章[1][2]中我们介绍了Hadoop序列化的相关知识,包括Writable接口与Writable对象以及如何编写定制的Writable ...
- printf()_scanf()_取余运算符与取模运算符
基本的输入和输出函数的用法 printf();四种用法 1.printf("字符串\n"); 2.printf("输出控制符",输出参数); 3.printf( ...
- Springboot监控之一:SpringBoot四大神器之Actuator之2--springboot健康检查
Health 信息是从 ApplicationContext 中所有的 HealthIndicator 的 Bean 中收集的, Spring Boot 内置了一些 HealthIndicator. ...
- Vue踩坑记录册
1.vue-cli+webpack项目 修改项目名称 解决办法: 1 删除 node_modules 文件夹(如果修改项目名称,需要在在package.json中修改对应的name) 2 重新安装依赖 ...
- Nmon、nmon analyse安装及使用
性能监控算是性能测试中的一部分,测试人员需要去分析各类系统指标,CPU.网络.内存.磁盘I/O等等.嗯.通常linux系统下有诸如top.netstat.iostat等命令进行查看:而有时需要看某数据 ...
- orzdba_monitor.sh脚本使用
1.orzdba_monitor.sh脚本使用 ./orzdba_monitor.sh 主要是用nohup同时在后台调用orzdba,启动下面三个命令 [root@node02 scripts]# p ...
- XML的学习
XML是可扩展标记语言德意思,它和HTML一样都是标记语言(标签语言),不同之处在于XML可拓展,何为可拓展?在HTML中每个标签都有其特定的含义,我们不可以随便写一个标签并赋予其意义,而XML中就可 ...
- C 语言 - 逻辑运算和短路求值
逻辑运算符: 运算符 含义 优先级 ! 逻辑非 高 && 逻辑与 中 || 逻辑或 低 举例: !a:如果 a 为真,!a 为假:如果 a 为 假,!a 为真 a && ...
