NOI2011 Day2

NOI2011 Day2

道路修建

题目描述：给出一棵树，求每条边的两边的端点数的差乘边权之和。

solution：
题目可能描述得不太清楚，如图：

对于虚边，如果边权为10，两边的端点数之差为2，这条边对答案的贡献为20.
所以这道题就是求子树点数。

时间复杂度：\(O(n)\)

NOI嘉年华

题目描述：给出\(n\)个活动，每个活动有起始时间和终止时间，把这\(n\)个活动分在两个会场进行（也可以不举行某些活动），每个会场的活动的时间段可以相交，两个会场的活动的时间段不可以有交集。求活动较少的会场的活动最大值，以及在第\(i\)个活动一定要举行的情况下，活动较少的会场的活动最大值。

solution：
因为有两个会场，所以其中一个会场的活动数通过枚举，再求另一个会场的活动最大值会比较方便。
设\(f[i][j]\)表示到\(i\)时刻，A会场有\(j\)个活动，B会场活动数的最大值。\(sum(i, j)\)为时刻\(i\)到时刻\(j\)所包含的活动数。那么：

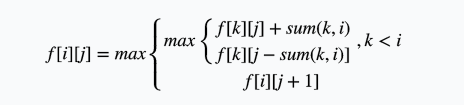
第一问的答案就是

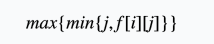
设\(g[i][j]\)表示在第\(i\)时刻后，A会场有\(j\)个活动，B会场活动数的最大值。那么：

设\(\varphi [i][j]\)表示时刻\(i\)到时刻\(j\)包含的活动一定要举行，活动较少的会场的活动最大值。那么：

对于每一个活动，设起始时间为\(L_i\), 终止时间为\(R_i\)，那么答案就是

对于固定的\(i, j\)，设

当\(x\)增大时，如果\(y\)也增大， 那么左式（逗号左面）会增大，右式（逗号右面）会减少，因为是取最小值，所以贡献不大。

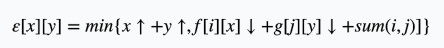
如果\(y\)减小，那么左式和右式都比较平衡，答案不会太差。

脑补……

时间复杂度：\(O(n^3)\)

兔兔与蛋蛋游戏

题目描述：这个游戏是在一个 n 行 m 列的棋盘上进行的。游戏开始之前，棋盘上有一个格子是空的，其它的格子中都放置了一枚棋子，棋子或者是黑色，或者是白色。
每一局游戏总是兔兔先操作，之后双方轮流操作，具体操作为：
1、兔兔每次操作时，选择一枚与空格相邻的白色棋子，将它移进空格。
2、蛋蛋每次操作时，选择一枚与空格相邻的黑色棋子，将它移进空格。
第一个不能按照规则操作的人输掉游戏。
给出一局兔兔输的操作过程，找出犯错的地方：在这次操作前兔兔有必胜策略，而这次操作后蛋蛋有必胜策略。

solution:

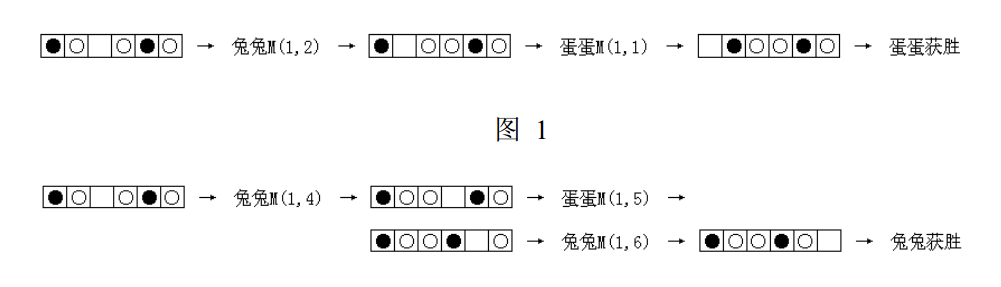
\(M(x, y)\)表示哪个棋移到空格。
从操作可以看出：
1、路径不能自交（从某一个点出发走回这个点需要偶数步，第一步的颜色与偶数步的颜色不同，所以不可能自交）
2、如果把初始空格看做黑棋，则路径为一条黑白相间的路径。
由性质二可以按黑棋和白棋构成二分图（黑左白右），相邻的黑棋与白棋连边。

判断兔兔的某一步是否必胜，则需判断这一步的黑棋对应的点是否一定在最大匹配中，如果是，则必胜，否则必败。

如图\(O\)一定在最大匹配中，那么从\(O\)出发，一定是实虚相间的边，实边为匹配边，一定存在，而右边的点不一定有虚边回到左边，所以必胜。
如果像\(P\)一样不一定在最大匹配中，那么\(P\)会经虚边走到右边，而从右边一定会有实边走回左边，虚边不一定有，所以必败。

判断蛋蛋的某一步是否必胜，则需判断这一步的白棋对应的点是否能到达黑棋的一个必败态，如果是，则必胜，否则必败。
所以只要判断与该白棋相连的黑棋是否必胜即可。

判断某点是否在最大匹配中，只需做一次最大匹配，然后把该点删掉，再做一次最大匹配，判断两次的最大匹配是否相等即可。

因为每次只删一个点，所以只要重新匹配这个点相连的那个点就好了，不要再做一次最大匹配。

时间复杂度：\(O(knm)\)