随手练——P1141 01迷宫

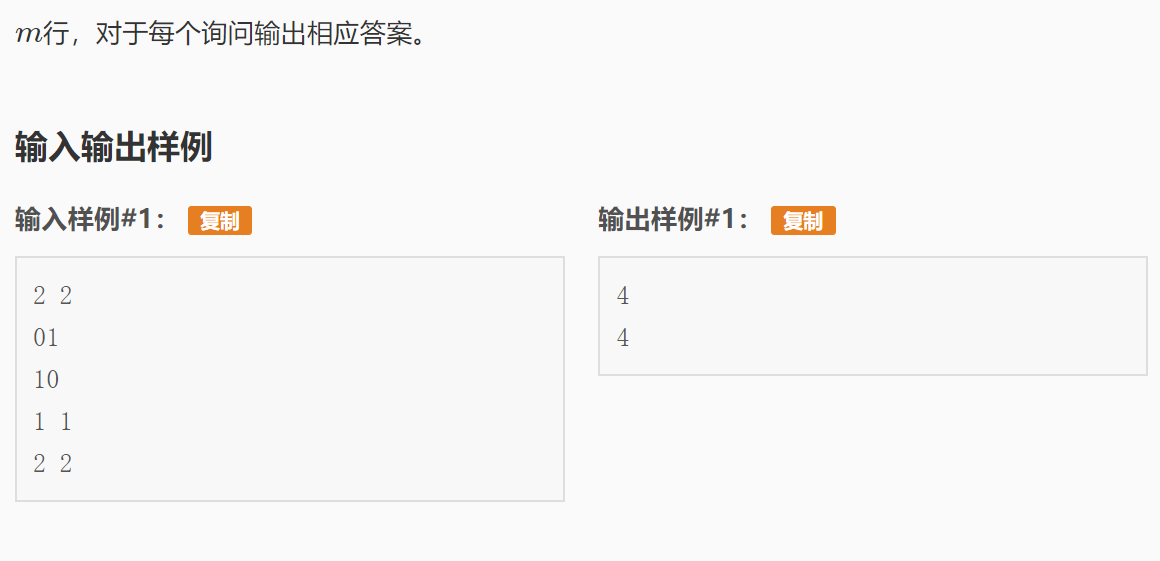
1、暴力版

本质上就是求连通块数量，那么DFS或者BFS都行，暴力跑。

写完发现题目比较特殊，m次提问，那每次都暴力搜，肯定是要跑死了。

#include <iostream>
#include <string.h>
#include <stdio.h>

int cnt,n;
int dir[][] = { {,},{-,},{,},{,-} };
bool fuck[][];
char s[][];

void dfs(int x, int y) {
    for (int k = ; k < ; k++) {
        int tox = x + dir[k][], toy = y + dir[k][];
        if (!fuck[tox][toy] && s[x][y] != s[tox][toy] && (tox >=  && tox < n && toy >=  && toy < n)) {
            cnt++;
            fuck[tox][toy] = true;
            dfs(tox, toy);
        }
    }
}
int main()
{
    int t;
    scanf("%d%d", &n, &t);
    for (int i = ; i < n; i++)scanf("%s", s[i]);

    int i, j;
    while (t--) {
        int c1, c2;
        memset(fuck, , sizeof(fuck));
        cnt = ;
        scanf("%d%d",&c1,&c2);
        fuck[c1 - ][c2 - ] = true;
        dfs(c1 - , c2 - );
        printf("%d\n", cnt);
    }
    return ;
}

2、改进版

要确定：每个联通区域的答案是一样的，就好办了。

核心代码：

void dfs(int x, int y,int d) {
    for (int k = ; k < ; k++) {
        int tox = x + dir[k][], toy = y + dir[k][];
        if (!fuck[tox][toy] && s[x][y] != s[tox][toy] && (tox >=  && tox < n && toy >=  && toy < n)) {
            cnt++;
            fuck[tox][toy] = d;
            dfs(tox, toy, d);
        }
    }
}

for (int i = ; i < n; i++) {
        for (int j = ; j < n; j++) {
            if (!fuck[i][j]) {
                fuck[i][j] = d;//d表示第几个连通区域
                cnt = ;
                dfs(i, j, d);
                ans[d++] = cnt;
            }
        }
    }

算是比较特殊的一种打表吧。

#include <iostream>
#include <string.h>
#include <stdio.h>

int cnt,n;
int dir[][] = { {,},{-,},{,},{,-} };
int fuck[][];
int ans[];
char s[][];

void dfs(int x, int y,int d) {
    for (int k = ; k < ; k++) {
        int tox = x + dir[k][], toy = y + dir[k][];
        if (!fuck[tox][toy] && s[x][y] != s[tox][toy] && (tox >=  && tox < n && toy >=  && toy < n)) {
            cnt++;
            fuck[tox][toy] = d;
            dfs(tox, toy, d);
        }
    }
}
int main()
{
    int t;
    scanf("%d%d", &n, &t);
    for (int i = ; i < n; i++)scanf("%s", s[i]);

    int i, j, d = ;
    for (int i = ; i < n; i++) {
        for (int j = ; j < n; j++) {
            if (!fuck[i][j]) {
                fuck[i][j] = d;
                cnt = ;
                dfs(i, j, d);
                ans[d++] = cnt;
            }
        }
    }

    while (t--) {
        int c1, c2;
        scanf("%d%d",&c1,&c2);
        printf("%d\n", ans[fuck[c1 - ][c2 - ]]);
    }
    return ;
}