KMP算法next数组求解

关于KMP算法，许多教材用的是递推式求解，虽然代码简洁，但是有些不好理解，这里我介绍一种迭代求next数组的方法

KMP算法关键部分就是滑动模式串，我们可以每次滑动一个单位，直到出现可能匹配的情况，此时失配处next数组的值，就是失配处当前对应的元素下标

如下图，在X处失配，则向右滑动1个单位，可见这种情况是明显不可能匹配的，于是再滑，一直滑到可能出现匹配情况为止，“C”与“？”可能是匹配的，故应停止在此处，故失配处next数组的值就是“C”所在下标

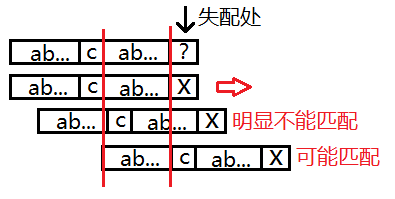
基于上述思路的代码如下：

#include<stdio.h>
#include<string.h>

void GetNext(char *str, int *arr);

void main()
{
    char str[] = "abaabacaba";
    int next[];

    GetNext(str, next);
    //结果：-1 0 0 1 1 2 3 0 1 2
}

void GetNext(char *str, int *arr)
{
    int i, j, k, flag, len = strlen(str);

    //整体思路
    //从失配处每次向右滑动一个单位，一直滑到可能匹配上的位置则停止
    //即滑动串与失配处之前的串的相应部分再次一一匹配
    for (i = , arr[] = -; i < len; i++)
    {
        //i表示next数组下标，即失配处序号
        for (j = ; j <= i; j++)
        {
            //j表示模式串向右滑动次数
            for (k = , flag = ; k < i - j; k++)
            {
                //k表示滑动后模式串的子串
                if (str[k] != str[k + j])
                {
                    flag = ;
                    break;
                }
            }
            if (flag ==  || j == i)
            {
                arr[i] = i - j;
                break;
            }
        }
    }
}

这个方法虽然没有递推式那么高效，但是整体还是比较好理解的，而且模式串一般不会太长，这种方法也不会花费太多时间就能得出next数组。

另外用php实现完整的kmp算法，这次用已知的next[x]（x < i）求未知的next[i]，并且next[i]定义为从0~i都是匹配的，即在i+1处才失配：

<?php

function getNext(string $pattern)
{
    $next = [];
    if (empty($pattern)) {
        return $next;
    } else {
        $next[0] = -1;
        for ($i = 1; $i < strlen($pattern) - 1; $i++) {
            $k = $next[$i - 1];
            if ($k == -1) {
                $next[$i] = $pattern[$k + 1] == $pattern[$i] ? 0 : -1;
            } else {
                while ($k > -1) {
                    if ($pattern[$k + 1] == $pattern[$i]) {
                        $next[$i] = $k + 1;
                        break;
                    }
                    $k = $next[$k];
                }
                $next[$i] = -1;
            }
        }
    }
    return $next;
}

function kmp(string $pattern, string $string)
{
    $next = getNext($pattern);
    if (empty($next)) {
        return false;
    }
    for ($i = 0, $j = -1; $i < strlen($string);) {
        if ($j + 1 == strlen($pattern)) {
            return $i - $j - 1;
        }
        if ($string[$i] == $pattern[$j + 1]) {
            $i++;
            $j++;
        } else {
            if ($j != -1) {
                $j = $next[$j];
            } else {
                $i++;
            }
        }
    }
    return false;
}